Содержание
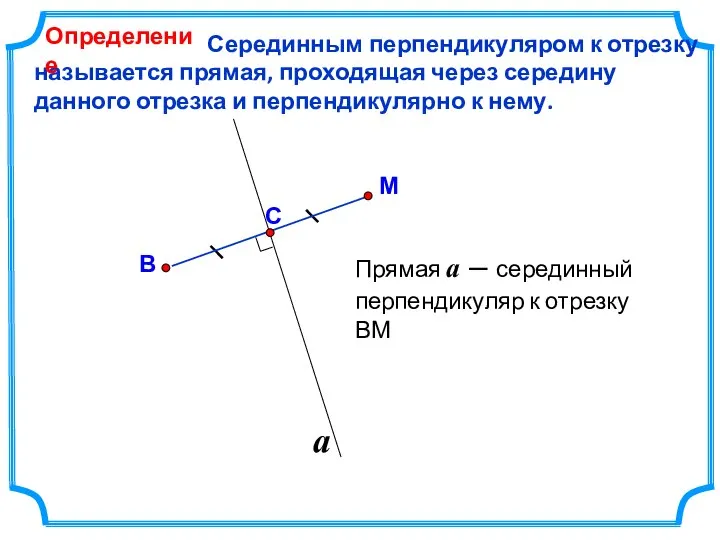
- 2. Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярно к нему. М
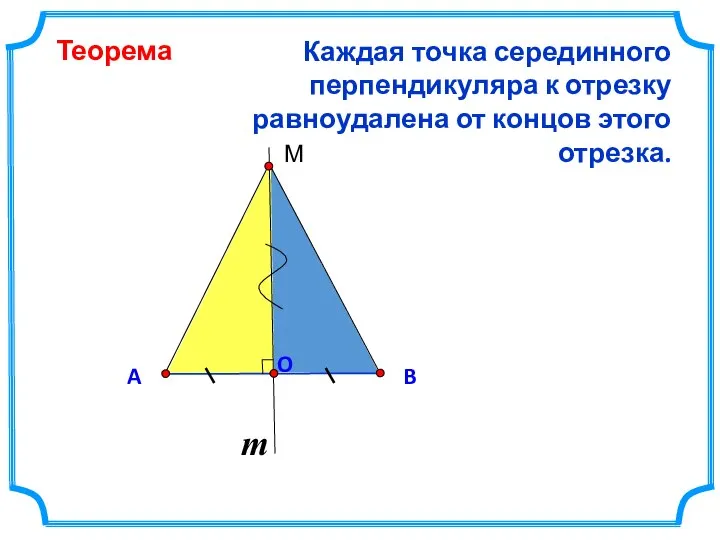
- 3. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. B A Теорема
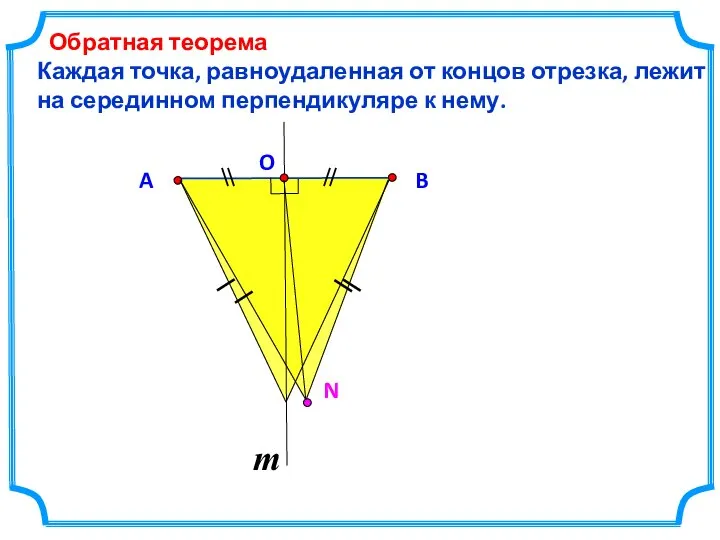
- 4. Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему. Обратная теорема
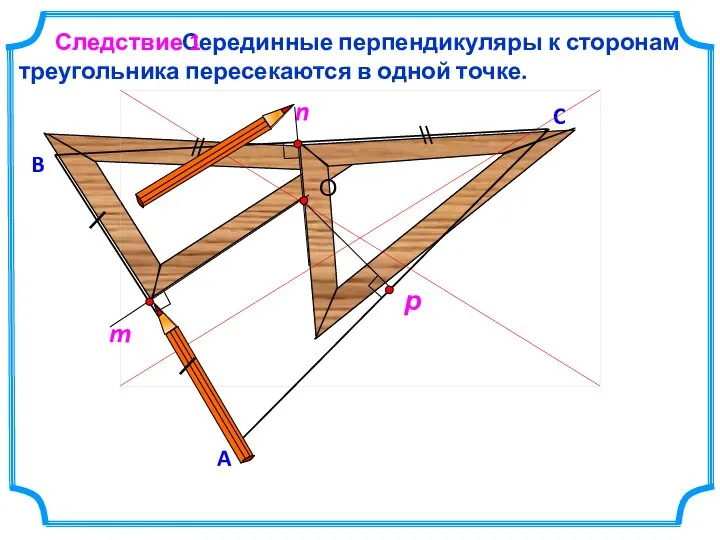
- 5. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. C B Следствие 1 A
- 6. Геометрическим местом точек плоскости, равноудаленных от концов отрезка, является серединный перпендикуляр к этому отрезку. Следствие 2
- 8. Скачать презентацию

 Старинные задачи на дроби
Старинные задачи на дроби Функция y=kx2, её свойства и график
Функция y=kx2, её свойства и график Производные функции нескольких переменных (часть 1)
Производные функции нескольких переменных (часть 1) Многочлены от нескольких переменных
Многочлены от нескольких переменных Статистический анализ зависимостей между гидрологическими переменными (лекция 11)
Статистический анализ зависимостей между гидрологическими переменными (лекция 11) Показательные уравнения
Показательные уравнения Геометрические фигуры
Геометрические фигуры Решение задач
Решение задач Презентация на тему Формулы приведения
Презентация на тему Формулы приведения  Пересекающиеся прямые
Пересекающиеся прямые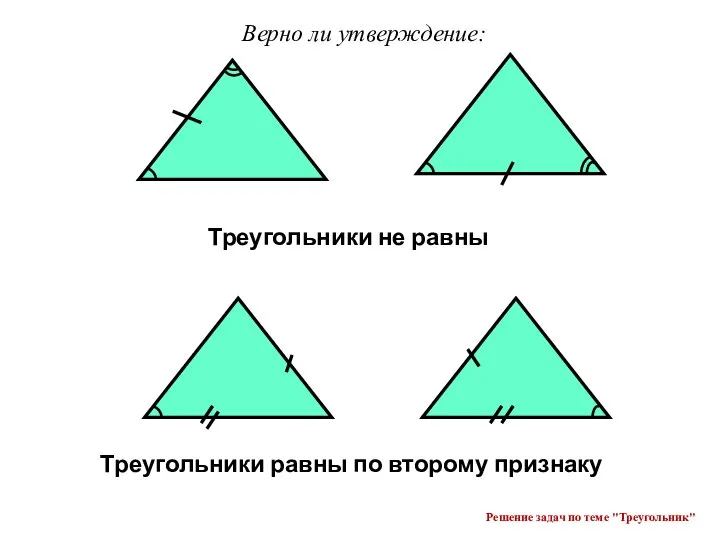 Решение задач по теме Треугольник
Решение задач по теме Треугольник Преобразование логарифмических выражений
Преобразование логарифмических выражений Параметрические характеристики параболы
Параметрические характеристики параболы Формулы для радиусов вписанной и описанной окружностей треугольника
Формулы для радиусов вписанной и описанной окружностей треугольника Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений Подготовка к ЕГЭ. Графическое решение уравнений и неравенств
Подготовка к ЕГЭ. Графическое решение уравнений и неравенств Нахождение производных функций
Нахождение производных функций Решение задач на проценты. Повторение, обобщение
Решение задач на проценты. Повторение, обобщение Тест по математике! Начнём. Сокращать дроби!
Тест по математике! Начнём. Сокращать дроби! Векторы в пространстве
Векторы в пространстве Средние значения в статистике
Средние значения в статистике Вычисление определенных интегралов с помощью неопределенных
Вычисление определенных интегралов с помощью неопределенных Презентация на тему Признаки делимости
Презентация на тему Признаки делимости  Операции с числовыми множествами. Формулы сокращённого умножения
Операции с числовыми множествами. Формулы сокращённого умножения Презентация на тему Понятие площади и объёма
Презентация на тему Понятие площади и объёма  Восстанови ряд чисел
Восстанови ряд чисел Численное интегрирование
Численное интегрирование Задачи на смеси и сплавы
Задачи на смеси и сплавы