Содержание
- 2. Устная работа Является ли алгебраической дробью выражения: можно представить как многочлен является алгебраической дробью является алгебраической
- 3. Устная работа Какую дробь называют алгебраической? Какие значения называют допустимыми значениями дроби?
- 4. Примеры алгебраических дробей: Повторим Алгебраическая дробь
- 5. Иногда алгебраическое выражение по форме является – алгебраической дробью, а по существу – нет. Например:
- 6. Решение Вывод: нельзя найти значение данной дроби при переменной х = 2 и при у =
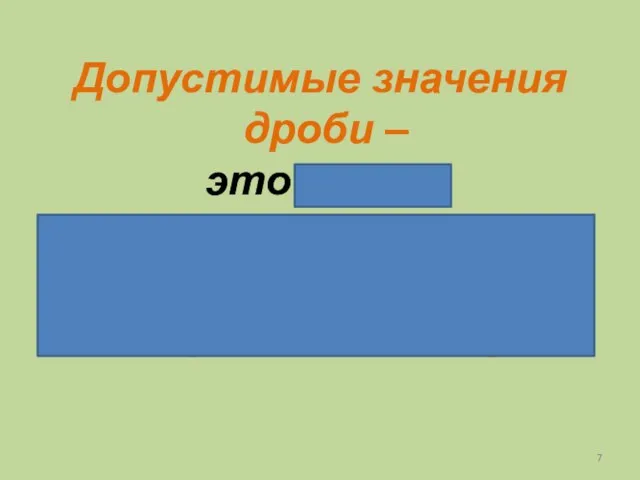
- 7. Допустимые значения дроби – это такие значения, при которых знаменатель дроби не обращается в нуль.
- 8. Допустимые значения дроби – это такие значения, при которых знаменатель дроби не обращается в нуль.
- 9. Алгоритм нахождения допустимых значений дроби: Находят значение переменной, при которых знаменатель дроби обращается в нуль. 2.
- 10. Алгоритм нахождения допустимых значений дроби: Находят значение переменной, при которых знаменатель дроби обращается в нуль. 2.
- 11. Установите, при каких значениях переменной не имеет смысла алгебраическая дробь: Решение (3t - 2)(3t + 2)
- 12. Установите, при каких значениях переменной не имеет смысла алгебраическая дробь: Решение Ответ: при а = -5.
- 13. Установите, при каких значениях переменной не имеет смысла алгебраическая дробь: Решение Ответ: при d = 41
- 14. Найдите значение переменной, при которых равна нулю алгебраическая дробь: равно 0, если х - 4 =
- 15. Учебные задания 1. Найти значение алгебраической дроби при х=-2 . 2. Укажите значение переменной, при котором
- 16. 20.06.2011 Кравченко Г. М.
- 18. Скачать презентацию













 Неравенства. Практическая работа №3
Неравенства. Практическая работа №3 Пропорции
Пропорции Преобразование функций и действия над ними
Преобразование функций и действия над ними Представление чисел с плавающей запятой
Представление чисел с плавающей запятой Вычислите устно. Задания
Вычислите устно. Задания Презентация на тему Такая разная геометрия
Презентация на тему Такая разная геометрия  Блиц-турнир по математике
Блиц-турнир по математике Случаи вычитания 12 -
Случаи вычитания 12 - Решение задач. 7 класс
Решение задач. 7 класс Число Пи вокруг нас
Число Пи вокруг нас Смежные и вертикальные углы
Смежные и вертикальные углы Решение систем уравнений графическим и аналитическим способом
Решение систем уравнений графическим и аналитическим способом chislo-pi
chislo-pi Икосаэдр
Икосаэдр Обыкновенные дроби
Обыкновенные дроби Сечение куба, призмы, пирамиды
Сечение куба, призмы, пирамиды Сложение и вычитание дробей
Сложение и вычитание дробей Дистанционный конкурс Царство ребусов
Дистанционный конкурс Царство ребусов Игры разума. Физико-математическая игра для учащихся 8 классов
Игры разума. Физико-математическая игра для учащихся 8 классов Вычисление производной степенной функции. Правила дифференцирования. Производные суммы, разности, произведения, частного
Вычисление производной степенной функции. Правила дифференцирования. Производные суммы, разности, произведения, частного Презентация на тему Куб
Презентация на тему Куб  Абсолютная величина вектора в пространстве
Абсолютная величина вектора в пространстве Презентация на тему Доли. Обыкновенные дроби (5 класс)
Презентация на тему Доли. Обыкновенные дроби (5 класс)  Riešenie rovníc, ak je neznáma na oboch stranách rovnice
Riešenie rovníc, ak je neznáma na oboch stranách rovnice Понятие о проценте
Понятие о проценте Чему научились во 2 классе
Чему научились во 2 классе Теорема Пифагора
Теорема Пифагора Презентация на тему Дециметр (1 класс)
Презентация на тему Дециметр (1 класс)