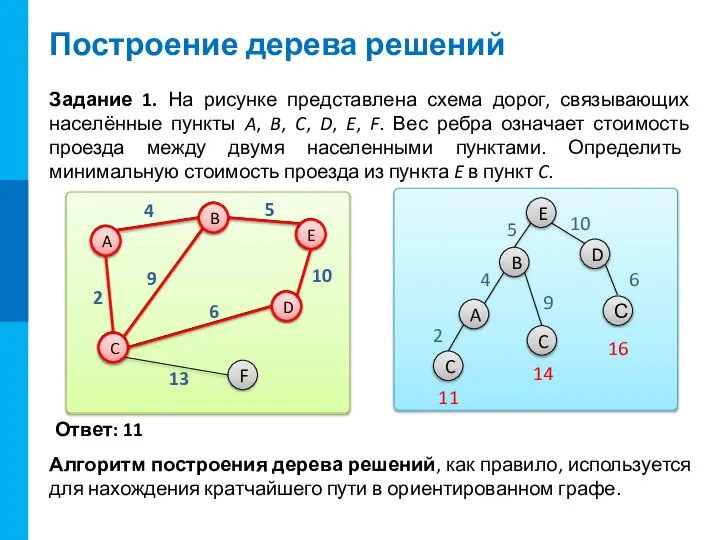
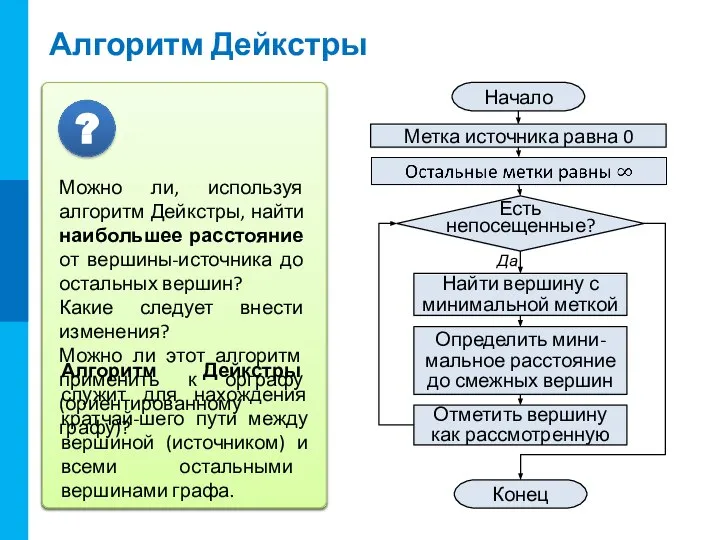
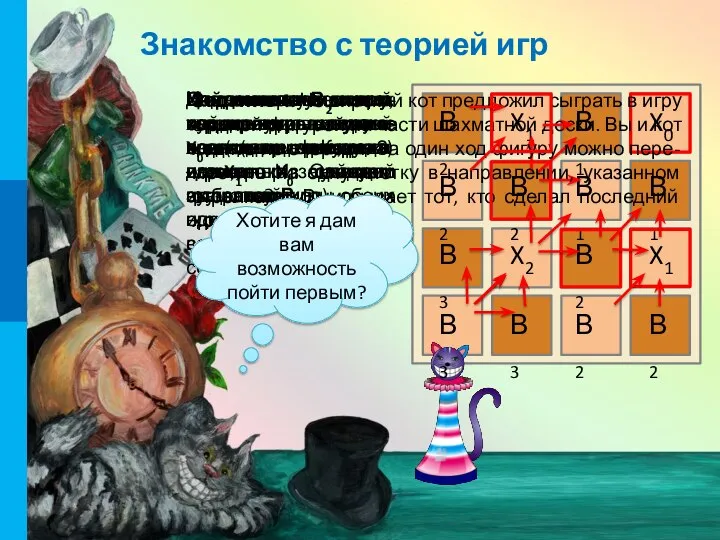
одной фигурой на части шахматной доски. Вы и кот ходите по очереди. За один ход фигуру можно пере-местить на одну клетку в направлении, указанном стрелками. Выигрывает тот, кто сделал последний ход.
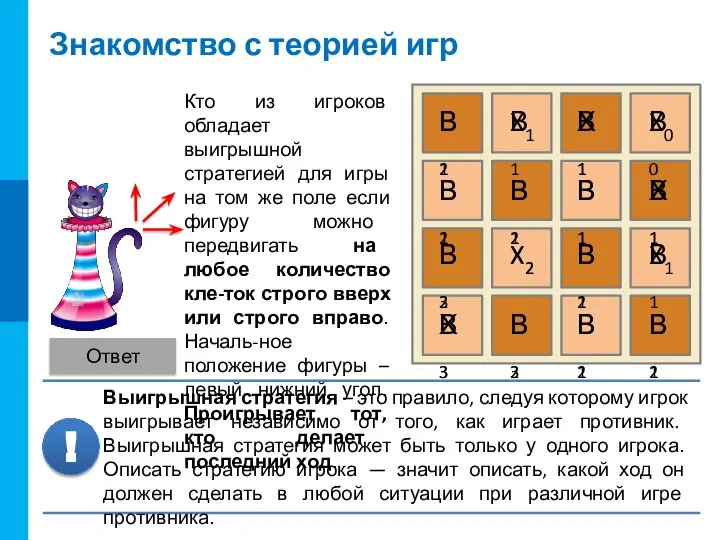
Найдем такую клетку, ход в которую означает выигрыш для игрока, занявшего эту позицию, и проигрыш для соперника.
Отметим эту клетку как проигрышную – X0 (для того, кто должен сейчас выполнять ход).
Индекс означает коли-чество ходов из этой позиции до развязки игры.
Найдем клетки, из ко-торых можно поставить фигуру в позицию X0. Отметим их знаком В1.
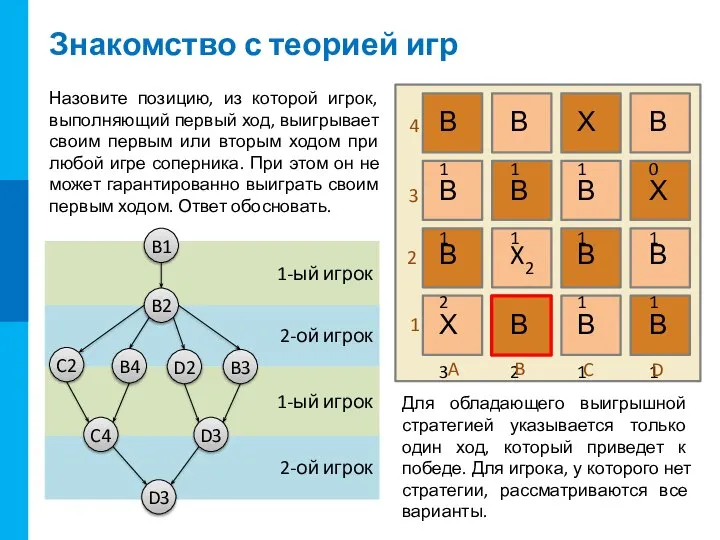
Для четырех позиций определено возможное развитие игры, при условии грамотной игры обоих игроков.
Из отмеченных клеток существует только один вариант хода игрока.
Клетки являются про-игрышными в один ход (ходящего игрока) – X1. Из каждой существует единственный вариант развития событий.
Из клеток можно пойти в три различные клетки. Какие варианты следует выбрать?
Метки клеток В2.
Хотите я дам вам возможность пойти первым?
В2
X2
В2
В3
В3
В3
В2
В2

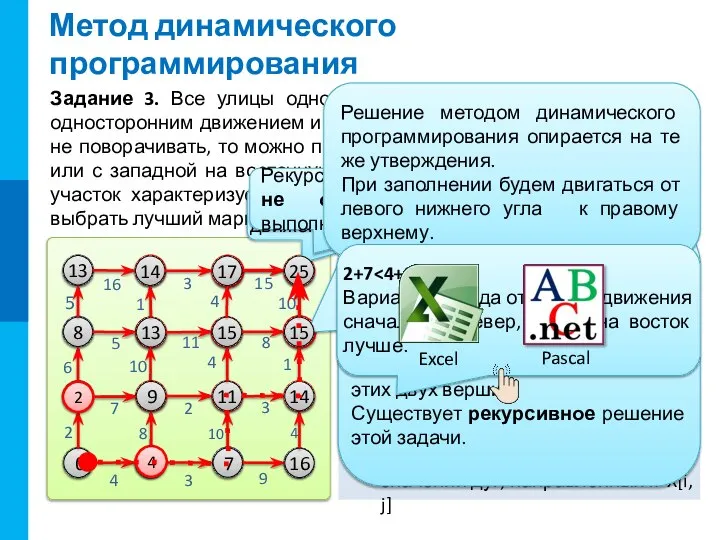
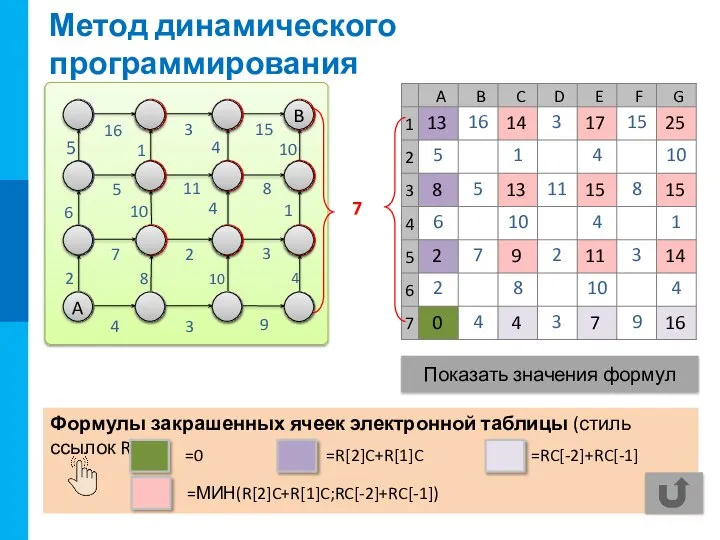
![Метод динамического программирования A 7 const n=7; var A: array [1..n, 1..n]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1020507/slide-7.jpg)




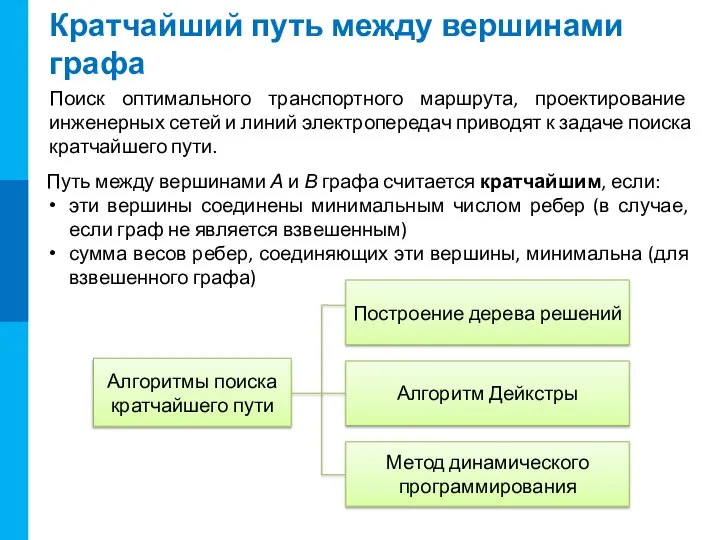
 Теорема Пифагора
Теорема Пифагора Классы интегрируемых функций
Классы интегрируемых функций Интеллектуальная игра по математике для 8 класса
Интеллектуальная игра по математике для 8 класса Движение в геометрии
Движение в геометрии Математическая модель
Математическая модель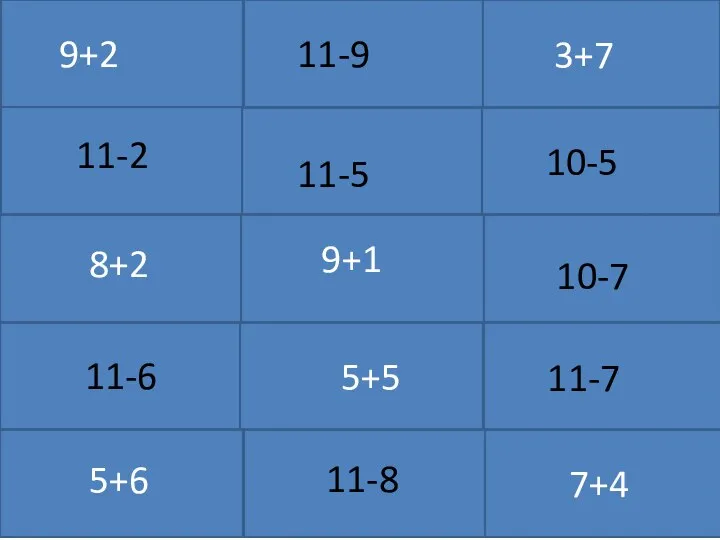 Примеры. Карточки, счет +-10, 11, 12
Примеры. Карточки, счет +-10, 11, 12 Анализ уравнения на соответствие графику
Анализ уравнения на соответствие графику Масса предметов
Масса предметов Теория игр
Теория игр Методика изучения площади
Методика изучения площади Элементы комбинаторики. Перестановки
Элементы комбинаторики. Перестановки Линейная зависимость и линейная независимость системы векторов. Семинар 4
Линейная зависимость и линейная независимость системы векторов. Семинар 4 Осевая семетрия
Осевая семетрия Координатная плоскость. Ордината. Абсцисса
Координатная плоскость. Ордината. Абсцисса Алгоритм и письменное деление на двузначное число
Алгоритм и письменное деление на двузначное число Темір жолдың жылжымалы құрамын пайдалану, жөндеу және техникалық қызмет көрсету (түрлері бойынша)
Темір жолдың жылжымалы құрамын пайдалану, жөндеу және техникалық қызмет көрсету (түрлері бойынша)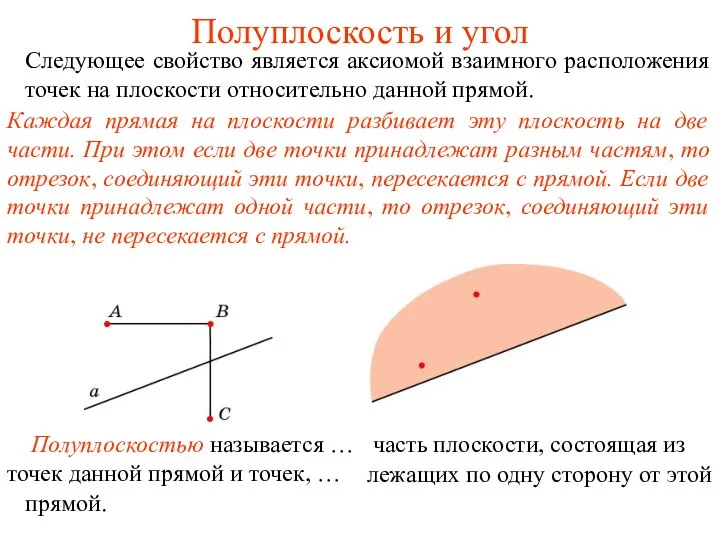 Полуплоскость и угол
Полуплоскость и угол Компланарны ли тройки векторов
Компланарны ли тройки векторов Четырехугольники
Четырехугольники Общее уравнение прямой и плоскости. Лекция1 (1)
Общее уравнение прямой и плоскости. Лекция1 (1) Математика интелектуальная разминка
Математика интелектуальная разминка Усеченый конус
Усеченый конус Кратчайшие расстояния
Кратчайшие расстояния Параллельные прямые 7 класс
Параллельные прямые 7 класс Таблица истинности
Таблица истинности Готфрид Лейбниц (1646 – 1716) – немецкий математик, физик, философ, юрист, языковед
Готфрид Лейбниц (1646 – 1716) – немецкий математик, физик, философ, юрист, языковед Таблицы данных с двумя переменными
Таблицы данных с двумя переменными Показательные уравнения и неравенства
Показательные уравнения и неравенства