- Главная
- Математика
- Арктангенс и арккотангенс

Содержание
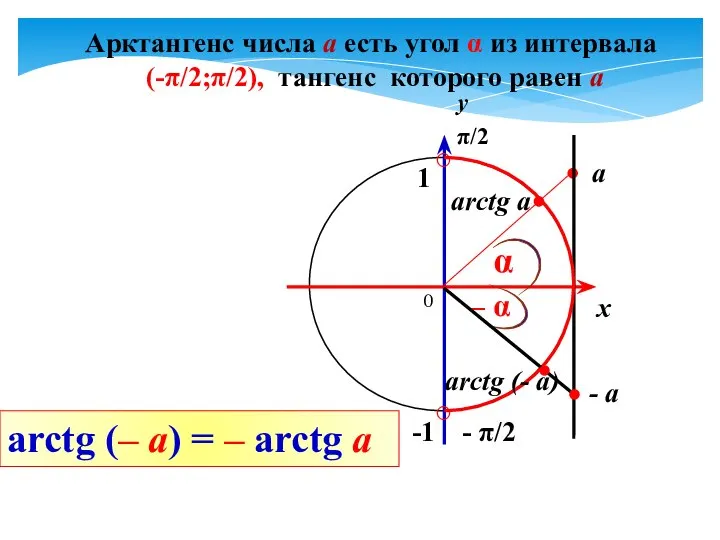
Слайд 2Арктангенс числа а есть угол α из интервала
(-π/2;π/2), тангенс которого равен
Арктангенс числа а есть угол α из интервала
(-π/2;π/2), тангенс которого равен
а
arctg a
а
π/2
- π/2
у
х
α
– α
- а
arctg (- a)
arctg (– a) = – arctg a
Слайд 30
Арккотангенс числа а есть угол
α из интервала (0; π),
котангенс которого
0
Арккотангенс числа а есть угол
α из интервала (0; π),
котангенс которого

равен а
а
arcctg (- a)
у
○
○
π
α
arcctg a
- а
arcctg (– a) = π – arcctg a
- Предыдущая
Настройка МФАСледующая -
Тема 1. Макроекономіка як наука Значение синуса, косинуса и тангенса для углов 30°, 45°, 60°
Значение синуса, косинуса и тангенса для углов 30°, 45°, 60° Решение составных задач
Решение составных задач Построение сечений параллелепипеда
Построение сечений параллелепипеда Задачи, обратные данной
Задачи, обратные данной Формулы двойного угла
Формулы двойного угла Аппроксимация функций. Метод Лагранжа
Аппроксимация функций. Метод Лагранжа Презентация на тему Решение экспериментальных задач
Презентация на тему Решение экспериментальных задач  Решение нелинейных уравнений
Решение нелинейных уравнений Арифметическая прогрессия. ОБОБЩАЮЩИЙ УРОК
Арифметическая прогрессия. ОБОБЩАЮЩИЙ УРОК Равносильность формул логики. Законы логики
Равносильность формул логики. Законы логики Решение задач на нахождение площади фигур. 6 класс
Решение задач на нахождение площади фигур. 6 класс Первообразная
Первообразная Углы, диаграммы, факториал. Повторение
Углы, диаграммы, факториал. Повторение Презентация по математике "Решение задач на разностное и кратное сравнение чисел" -
Презентация по математике "Решение задач на разностное и кратное сравнение чисел" -  Математическая задача
Математическая задача Дифференцирование оригинала, интегрирование оригинала, дифференцирование изображения, интегрирование изображения
Дифференцирование оригинала, интегрирование оригинала, дифференцирование изображения, интегрирование изображения Решето эратосфена
Решето эратосфена Веселая математика
Веселая математика Метод интервалов. Общий метод интервалов
Метод интервалов. Общий метод интервалов Решение заданий олимпиады ПРОФИ 2017
Решение заданий олимпиады ПРОФИ 2017 Скалярное произведение векторов
Скалярное произведение векторов Счёт до 8. Состав числа 8
Счёт до 8. Состав числа 8 Анализ геометрической формы предмета
Анализ геометрической формы предмета Страна геометрических фигур
Страна геометрических фигур Формулы приведения. Математический диктант
Формулы приведения. Математический диктант Угол – это фигура, образованная двумя лучами с общим началом
Угол – это фигура, образованная двумя лучами с общим началом Возрастание и убывание функций. Экстремумы
Возрастание и убывание функций. Экстремумы Площадь полной поверхности призмы
Площадь полной поверхности призмы