Содержание
- 2. Теорема о сложности сортировки
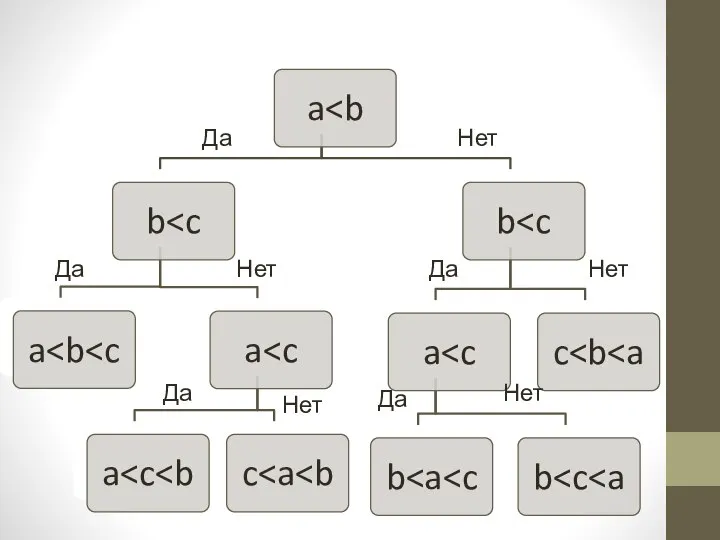
- 3. Да Нет Нет Нет Нет Нет Да Да Да Да
- 4. Теорема о сложности сортировки
- 5. Теорема о сложности сортировки
- 7. Для пересылок: если мы определили требуемую перестановку и имеем память для второй копии массива, то достаточно
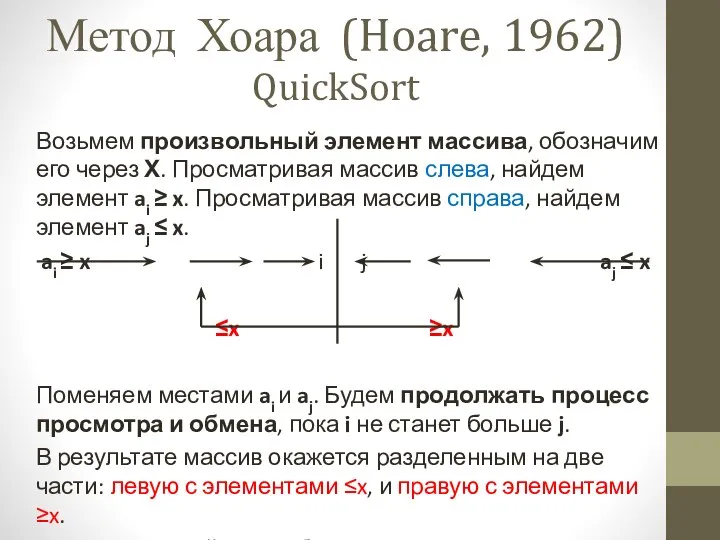
- 8. Возьмем произвольный элемент массива, обозначим его через Х. Просматривая массив слева, найдем элемент ai ≥ x.
- 9. Метод Хоара (QuickSort) Алгоритм на псевдокоде L, R – левая и правая границы рабочей части массива
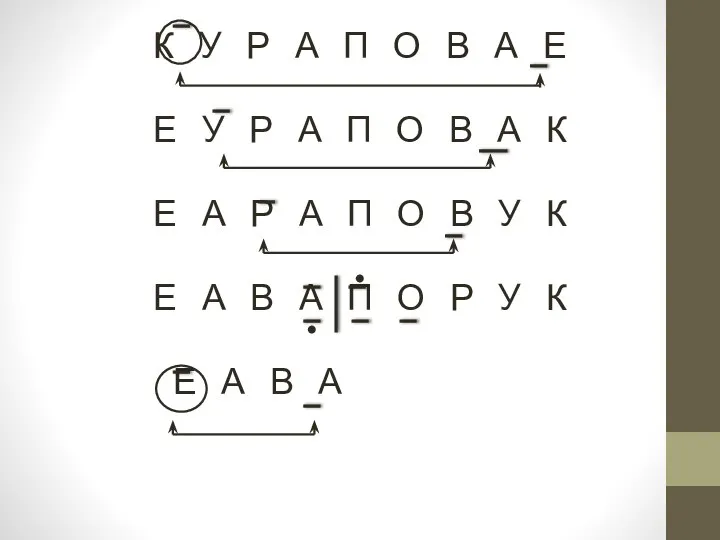
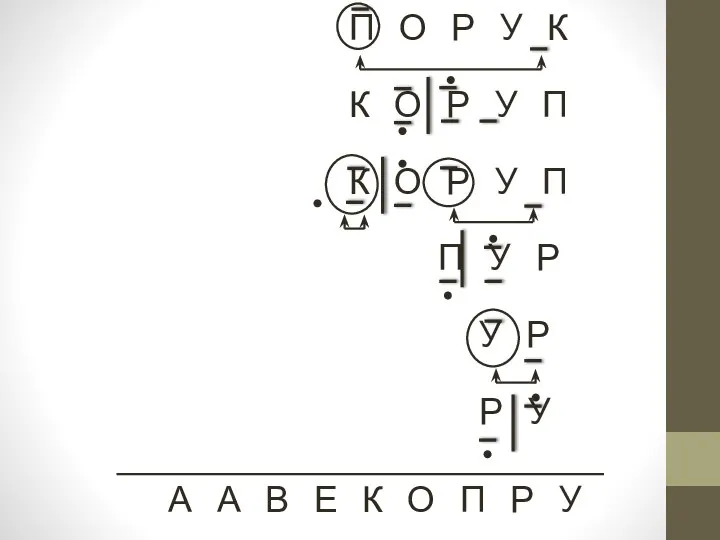
- 10. К У Р А П О В А Е Е У Р А П О В
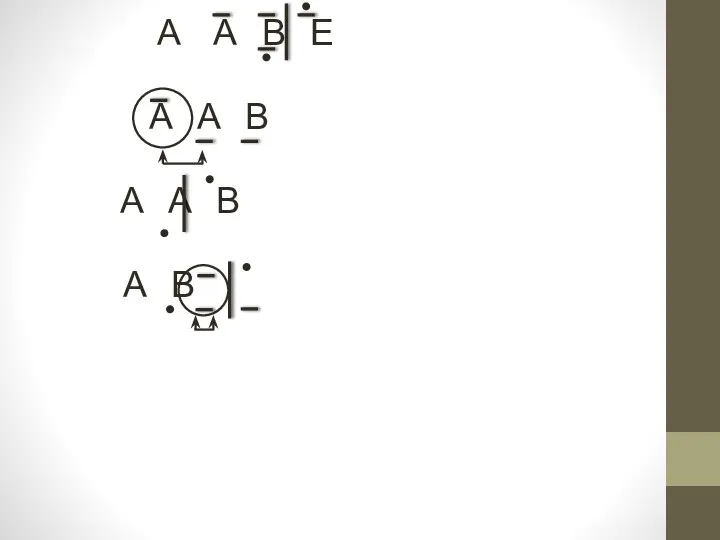
- 11. А А В Е А А В А А В А В
- 12. П О Р У К К О Р У П К О Р У П П
- 14. 2) Х = med (aL ,…, aR) – медиана Определение. Элемент am называется медианой для элементов
- 15. Пример. X Х Х Х Х Х Х
- 16. Итак, количество сравнений C = n log n Количество пересылок зависит от расположения элементов, но не
- 17. Проблема глубины рекурсии В теле подпрограммы доступны все объекты, описанные в основной программе, в том числе
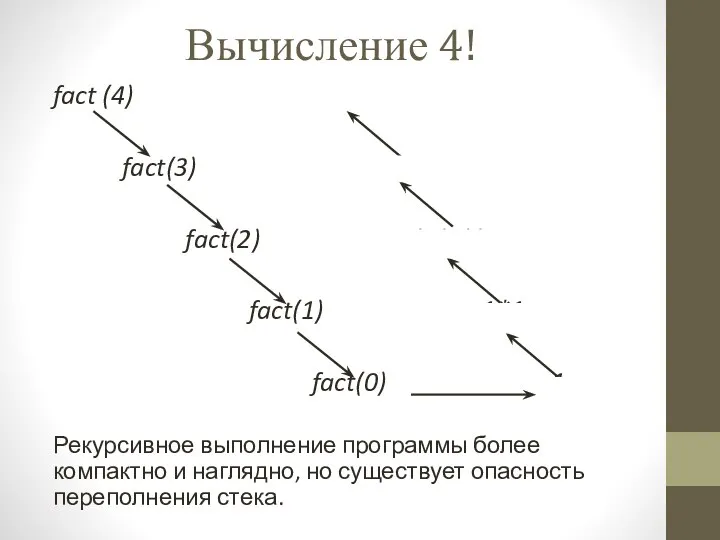
- 18. Вычисление 4! fact (4) (((1*1)*2)*3)*4 fact(3) ((1*1)*2)*3 fact(2) (1*1)*2 fact(1) 1*1 fact(0) 1 Рекурсивное выполнение программы
- 19. Фрейм: При выходе из подпрограммы эта память (фрейм) освобождается. Но если подпрограмма вызывает другую подпрограмму или
- 21. Вместо двух рекурсивных вызовов (для левой и правой части массива) будем использовать только один рекурсивный вызов,
- 23. Примеры рекурсии Преподаватель всегда прав. Если преподаватель не прав, смотри пункт 1. Бюрократия разрастается, чтобы удовлетворить
- 25. Скачать презентацию
















 Задачи на решение треугольника
Задачи на решение треугольника Решение выражений в несколько действий
Решение выражений в несколько действий Таблица умножения на 4
Таблица умножения на 4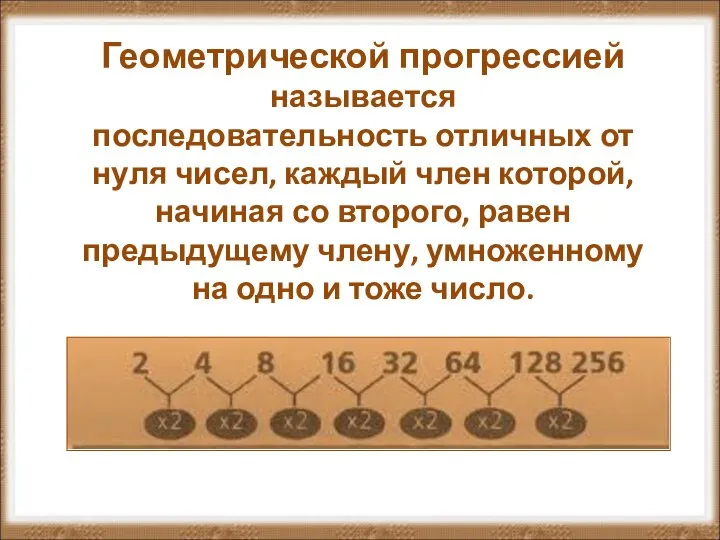 Возможности геометрической прогрессии в отношении растения одуванчик (часть 2)
Возможности геометрической прогрессии в отношении растения одуванчик (часть 2) Старинные системы мер
Старинные системы мер Математические модели электромеханических объектов управления
Математические модели электромеханических объектов управления 20140130_dekada
20140130_dekada Вычислительная математика. Практика №1
Вычислительная математика. Практика №1 Тема: Письменное умножение на двузначное число. Закрепление.
Тема: Письменное умножение на двузначное число. Закрепление. Взятие Измаила в математических и исторических нюансах
Взятие Измаила в математических и исторических нюансах Прямая на плоскости
Прямая на плоскости Электронные таблицы. Построение графиков и диаграмм
Электронные таблицы. Построение графиков и диаграмм Подготовка к ГИА. Демоверсия 2013
Подготовка к ГИА. Демоверсия 2013 Тригонометрия. Определение синуса, косинуса, тангенса и котангенса угла
Тригонометрия. Определение синуса, косинуса, тангенса и котангенса угла Параллельность прямых и плоскостей в пространстве
Параллельность прямых и плоскостей в пространстве Первый признак подобия треугольников. Решение задач
Первый признак подобия треугольников. Решение задач Ромб. Решение 6 задачи
Ромб. Решение 6 задачи Масса. Весы
Масса. Весы 08.09
08.09 Функции. Их свойства
Функции. Их свойства Формы графического изображения. (Лекция 3)
Формы графического изображения. (Лекция 3) Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика парні і непарні функції-1
парні і непарні функції-1 Личные (семейные) финансы. Финансовое планирование и бюджет. Решение задач
Личные (семейные) финансы. Финансовое планирование и бюджет. Решение задач Иррациональные уравнения
Иррациональные уравнения Методика ознакомления обучающихся с геометрическими фигурами (прямой, ломаной) и их свойствами
Методика ознакомления обучающихся с геометрическими фигурами (прямой, ломаной) и их свойствами Графы. Теория графов
Графы. Теория графов Конструктор (1)
Конструктор (1)