Содержание
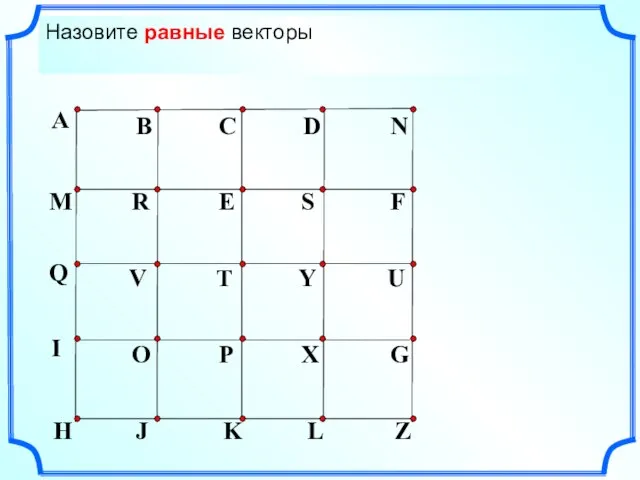
- 2. Назовите коллинеарные сонаправленные векторы Назовите коллинеарные противоположнонаправленные векторы Назовите равные векторы
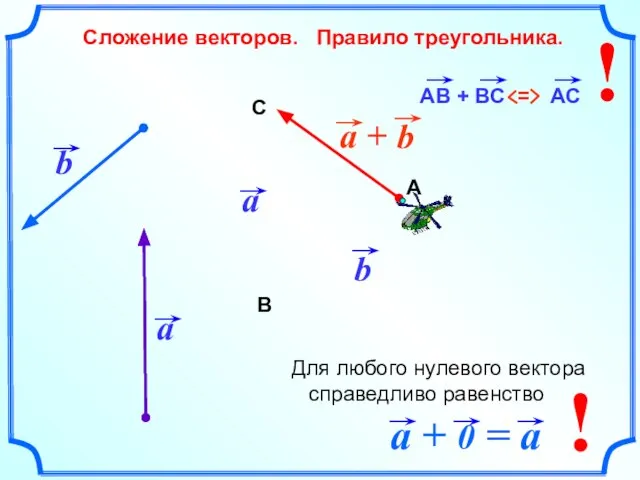
- 3. Сложение векторов. Правило треугольника. b А В С ! ! Для любого нулевого вектора справедливо равенство
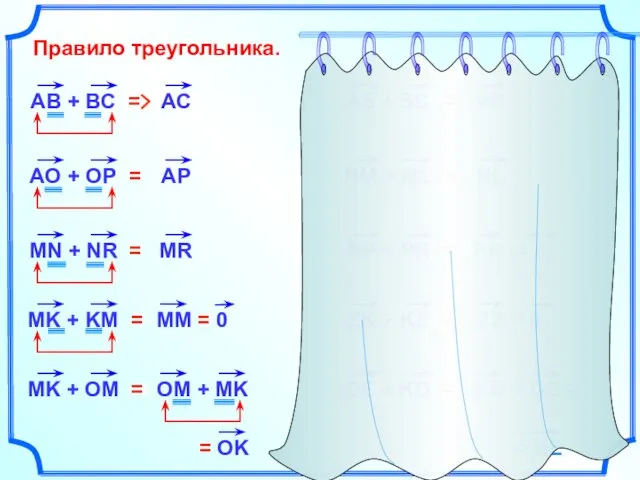
- 4. Правило треугольника. RR = 0
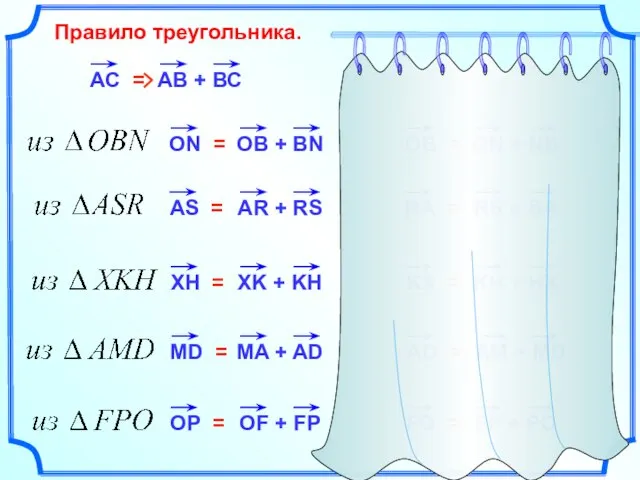
- 5. Правило треугольника. АС = OB = RA = KX = AD = FO =
- 6. Законы сложения векторов Для любых векторов справедливы равенства: 1 2 ! ! Теорема
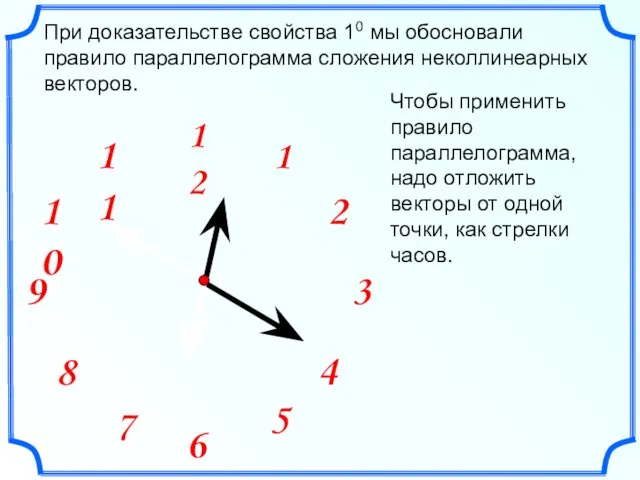
- 7. При доказательстве свойства 10 мы обосновали правило параллелограмма сложения неколлинеарных векторов. Чтобы применить правило параллелограмма, надо
- 8. Сложение векторов. Правило параллелограмма.
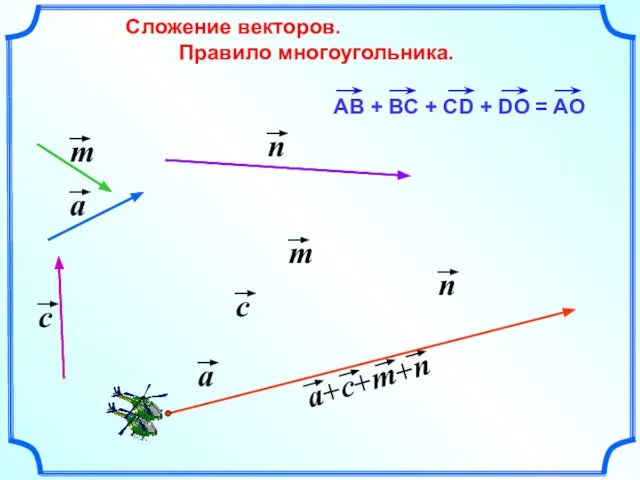
- 9. Сложение векторов. Правило многоугольника.
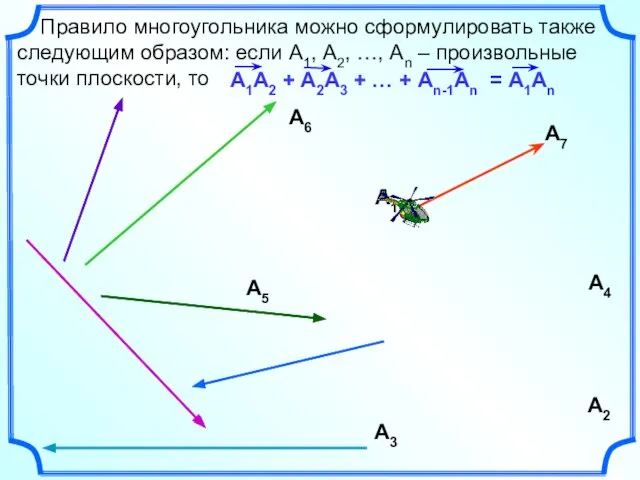
- 10. Правило многоугольника можно сформулировать также следующим образом: если А1, А2, …, Аn – произвольные точки плоскости,
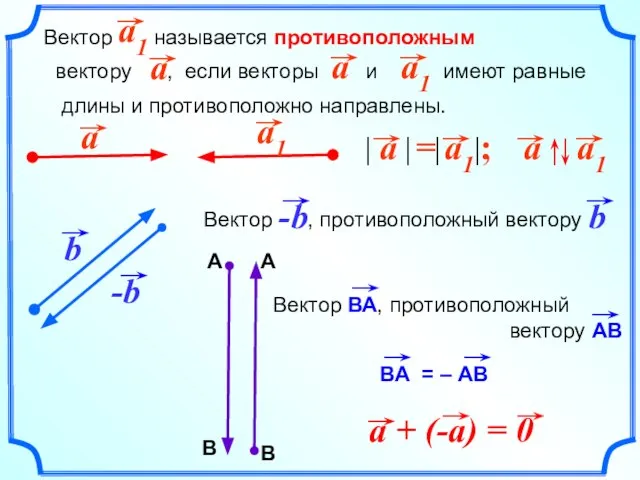
- 12. Вектор называется противоположным вектору , если векторы и имеют равные длины и противоположно направлены.
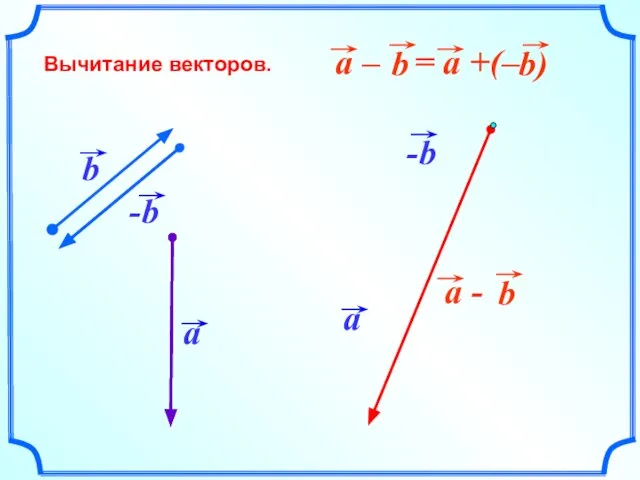
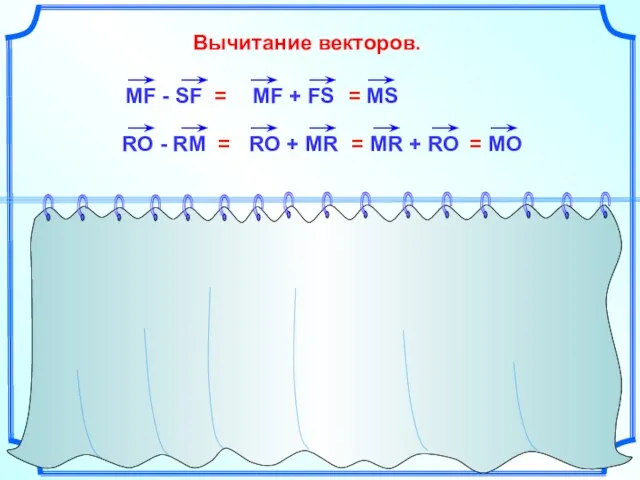
- 13. Вычитание векторов.
- 14. Вычитание векторов.
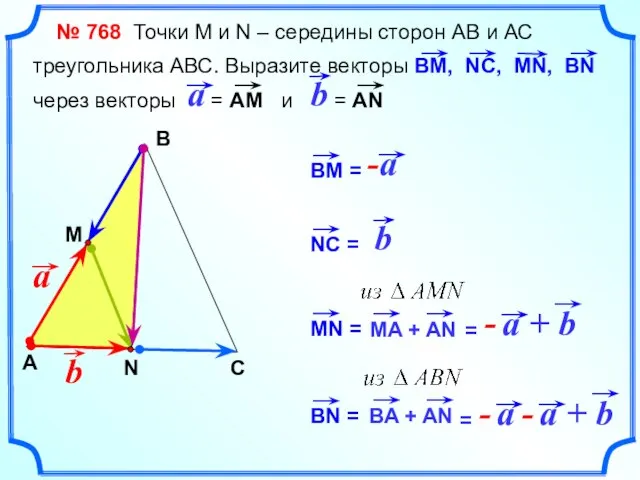
- 15. № 768 Точки М и N – середины сторон АВ и АС треугольника АВС. Выразите векторы
- 17. Скачать презентацию



 Прогрессия. Алгебраический анзац
Прогрессия. Алгебраический анзац Упрощение выражений. Решение задач
Упрощение выражений. Решение задач Статистическая теория радиотехнических систем. Корреляционный анализ детерминированных процессов. (Лекция 4)
Статистическая теория радиотехнических систем. Корреляционный анализ детерминированных процессов. (Лекция 4) Знаки тригонометрических функций. Формулы сложения
Знаки тригонометрических функций. Формулы сложения Мнимые числа. Определение комплексных чисел
Мнимые числа. Определение комплексных чисел Линейные неравенства с параметром
Линейные неравенства с параметром Понятие логарифма
Понятие логарифма Решение примеров
Решение примеров Основные результаты ЕГЭ по математике в 2021 году
Основные результаты ЕГЭ по математике в 2021 году Тест. Реши. И ты станешь уважать себя
Тест. Реши. И ты станешь уважать себя Симметрия. Виды симметрии
Симметрия. Виды симметрии Многоугольники в нашей жизни
Многоугольники в нашей жизни День таблицы умножения
День таблицы умножения Реляционная алгебра
Реляционная алгебра Построение графика функции, используя её свойства
Построение графика функции, используя её свойства Интерактивный тренажер Подобные слагаемые
Интерактивный тренажер Подобные слагаемые Таблица умножения числа 2 и на число 2
Таблица умножения числа 2 и на число 2 Презентация на тему Тригонометрические функции
Презентация на тему Тригонометрические функции  Иррациональные неравенства
Иррациональные неравенства Контрольная 2
Контрольная 2 Магические цифры
Магические цифры Подготовка к дифференцированному зачёту по математике. Нижегородский авиационный технический колледж
Подготовка к дифференцированному зачёту по математике. Нижегородский авиационный технический колледж Приемы решения целых уравнений
Приемы решения целых уравнений Презентация на тему Занимательная математика для детей (устный счёт + учимся писать цифры)
Презентация на тему Занимательная математика для детей (устный счёт + учимся писать цифры)  Презентация на тему Квадратный корень. Арифметический квадратный корень
Презентация на тему Квадратный корень. Арифметический квадратный корень  Математические методы решения задач по акустике волнового уравнения. Фундаментальные решения волновых уравнений
Математические методы решения задач по акустике волнового уравнения. Фундаментальные решения волновых уравнений РўР’РёРњРЎ_Лекция 2_Теоремы Рѕ вероятностях СЃРожных событий (4)
РўР’РёРњРЎ_Лекция 2_Теоремы Рѕ вероятностях СЃРожных событий (4) Объемы тел. Подготовка к контрольной работе
Объемы тел. Подготовка к контрольной работе