Бесконечно убывающая геометрическая прогрессия

Цель обучения:
применять формулу суммы бесконечно убывающей геометрической прогрессии для перевода десятичной периодической дроби в обыкновенную дробь.

Критерии оценивания:
Знает определение бесконечно убывающей геометрической прогрессии
Выводит формулу суммы бесконечно убывающей геометрической прогрессии

I. Арифметическая и геометрическая прогрессии. Вопросы
1. Определение арифметической прогрессии.
Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.
2. Формула n-го члена арифметической прогрессии.
3. Формула суммы первых n членов арифметической прогрессии .
4. Определение геометрической прогрессии.
Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число
5. Формула n-го члена геометрической прогрессии.
6. Формула суммы первых n членов геометрической прогрессии .

II. Арифметическая прогрессия.
Задания
Арифметическая прогрессия задана формулой an = 7 – 4n Найдите a10.
(-33)
2. В арифметической прогрессии a3 = 7 и a5 = 1.
Найдите a4 .
(4)
3. В арифметической прогрессии a3 = 7 и a5 = 1.
Найдите a17.
(-35)
4. В арифметической прогрессии a3 = 7 и a5 = 1.
Найдите S17.
(-187)

II. Геометрическая прогрессия.
Задания
5. Для геометрической прогрессии
найдите пятый член
6. Для геометрической прогрессии
найдите n-й член.
7. В геометрической прогрессии b3 = 8 и b5 = 2.
Найдите b4.
(4)
8. В геометрической прогрессии b3 = 8 и b5 = 2.
Найдите b1 и q.
9. В геометрической прогрессии b3 = 8 и b5 = 2.
Найдите S5.
(62)

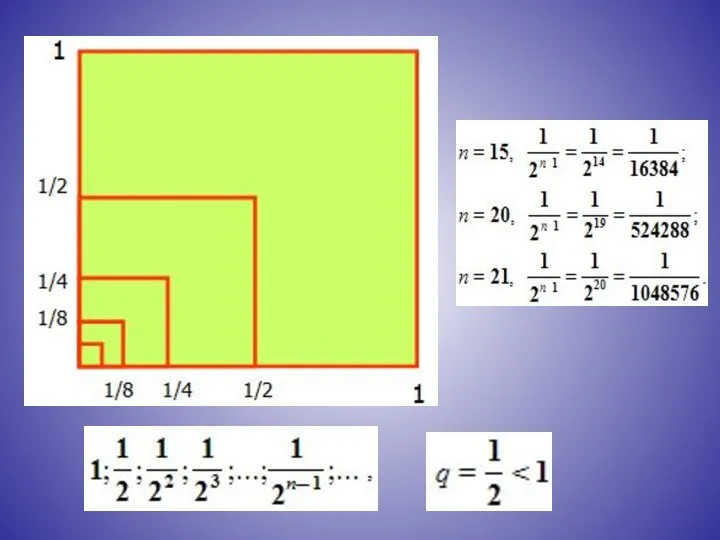
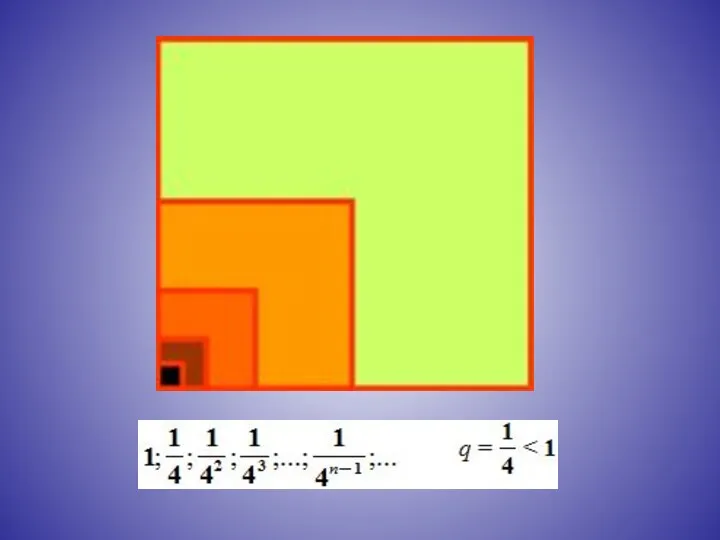
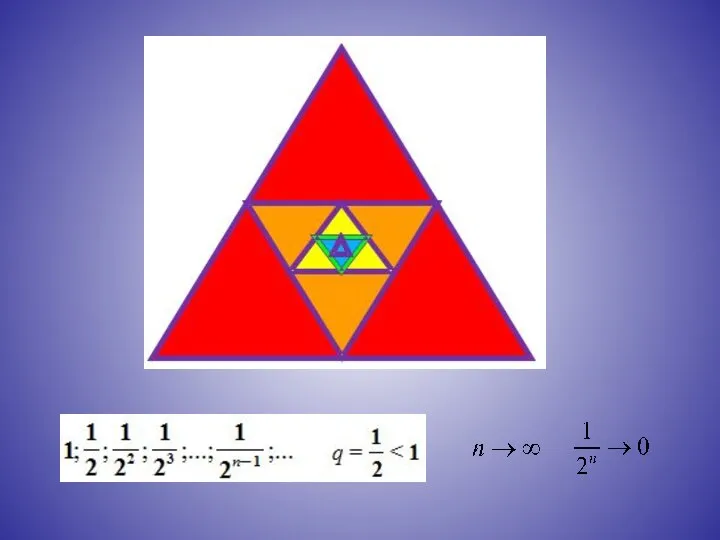
определение:
Геометрическая прогрессия называется
бесконечно убывающей, если модуль её
знаменателя меньше единицы.

Задача №1
Является ли последовательность бесконечно убывающей геометрической прогрессией, если она задана формулой:
Решение: а)
данная геометрическая прогрессия является бесконечно убывающей.
б)
данная последовательность не является бесконечно убывающей
геометрической прогрессией.

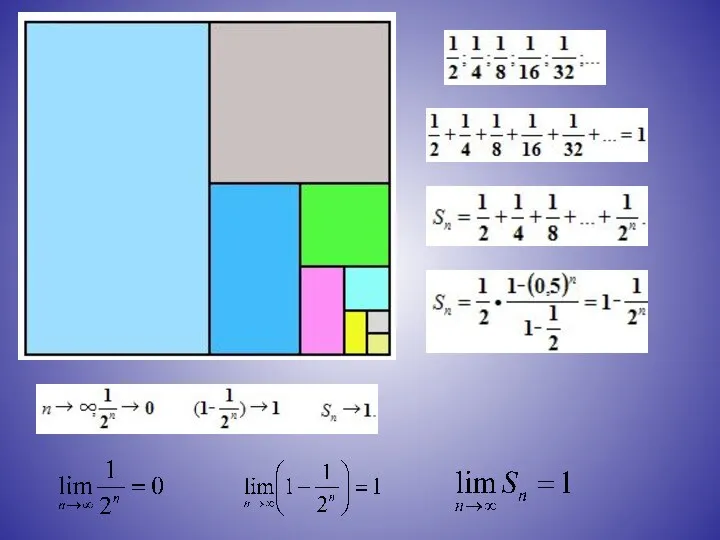
Сумма бесконечно убывающей геометрической прогрессии есть предел последовательности S1, S2, S3, …, Sn, … .
Например, для прогрессии
имеем
Так как
Сумму бесконечно убывающей геометрической прогрессии можно находить по формуле