Содержание
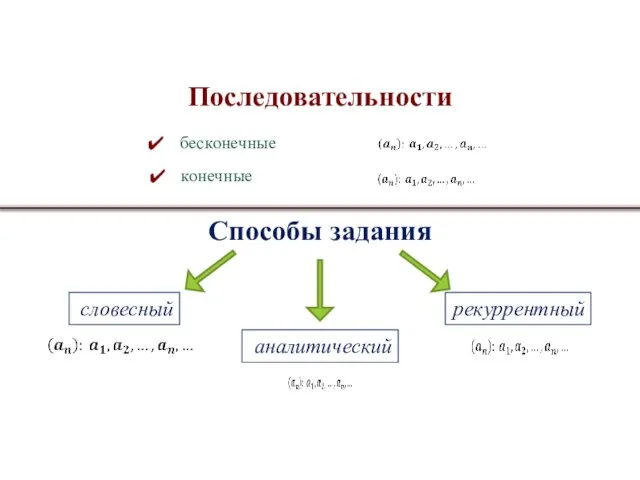
- 2. Способы задания словесный рекуррентный аналитический Последовательности бесконечные конечные
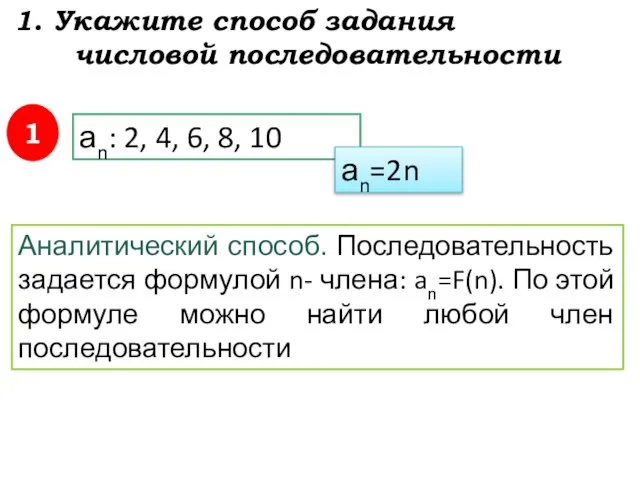
- 3. 1. Укажите способ задания числовой последовательности 1 Аналитический способ. Последовательность задается формулой n- члена: an=F(n). По
- 4. 2 Укажите способ задания числовой последовательности Словесный способ. Представляет собой закономерность или правило расположения членов последовательности,
- 5. 1. Укажите способ задания числовой последовательности 3 Рекуррентный способ. Этот способ задания последовательности состоит в том,
- 6. 1. Устно назовите закономерности задания последовательностей: 1. 2. 3.
- 7. 2. Запишите зависимость между и членами каждой последовательности 2.
- 8. 3. Запишите зависимость между и членами каждой последовательности 2. an+1=an+5 an+1=an+1 an+1=an-10
- 9. Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и
- 10. Выписать пять первых членов арифметической прогрессии:
- 11. Стр.88, №173 (письменно) Записать первый член и разность арифметической прогрессии: Проверка
- 12. Стр.88, №173(письменно) Записать первый член и разность арифметической прогрессии:
- 13. Стр.88, №173 Из данных арифметических прогрессий отметьте те, которые являются возрастающими «+», убывающими «-»? Проверка
- 14. Из данных арифметических прогрессий отметьте те, которые являются возрастающими «+», убывающими ? «+» «+» «+» «-»
- 15. Заполните пропуски: Если разность арифметической прогрессии положительна, то прогрессия является …, а если отрицательной, то …
- 16. Если разность арифметической прогрессии положительна, то прогрессия является возрастающей, а если отрицательной, то убывающей возрастающая возрастающая
- 17. Общий вывод:
- 18. Стр.88, №174(1) Записать первые пять членов арифметической прогрессии: Проверка
- 19. Стр.88, №174(1) Записать первые пять членов арифметической прогрессии:
- 20. Стр.85. Задача 1
- 21. Стр.88. №175(3) Доказать, что последовательность, заданная формулой п-го члена, является арифметической прогрессией Решаем по плану задачи
- 22. Стр.88. №175(3) Доказать, что последовательность, заданная формулой п-го члена, является арифметической прогрессией Решаем по плану задачи
- 23. Стр.88. №175(3) Доказать, что последовательность, заданная формулой п-го члена, является арифметической прогрессией Решаем по плану задачи
- 24. Стр.88. №175(3) Доказать, что последовательность, заданная формулой п-го члена, является арифметической прогрессией Решаем по плану задачи
- 25. Стр.88. №175(3) Доказать, что последовательность, заданная формулой п-го члена, является арифметической прогрессией Решаем по плану задачи
- 26. Стр.88. №175(3) Доказать, что последовательность, заданная формулой п-го члена, является арифметической прогрессией Решаем по плану задачи
- 27. Стр.88. №175(3) Доказать, что последовательность, заданная формулой п-го члена, является арифметической прогрессией Решаем по плану задачи
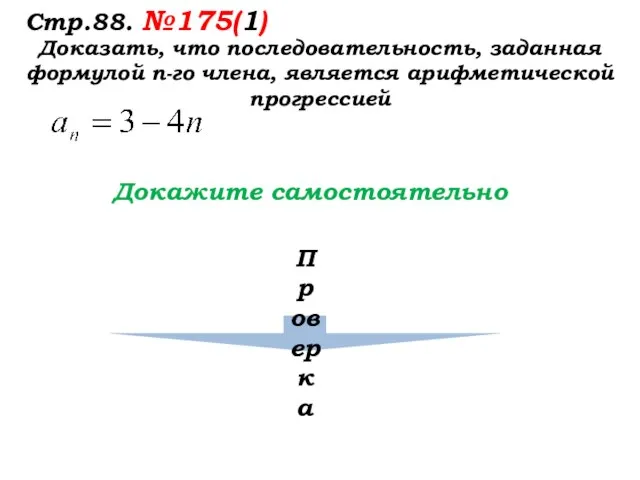
- 28. Стр.88. №175(1) Доказать, что последовательность, заданная формулой п-го члена, является арифметической прогрессией Докажите самостоятельно Проверка
- 29. Стр.88. №175(1) Доказать, что последовательность, заданная формулой п-го члена, является арифметической прогрессией Докажите самостоятельно не зависит
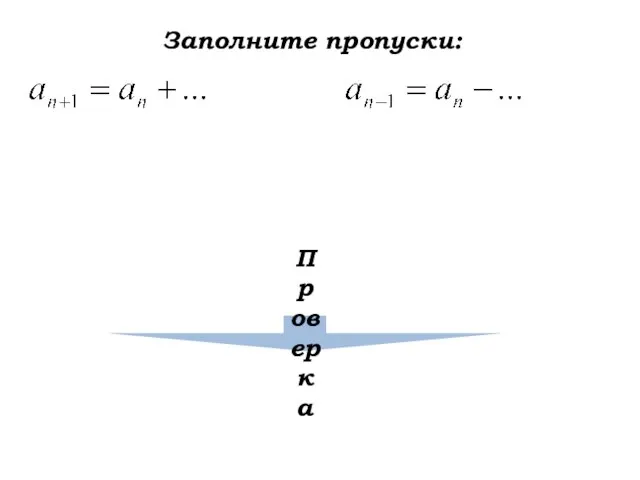
- 30. Заполните пропуски: Проверка
- 31. Заполните пропуски: Проверка
- 32. Заполните пропуски: Проверка
- 33. Заполните пропуски: Стр.85. Основное свойство (характеристическое свойство) арифметической прогрессии
- 34. Найдите члены арифметической прогрессии: Решение
- 35. Найдите члены арифметической прогрессии: Проверка
- 36. Найдите члены арифметической прогрессии:
- 37. Дана арифметическая прогрессия с разностью Заполните пропуски: Проверка
- 38. Дана арифметическая прогрессия с разностью Заполните пропуски: Проверка
- 39. Дана арифметическая прогрессия с разностью Заполните пропуски: Проверка
- 40. Дана арифметическая прогрессия с разностью Заполните пропуски: Проверка
- 41. Дана арифметическая прогрессия с разностью Заполните пропуски:
- 42. Дана арифметическая прогрессия с разностью Заполните пропуски: Проверка
- 43. Дана арифметическая прогрессия с разностью Заполните пропуски:
- 44. Стр.88. №176(1,3) В арифметической прогрессии найти Проверка
- 45. Стр.88. №176(1,3) В арифметической прогрессии найти
- 46. Стр.88. №176(1,3) В арифметической прогрессии найти Проверка
- 48. Скачать презентацию









































 Квадратные неравенства
Квадратные неравенства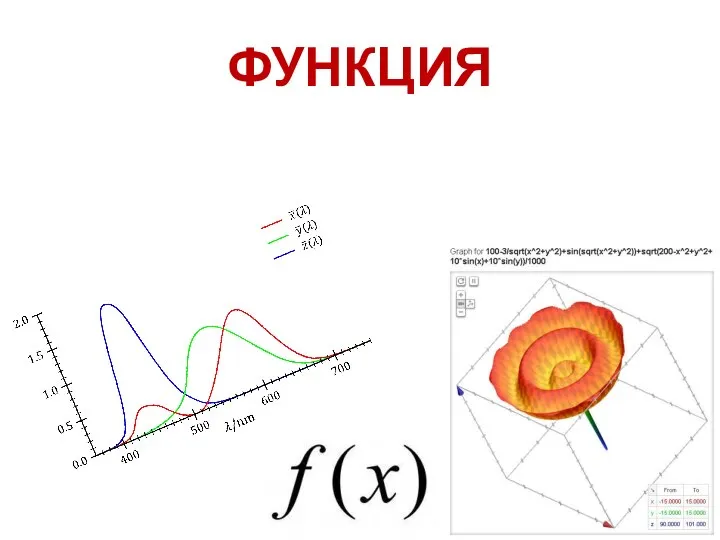 Понятие функции
Понятие функции قدرمطلقی درجه اول
قدرمطلقی درجه اول Приемы решения целых уравнений
Приемы решения целых уравнений Арифметический квадратный корень. Самостоятельная работа
Арифметический квадратный корень. Самостоятельная работа Площадь трапеции
Площадь трапеции Решение задач на движение
Решение задач на движение Вводная лекция. Урок 1
Вводная лекция. Урок 1 Презентация на тему Формирование и развитие УУД на уроках математики
Презентация на тему Формирование и развитие УУД на уроках математики  Уравнение сферы
Уравнение сферы Математика в профессиях
Математика в профессиях Цилиндр. 4 класс
Цилиндр. 4 класс Повторение курса алгебры (7 класс)
Повторение курса алгебры (7 класс) Тангенс суммы и разности аргументов
Тангенс суммы и разности аргументов Однородные тригонометрические уравнения
Однородные тригонометрические уравнения Игра Паркетчик
Игра Паркетчик 3.7. Непрерывность функции
3.7. Непрерывность функции Тригонометрические графики
Тригонометрические графики Решение системы уравнений первой степени с двумя неизвестными
Решение системы уравнений первой степени с двумя неизвестными Математика для перемен
Математика для перемен Умножение десятичной дроби на обыкновенную
Умножение десятичной дроби на обыкновенную Элективный курс по теории вероятностей
Элективный курс по теории вероятностей Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций. Урок 45
Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций. Урок 45 Понятие функции
Понятие функции Неравенства (9 класс)
Неравенства (9 класс) Презентация на тему Квадратичная функция, её свойства и график
Презентация на тему Квадратичная функция, её свойства и график  Теорема Пифагора. 8 класс
Теорема Пифагора. 8 класс Четность, нечетность периодичность функций
Четность, нечетность периодичность функций