Содержание
- 2. Прямоугольник это параллелограмм у которого все углы прямые СВОЙСТВА ПРЯМОУГОЛЬНИКА: 1.Противоположные стороны равны. 2. Диагонали точкой
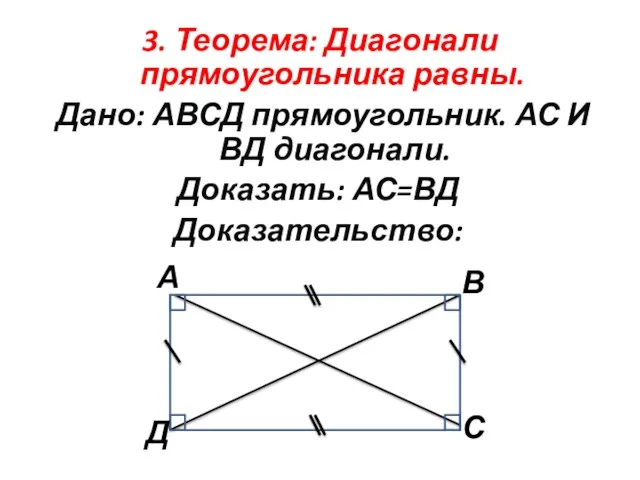
- 3. 3. Теорема: Диагонали прямоугольника равны. Дано: АВСД прямоугольник. АС И ВД диагонали. Доказать: АС=ВД Доказательство:
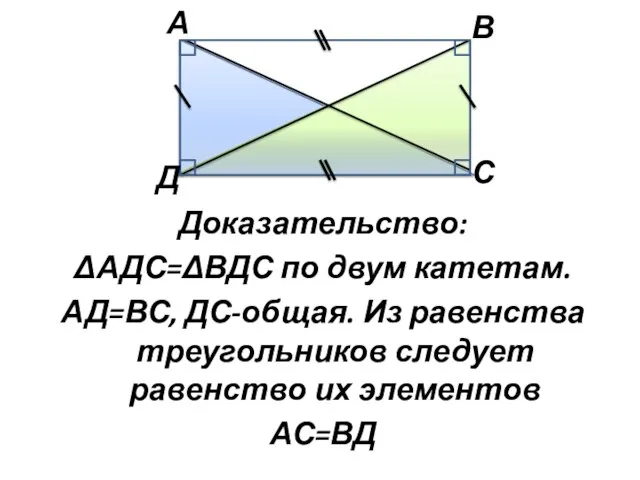
- 4. Доказательство: ΔАДС=ΔВДС по двум катетам. АД=ВС, ДС-общая. Из равенства треугольников следует равенство их элементов АС=ВД
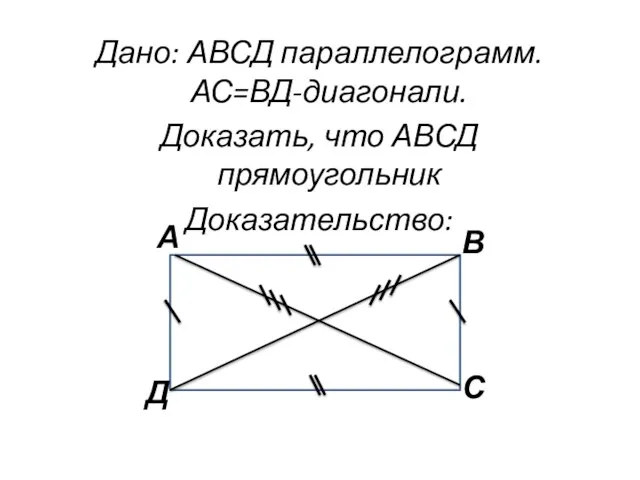
- 5. Теорема (Признак прямоугольника) Если в параллелограмме диагонали равны, то этот параллелограмм прямоугольник.
- 6. Дано: АВСД параллелограмм. АС=ВД-диагонали. Доказать, что АВСД прямоугольник Доказательство:
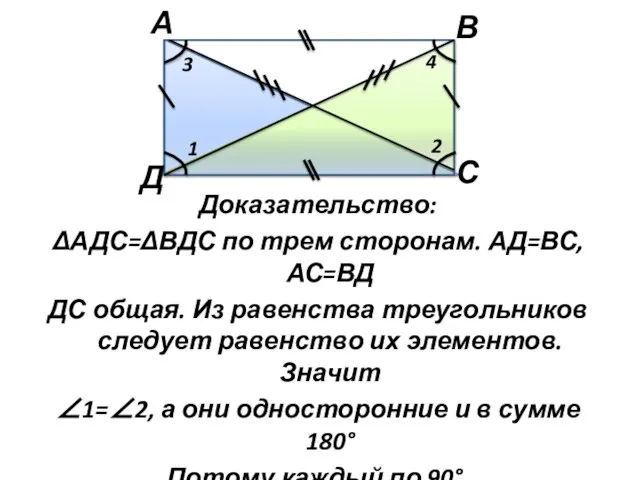
- 7. Доказательство: ΔАДС=ΔВДС по трем сторонам. АД=ВС, АС=ВД ДС общая. Из равенства треугольников следует равенство их элементов.
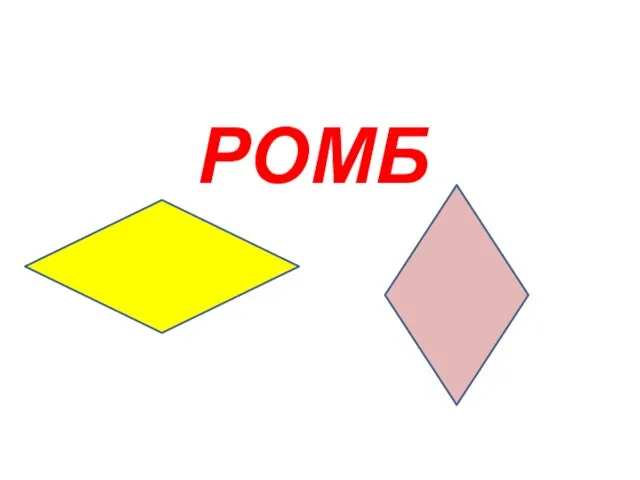
- 8. РОМБ
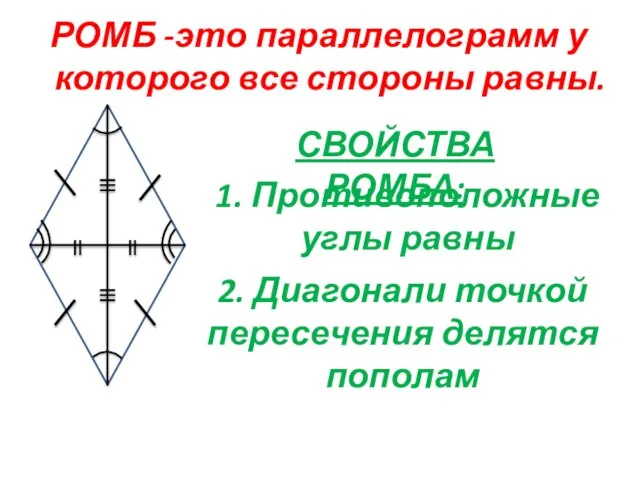
- 9. РОМБ -это параллелограмм у которого все стороны равны. 2. Диагонали точкой пересечения делятся пополам СВОЙСТВА РОМБА:
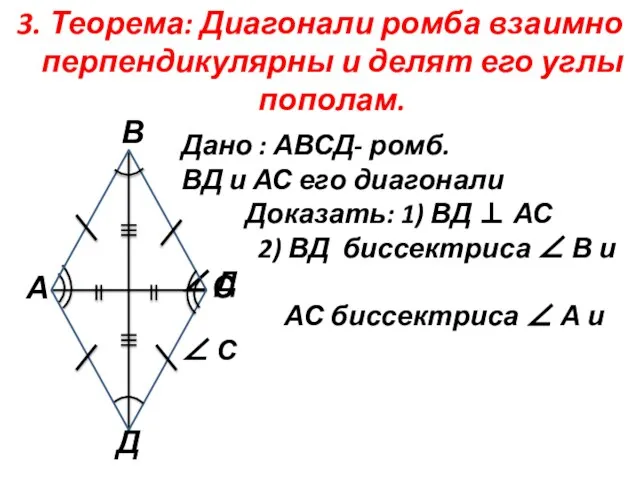
- 10. 3. Теорема: Диагонали ромба взаимно перпендикулярны и делят его углы пополам. Дано : АВСД- ромб. ВД
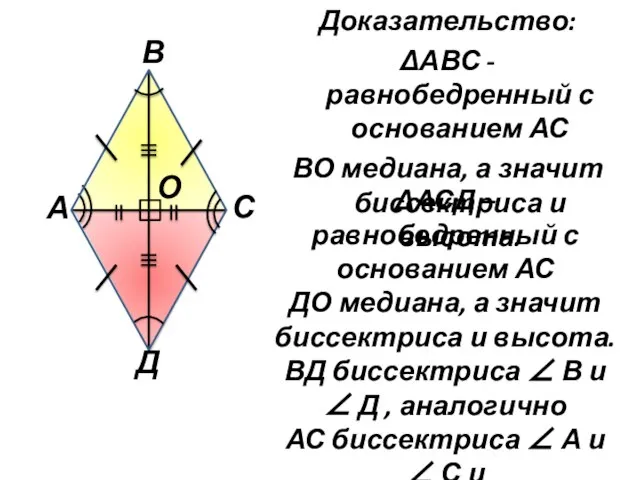
- 11. Доказательство: ΔАВС - равнобедренный с основанием АС ВО медиана, а значит биссектриса и высота. ΔАСД –
- 12. КВАДРАТ
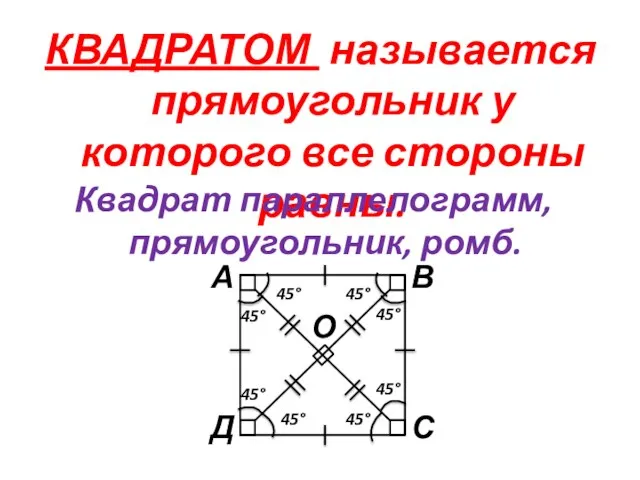
- 13. КВАДРАТОМ называется прямоугольник у которого все стороны равны. Квадрат параллелограмм, прямоугольник, ромб. О
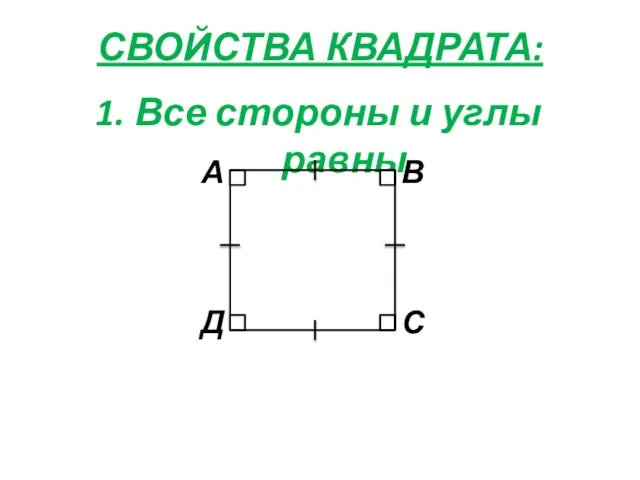
- 14. СВОЙСТВА КВАДРАТА: 1. Все стороны и углы равны
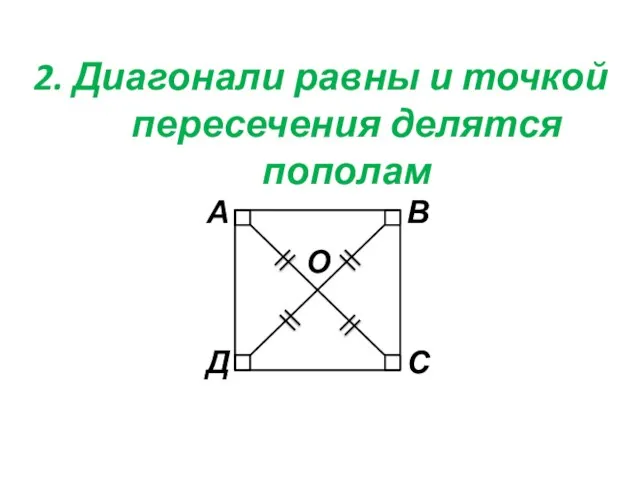
- 15. 2. Диагонали равны и точкой пересечения делятся пополам О
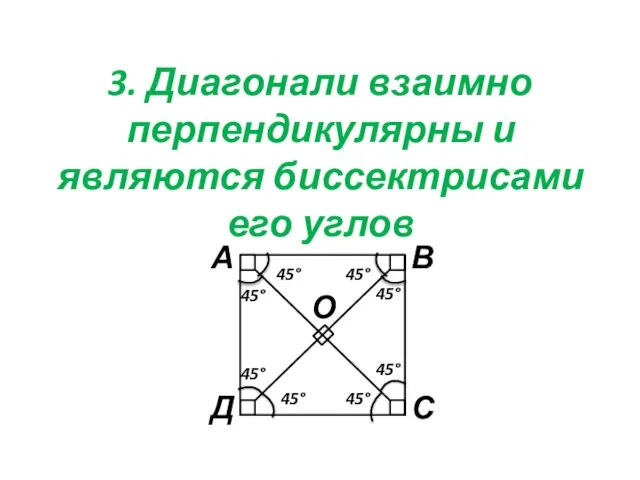
- 16. 3. Диагонали взаимно перпендикулярны и являются биссектрисами его углов О
- 17. ОСЕВАЯ И ЦЕНТРАЛЬНАЯ СИММЕТРИИ.
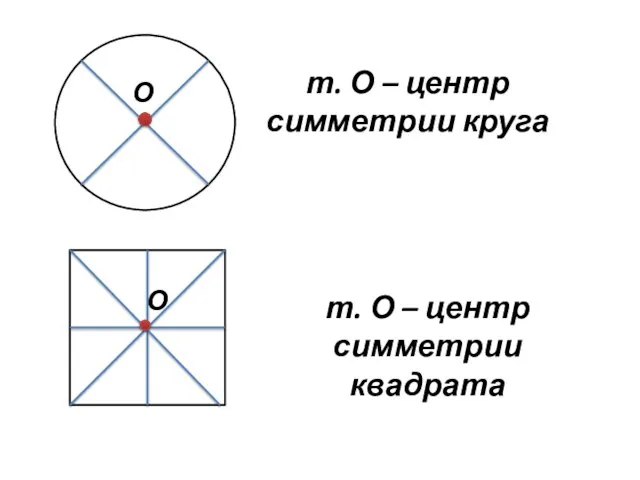
- 18. Центральная симметрия-это симметрия относительно точки.
- 21. т. О – центр симметрии круга т. О – центр симметрии квадрата
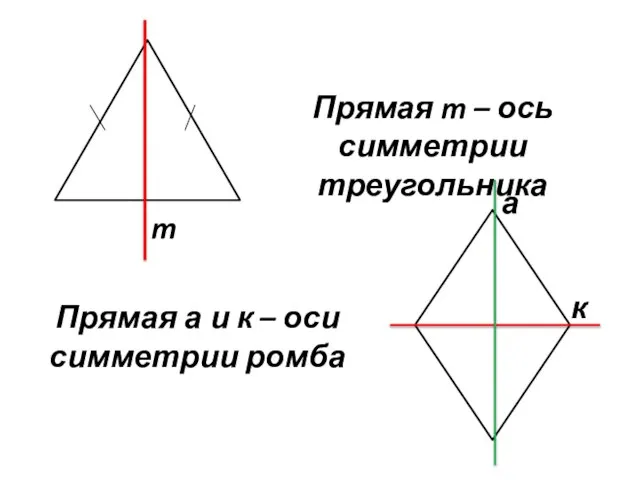
- 25. Осевая симметрия – это симметрия относительно прямой.
- 26. Прямая m – ось симметрии треугольника Прямая а и к – оси симметрии ромба m а
- 33. Скачать презентацию















 Нахождение площади фигур и объемов тел
Нахождение площади фигур и объемов тел Задачи на уменьшение числа на несколько единиц
Задачи на уменьшение числа на несколько единиц Решение уравнений и неравенств с модулем
Решение уравнений и неравенств с модулем Собираемся в путешествие. Решение уравнений. Закрепление пройденного материала
Собираемся в путешествие. Решение уравнений. Закрепление пройденного материала Нахождение корней уравнения с помощью подбора параметра
Нахождение корней уравнения с помощью подбора параметра повторение 7-9
повторение 7-9 Сложение и вычитание трёхзначных чисел. Геометрическое задание
Сложение и вычитание трёхзначных чисел. Геометрическое задание Мир в поверхности цилиндра
Мир в поверхности цилиндра Случайные сигналы и их математические модели
Случайные сигналы и их математические модели Состав числа 5
Состав числа 5 Натуральные числа. Викторина
Натуральные числа. Викторина Признаки равенства треугольников
Признаки равенства треугольников Понятие о комплексных числах. Рациональные функции одной переменной
Понятие о комплексных числах. Рациональные функции одной переменной Четырехугольники
Четырехугольники Комплексные числа
Комплексные числа Дроби
Дроби Тренажер. Единицы площади
Тренажер. Единицы площади Применение инверсии при построении графиков
Применение инверсии при построении графиков Лабораторно-практическая работа в парах
Лабораторно-практическая работа в парах Математика, Устный счёт
Математика, Устный счёт Вычисление площадей фигур с помощью интеграла
Вычисление площадей фигур с помощью интеграла Знаки тригонометрических функций. Формулы сложения
Знаки тригонометрических функций. Формулы сложения Предел последовательности. Бесконечно убывающая геометрическая прогрессия
Предел последовательности. Бесконечно убывающая геометрическая прогрессия Танграм (древняя китайская головоломка)
Танграм (древняя китайская головоломка) Урок по теме: Умножение десятичной дроби на 10, 100, 1000… по учебнику "Математика", Зубарева И.И., Мордкович А.Г.: Учебник для 5 класса общеобразовательных учреждений
Урок по теме: Умножение десятичной дроби на 10, 100, 1000… по учебнику "Математика", Зубарева И.И., Мордкович А.Г.: Учебник для 5 класса общеобразовательных учреждений Векторы в пространстве
Векторы в пространстве Тригонометрические функции. Их свойства и график (1)
Тригонометрические функции. Их свойства и график (1) Математическая логика. Логические выражения
Математическая логика. Логические выражения