Содержание
- 2. Построение графиков функций по известным графикам данных функций. Пусть уже построен график функции y=f(x). Используя этот
- 3. Содержание: график y=f(x-a) график y=f(kx), где k>0 график y=f(|x|) график y=f(x)+b график y=|f(x)| пример
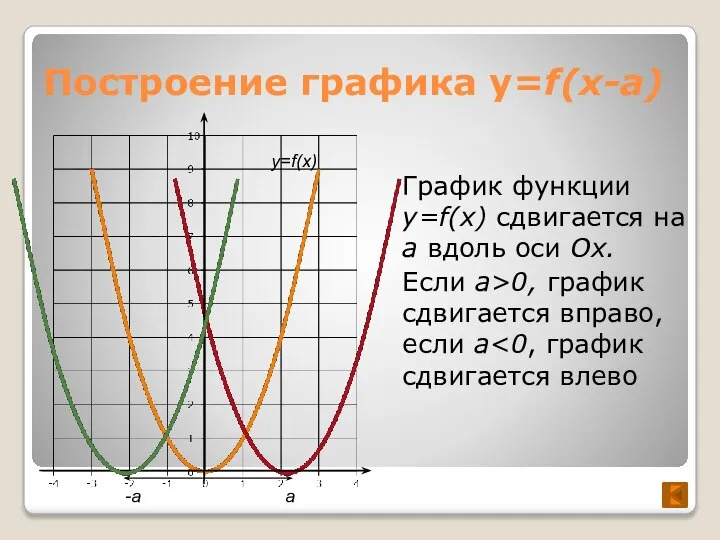
- 4. Построение графика y=f(x-a) График функции y=f(x) сдвигается на a вдоль оси Ox. Если а>0, график сдвигается
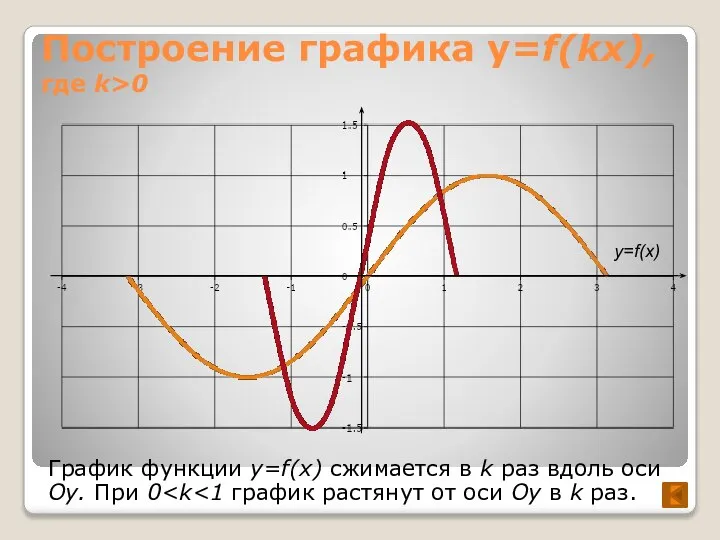
- 5. Построение графика y=f(kx), где k>0 График функции y=f(x) сжимается в k раз вдоль оси Oy. При
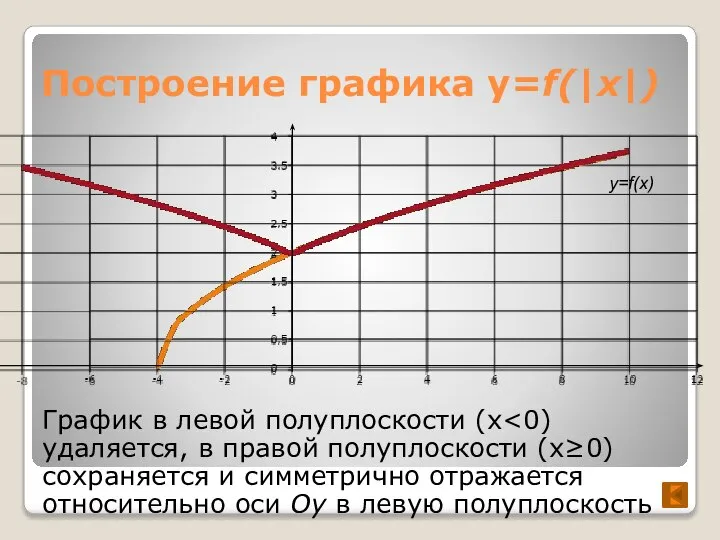
- 6. Построение графика y=f(|x|) График в левой полуплоскости (x y=f(x)
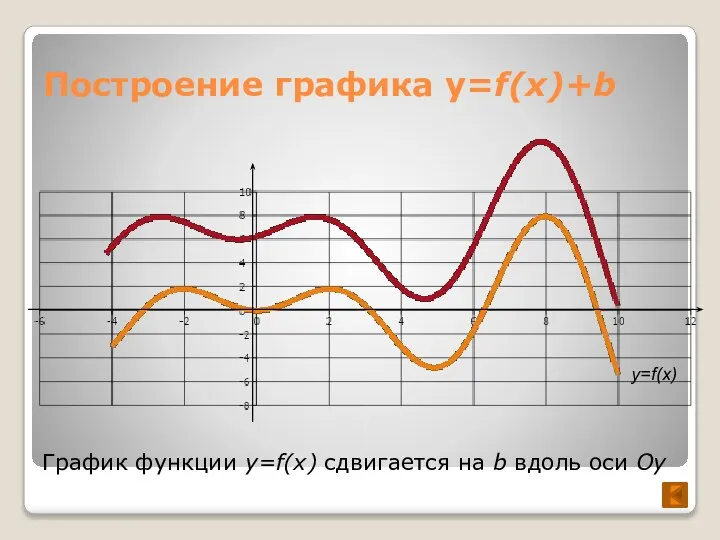
- 7. Построение графика y=f(x)+b График функции y=f(x) сдвигается на b вдоль оси Oy y=f(x)
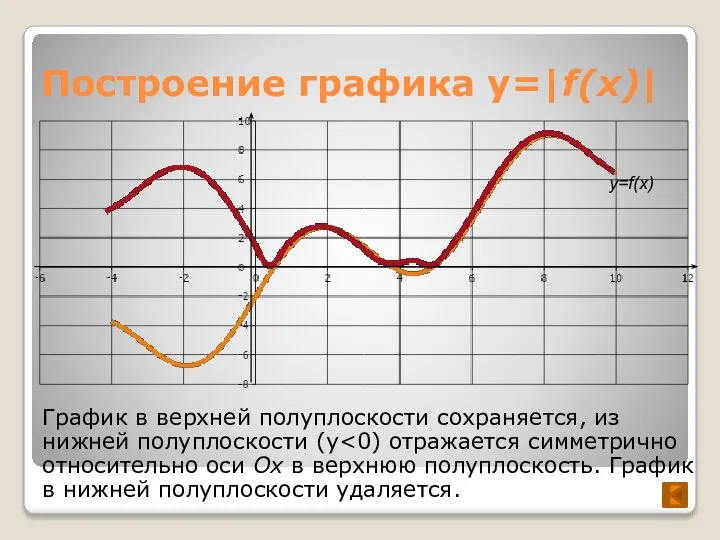
- 8. Построение графика y=|f(x)| График в верхней полуплоскости сохраняется, из нижней полуплоскости (y y=f(x)
- 10. Скачать презентацию


 Свойства функций
Свойства функций Классическое определение вероятности
Классическое определение вероятности Темір жолдың жылжымалы құрамын пайдалану, жөндеу және техникалық қызмет көрсету (түрлері бойынша)
Темір жолдың жылжымалы құрамын пайдалану, жөндеу және техникалық қызмет көрсету (түрлері бойынша) Множества и отображения
Множества и отображения Цилиндр
Цилиндр Математический биатлон
Математический биатлон pril
pril Презентация на тему Подобие треугольников
Презентация на тему Подобие треугольников  Логарифмы
Логарифмы Лекция 5_1_СЛАУ_Итерац методы
Лекция 5_1_СЛАУ_Итерац методы Преобразование логарифмических выражений
Преобразование логарифмических выражений Упрощение выражений. Решение уравнений
Упрощение выражений. Решение уравнений Постер-фракталы для интерьера
Постер-фракталы для интерьера Задание на треугольники
Задание на треугольники Проверочная работа
Проверочная работа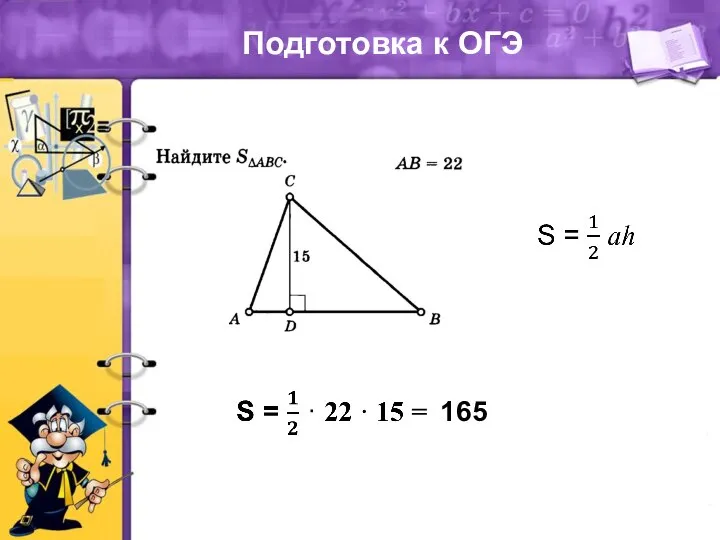 Теорема площади треугольника. Подготовка к ОГЭ
Теорема площади треугольника. Подготовка к ОГЭ Диаграммы Ламерея. Качественный анализ дискретных ДС
Диаграммы Ламерея. Качественный анализ дискретных ДС многогранники
многогранники Блиц-турнир по математике
Блиц-турнир по математике Письменное умножение на трёхзначное число
Письменное умножение на трёхзначное число Презентация на тему Подготовка к ЕГЭ по математике
Презентация на тему Подготовка к ЕГЭ по математике  Численные методы решения дифференциальных уравнений
Численные методы решения дифференциальных уравнений Презентация на тему Центральная и осевая симметрии в природе
Презентация на тему Центральная и осевая симметрии в природе  На что похож наш ноль?
На что похож наш ноль? Организация исследовательской деятельности учащихся по математике
Организация исследовательской деятельности учащихся по математике Презентация на тему Формулы квадрата суммы и квадрата разности двух выражений
Презентация на тему Формулы квадрата суммы и квадрата разности двух выражений  Что такое медиана?
Что такое медиана? Элементы теории фредгольмовых отображений
Элементы теории фредгольмовых отображений