Содержание
- 2. Числовые Функции и графики
- 3. немного из истории А знаете ли вы...
- 4. Функция – это одно из основных общенаучных и математических понятий, выражающее зависимость между переменными величинами. Слово
- 5. Один из самых замечательных математиков Леонард Эйлер (1707 – 1783), вводя понятие функции, говорил, что «когда
- 6. «Когда математика стала изучать переменные величины и функции, как только она научилась описывать процессы, движение, так
- 7. Функции вокруг нас
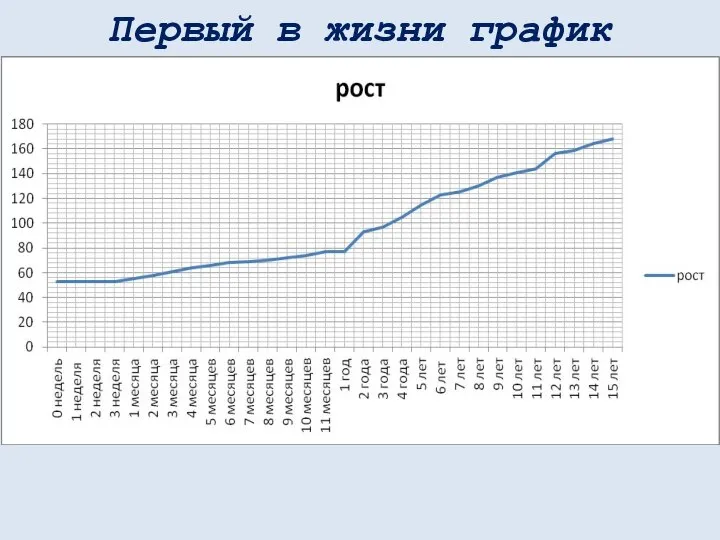
- 8. Первый в жизни график
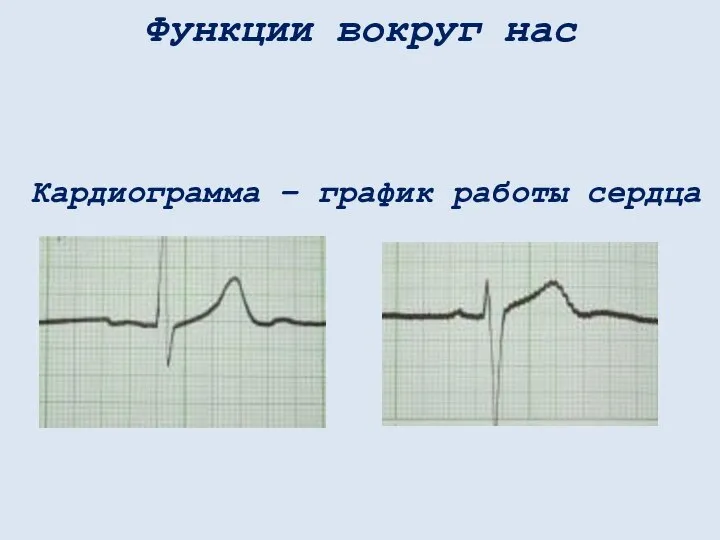
- 9. Кардиограмма – график работы сердца Функции вокруг нас
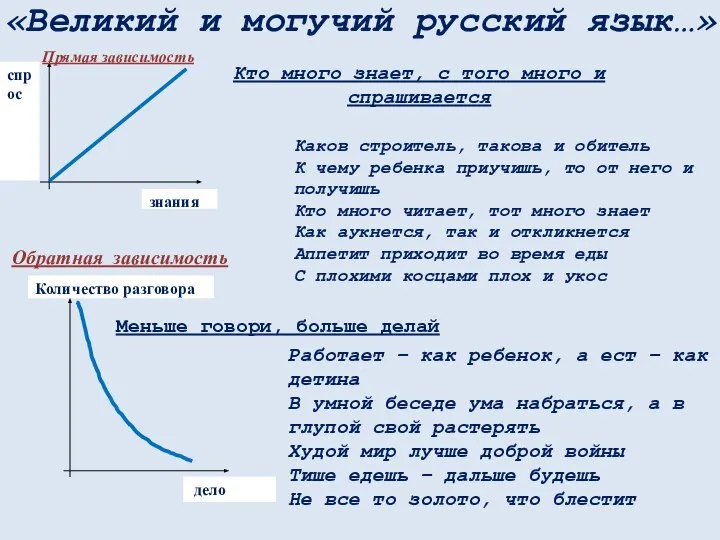
- 10. «Великий и могучий русский язык…» И сокол выше солнца не летает Бездонную бочку водой не наполнишь
- 11. «Великий и могучий русский язык…» Кто много знает, с того много и спрашивается Каков строитель, такова
- 12. Алгебраическая разминка
- 13. Сегодня здесь затеи и задачи, Смех и шутки не для нас! Пожелаем всем удачи – За
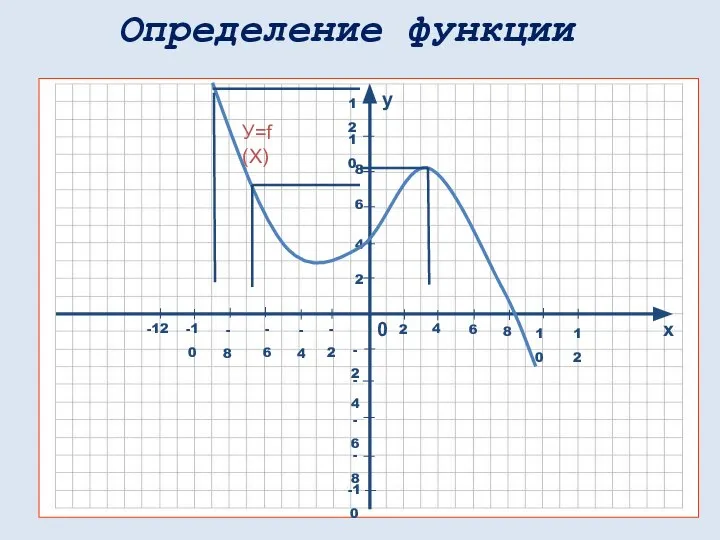
- 14. У=f (X) Определение функции
- 15. МНОЖЕСТВО Х: ВСЕ ЖИЛЬЦЫ МНОЖЕСТВО Y: НОМЕРА КВАРТИР Правило соответствия (зависимости) между множествами : «Каждому жильцу
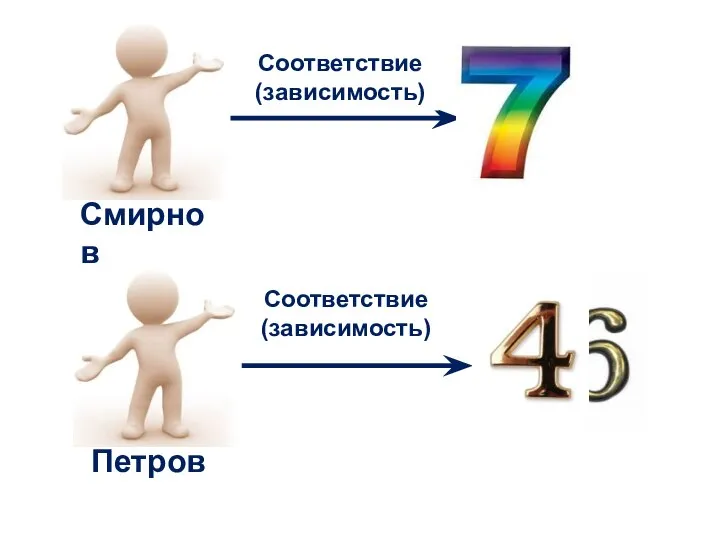
- 16. Смирнов Петров Правило соответствия (зависимости) между множествами : «Каждому жильцу дома будет соответствовать номер его квартиры».
- 17. Петров Смирнов Соответствие (зависимость) Соответствие (зависимость)
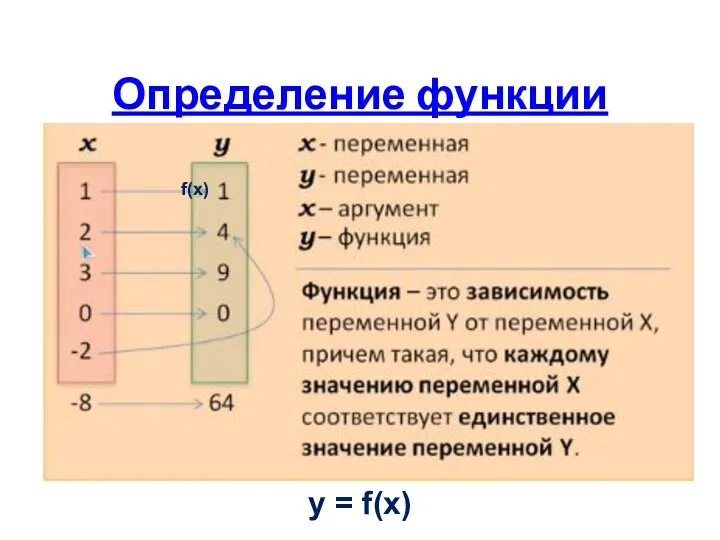
- 18. Определение функции f(x) y = f(x)
- 19. Что такое функция? Функциональная зависимость, или функция, - это такая зависимость между двумя переменными, при которой
- 20. Существует несколько способов задания функции: 1.С помощью таблицы. 2.Графический. 3.С помощью формулы. Графиком функции называется множество
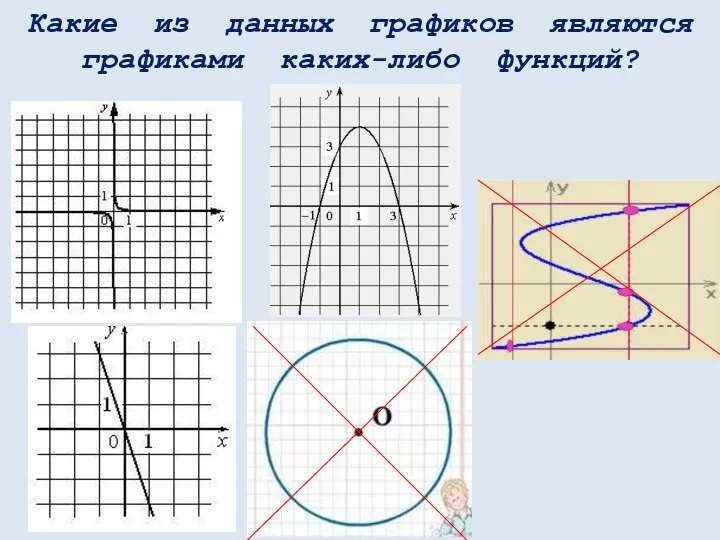
- 21. Какие из данных графиков являются графиками каких-либо функций?
- 22. Область определения функции Областью определения функции называют множество всех значений, которые может принимать ее аргумент (х)
- 23. Множество значений функции Множеством значений функции называют множество всех значений которые может принимать переменная у Е(у)
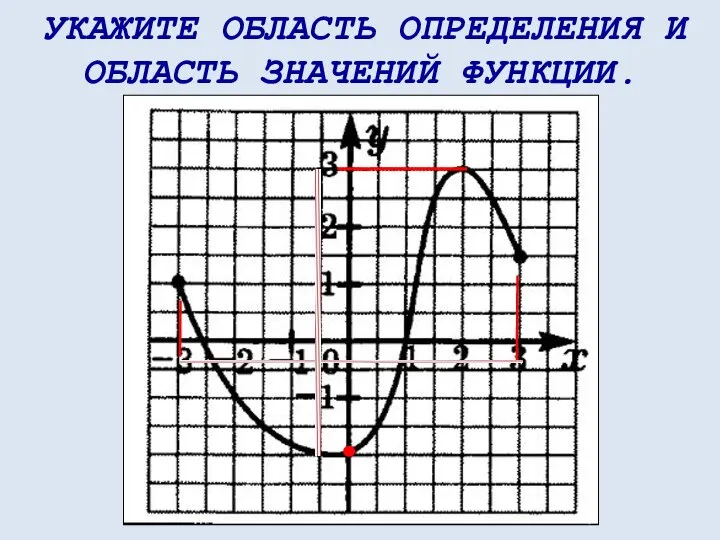
- 24. УКАЖИТЕ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ.
- 25. Функция – зависимость одной переменной от другой, причем для любых значений х соответствует единственное значение функции
- 26. Найдите область определения и значений функции 5 ( -1;5] -3 4 [ -3;4) а) б) в)
- 27. Промежутки, в которых функция сохраняет знак, называют промежутками знакопостоянства У>0 при X∈ (-3; 7); У У=0
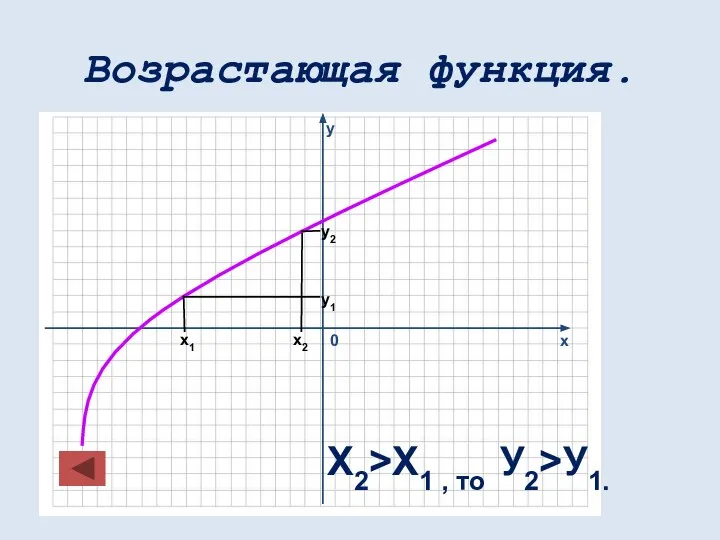
- 28. Возрастающая функция. х1 х2 у1 у2 Х2>Х1 , то У2>У1.
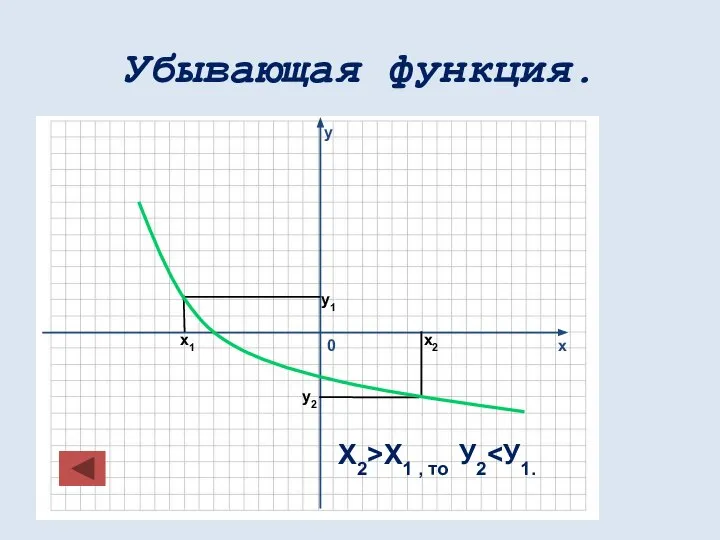
- 29. Убывающая функция. х1 х2 у1 у2 Х2>Х1 , то У2
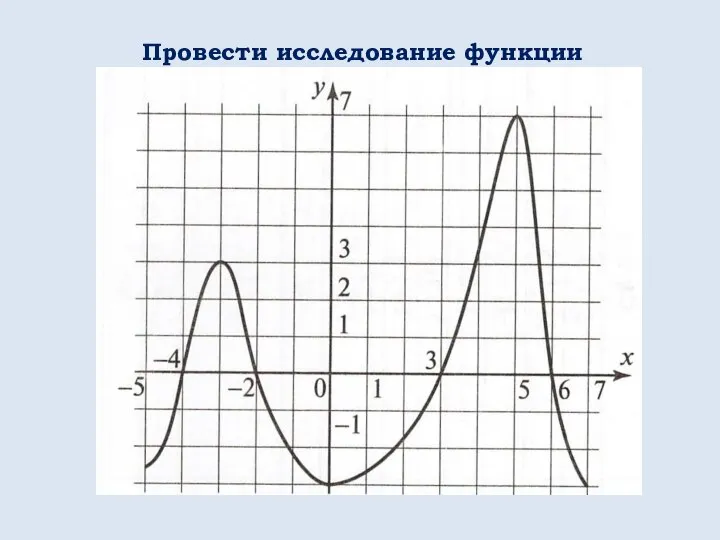
- 30. Провести исследование функции
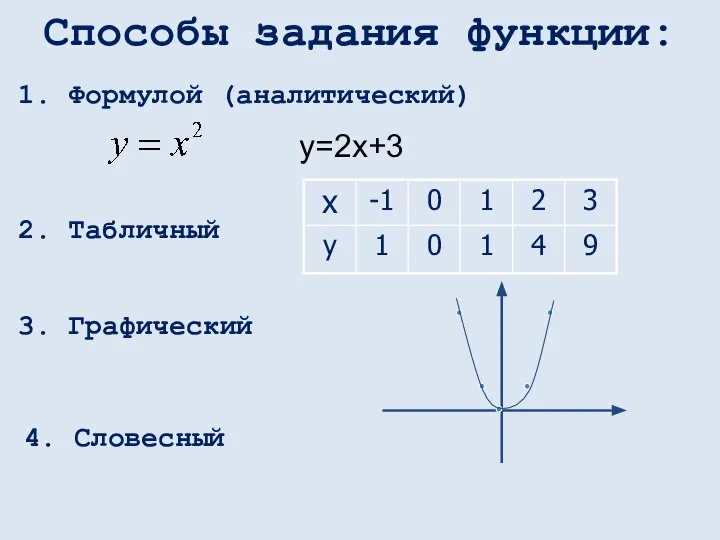
- 31. Способы задания функции: 4. Словесный 2. Табличный 3. Графический 1. Формулой (аналитический) у=2х+3
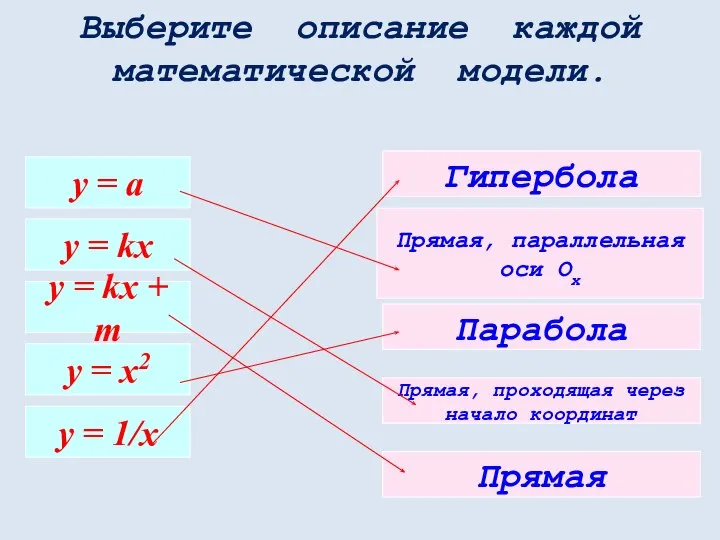
- 32. Виды функций Линейная Прямая пропорциональность Обратная пропорциональность Квадратичная Кубическая Квадратный корень Модуль Преобразование графиков
- 33. Линейные функции. y = ах + b
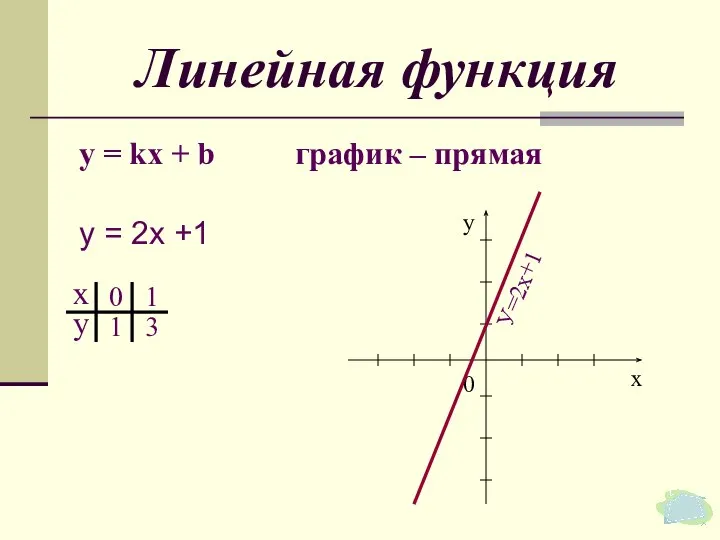
- 34. Линейная функция у = kх + b график – прямая 0 У=2х+1 у = 2х +1
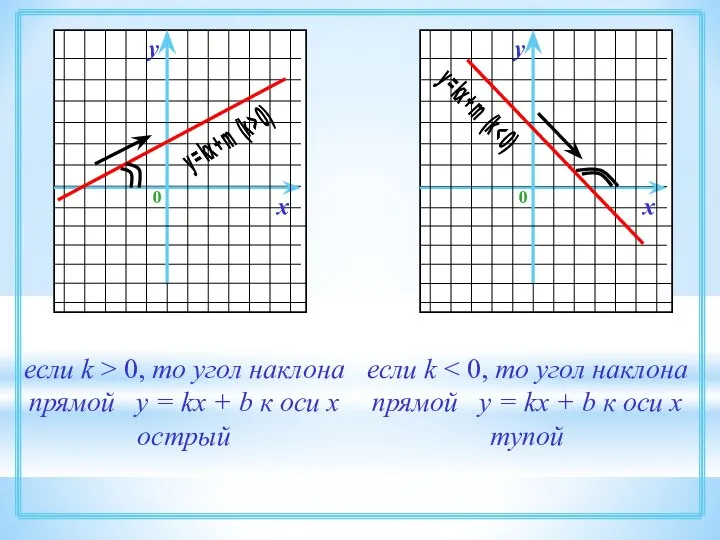
- 35. если k > 0, то угол наклона прямой у = kx + b к оси x
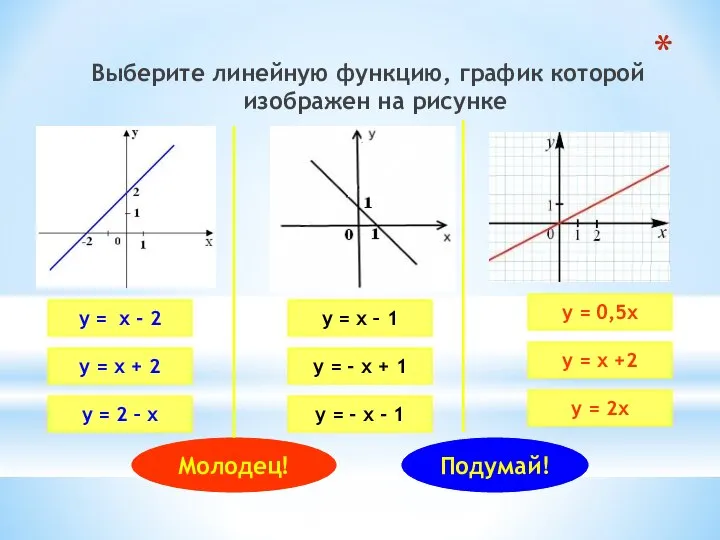
- 36. Выберите линейную функцию, график которой изображен на рисунке у = х - 2 у = х
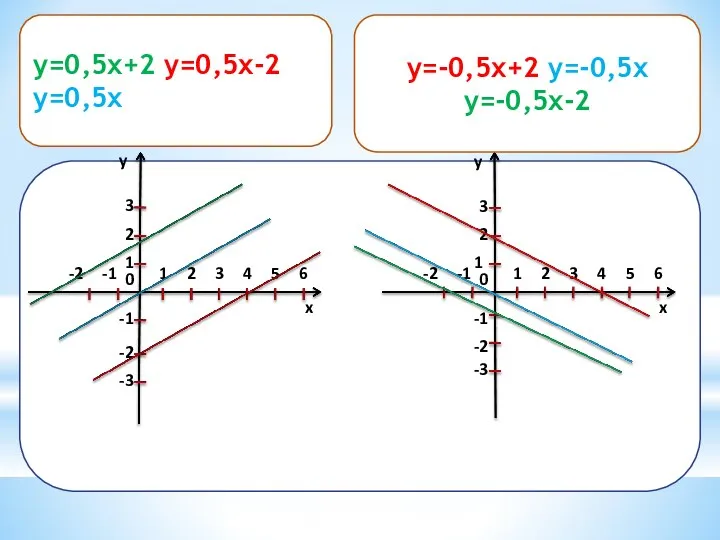
- 37. y=-0,5x+2, y=-0,5x, y=-0,5x-2 x y 1 2 0 1 2 3 -1 -2 -1 -2 3
- 38. Еще раз повторим: *Функция вида у = kx + b называется линейной. *Графиком функции вида у
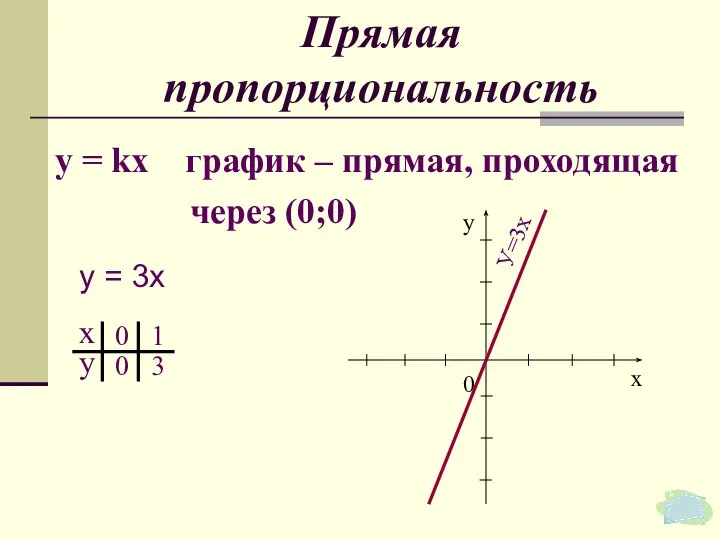
- 39. Функции прямой пропорциональности. у = kx
- 40. Прямая пропорциональность у = kх график – прямая, проходящая через (0;0) У=3х у = 3х
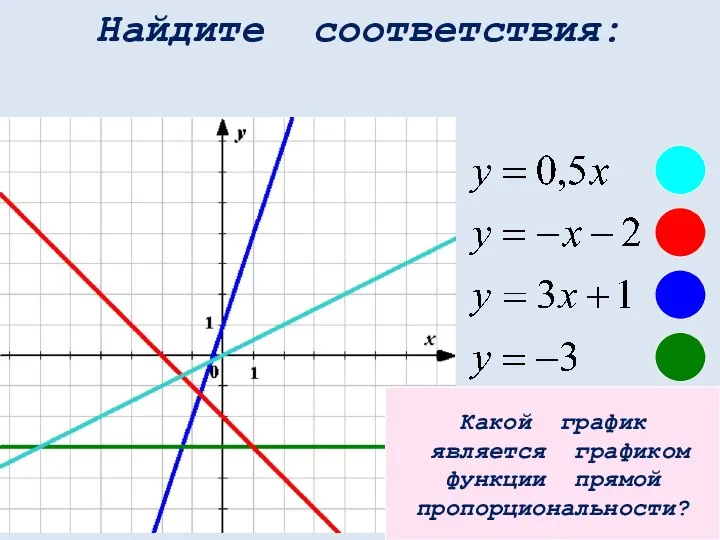
- 41. Найдите соответствия: Какой график является графиком функции прямой пропорциональности?
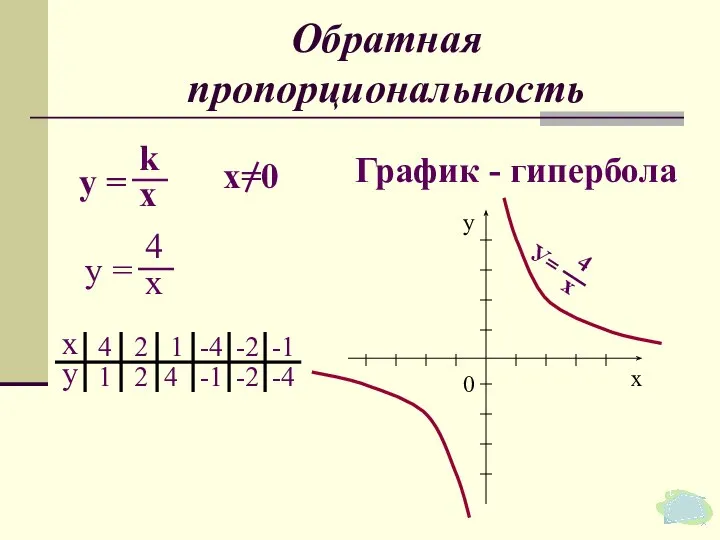
- 42. Функции обратной пропорциональности у = k/x И все!
- 43. Обратная пропорциональность
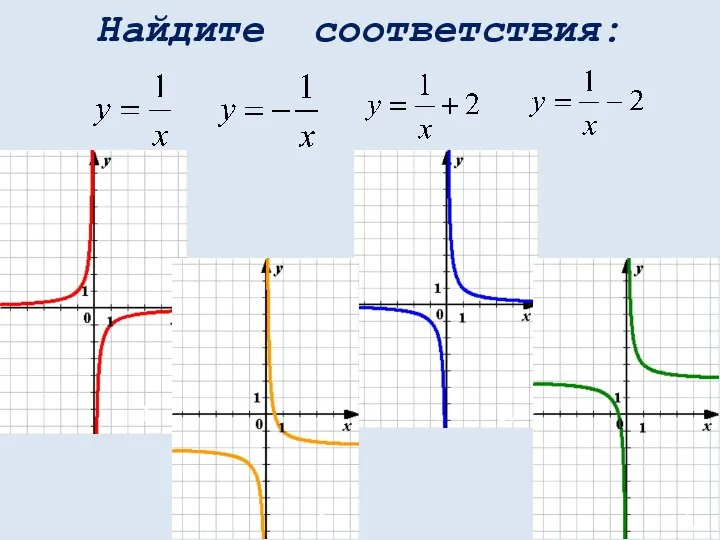
- 44. Найдите соответствия: 1. 3. 2. 4.
- 45. у = а y = kx y = kx + m y = x2 y =
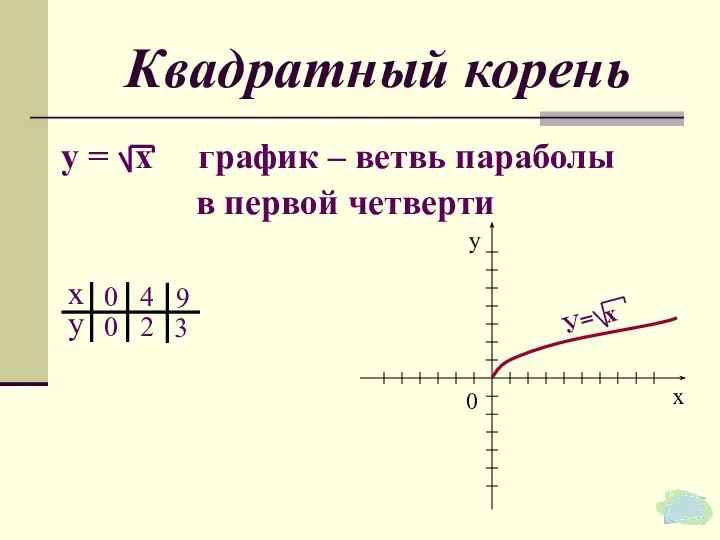
- 46. Квадратный корень у = х график – ветвь параболы в первой четверти
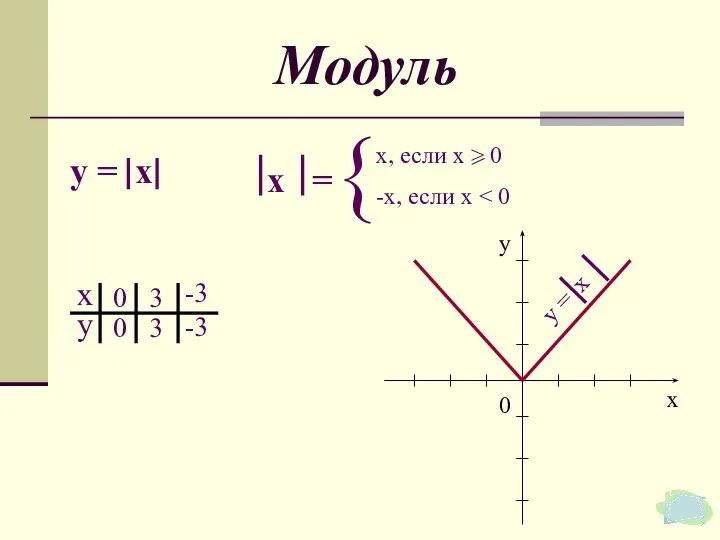
- 47. Модуль
- 48. Ответ:
- 49. Решите самостоятельно: Ответ:
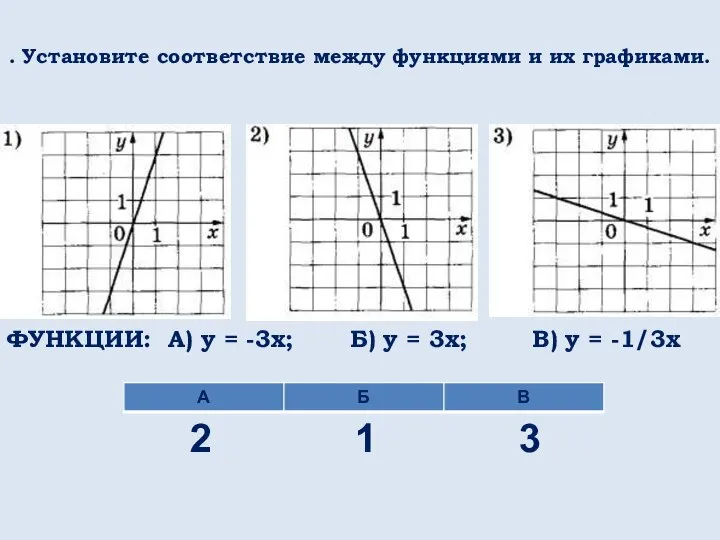
- 50. . Установите соответствие между функциями и их графиками. ФУНКЦИИ: А) y = -3x; Б) y =
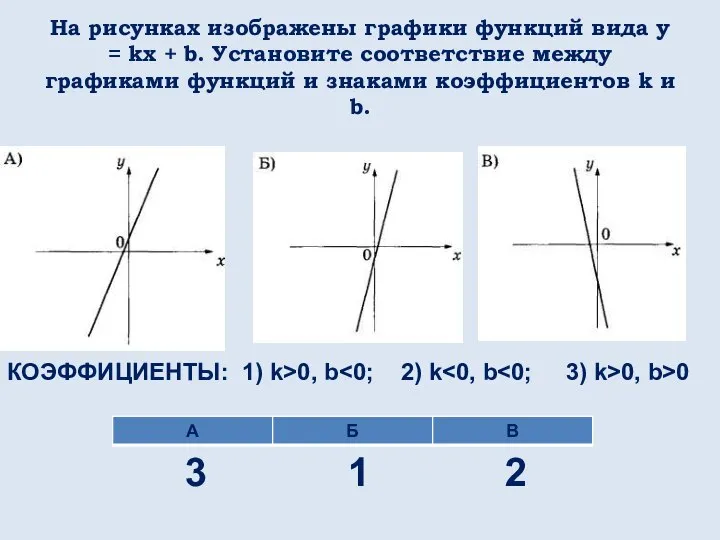
- 51. На рисунках изображены графики функций вида y = kx + b. Установите соответствие между графиками функций
- 53. Скачать презентацию















![Найдите область определения и значений функции 5 ( -1;5] -3 4 [](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/932489/slide-25.jpg)








 Правильный восьмиугольник
Правильный восьмиугольник Свойства корня п- ой степени
Свойства корня п- ой степени Сложение +5
Сложение +5 Задачи на готовых чертежах. Подобные треугольники
Задачи на готовых чертежах. Подобные треугольники Логические элементы
Логические элементы Тема урока: Десятичная система счисления Цели: Познакомиться с системами счисления. Сформировать умение работать с римскими чис
Тема урока: Десятичная система счисления Цели: Познакомиться с системами счисления. Сформировать умение работать с римскими чис Математический КВН. 6 класс
Математический КВН. 6 класс Натуральные числа и дроби. Урок 1
Натуральные числа и дроби. Урок 1 Проецирование правильной шестиугольной призмы
Проецирование правильной шестиугольной призмы Длиннее, короче (1 класс)
Длиннее, короче (1 класс) Математические шифровки
Математические шифровки Понятие функции
Понятие функции Теорема Пифагора. 8 класс
Теорема Пифагора. 8 класс Соседи числа
Соседи числа Представление о ломаной линии и многоугольнике
Представление о ломаной линии и многоугольнике Спин и расширенное супервремя. Суперсимметрия и суперпространство
Спин и расширенное супервремя. Суперсимметрия и суперпространство Блез Паскаль
Блез Паскаль Многогранники
Многогранники Дифференциальное исчисление в нормированных пространствах (задачи)
Дифференциальное исчисление в нормированных пространствах (задачи) Счет и вычисления основа порядка в голове. (Песталоцци)
Счет и вычисления основа порядка в голове. (Песталоцци) Закрепление сложения однозначных чисел с переходом через десяток
Закрепление сложения однозначных чисел с переходом через десяток Возрастание и убывание функции. Экстремумы (10 класс)
Возрастание и убывание функции. Экстремумы (10 класс) Школа олимпийского резерва. (задача)
Школа олимпийского резерва. (задача) Мультиколлинеарность – это взаимное влияние факторов друг на друга
Мультиколлинеарность – это взаимное влияние факторов друг на друга Математика и живопись
Математика и живопись Фигуры на клетчатой бумаге
Фигуры на клетчатой бумаге Lek-AFK-Differentsialnye_uravnenia
Lek-AFK-Differentsialnye_uravnenia Урок математики. Таблица умножения на 7
Урок математики. Таблица умножения на 7