Содержание
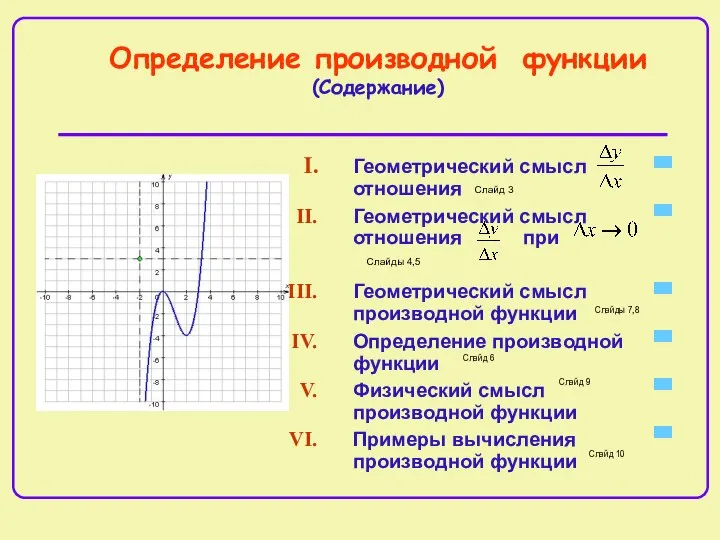
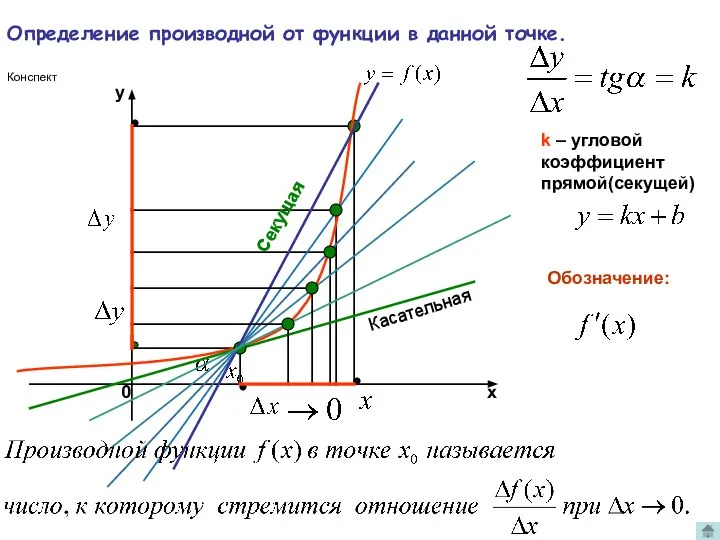
- 2. Определение производной функции (Содержание) Геометрический смысл отношения Геометрический смысл отношения при Геометрический смысл производной функции Определение
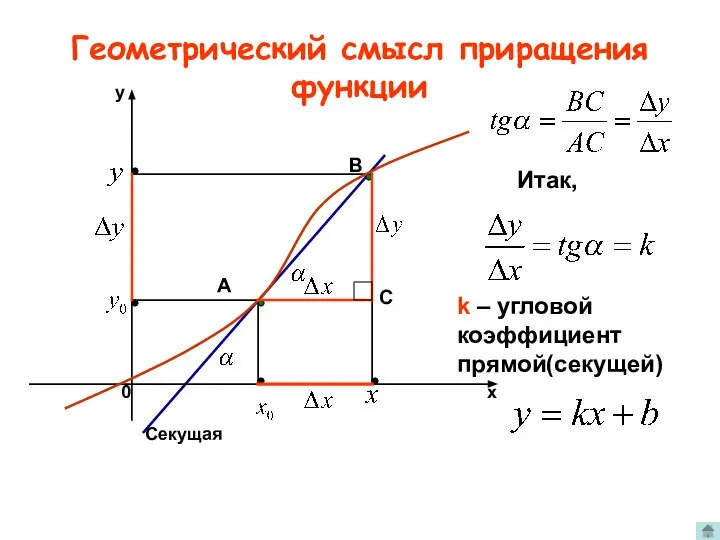
- 3. Геометрический смысл приращения функции A B Секущая С Итак, k – угловой коэффициент прямой(секущей)
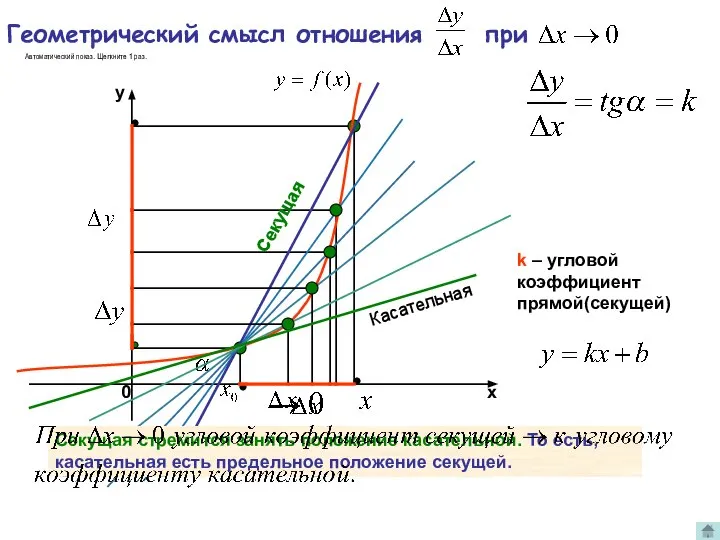
- 4. Геометрический смысл отношения при k – угловой коэффициент прямой(секущей) Секущая стремится занять положение касательной. То есть,
- 5. k – угловой коэффициент прямой(секущей) Секущая стремится занять положение касательной. То есть, касательная есть предельное положение
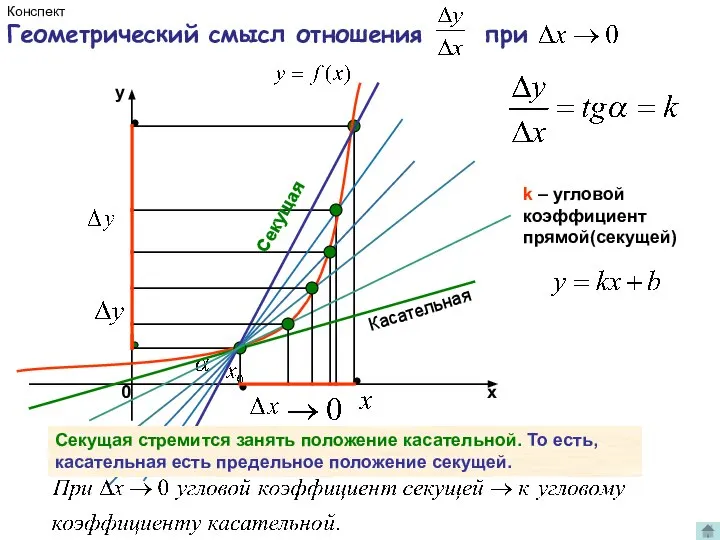
- 6. Определение производной от функции в данной точке. k – угловой коэффициент прямой(секущей) Касательная Секущая Конспект
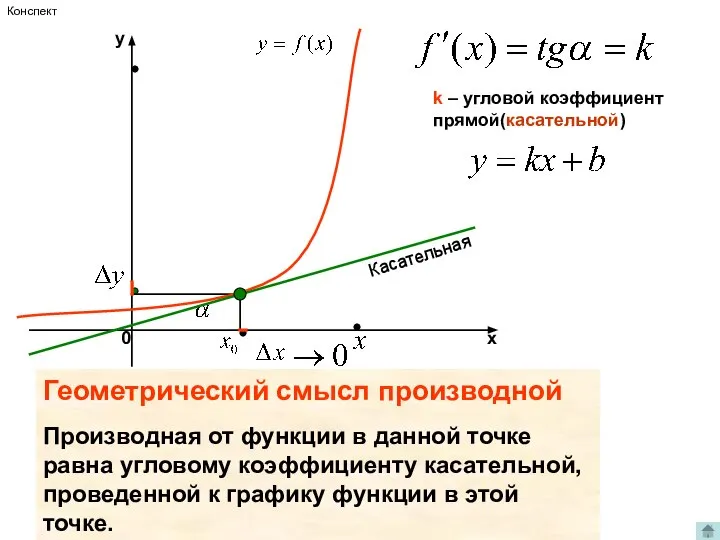
- 7. k – угловой коэффициент прямой(касательной) Касательная Геометрический смысл производной Производная от функции в данной точке равна
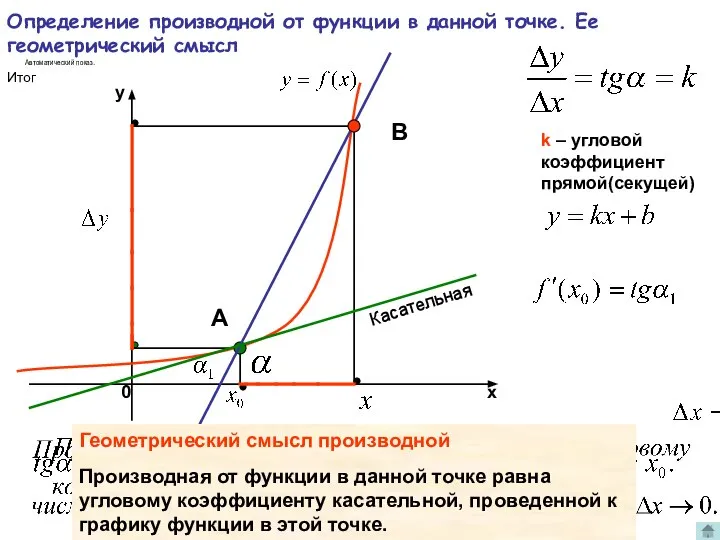
- 8. Определение производной от функции в данной точке. Ее геометрический смысл k – угловой коэффициент прямой(секущей) А
- 9. Физический смысл производной функции в данной точке .
- 11. Скачать презентацию

 Урок по геометрии
Урок по геометрии Взаимно-обратные операции
Взаимно-обратные операции Нулевой угловой коэффицент
Нулевой угловой коэффицент Комплексные числа
Комплексные числа Применение распределительного свойства умножения
Применение распределительного свойства умножения Диаграммы
Диаграммы Презентация на тему Решение задач В ЕГЭ по теории вероятности
Презентация на тему Решение задач В ЕГЭ по теории вероятности  Точка перегиба
Точка перегиба Մաթեմատիկական_ինդուկցիայի_մեթոդը
Մաթեմատիկական_ինդուկցիայի_մեթոդը Основы теории вероятностей. Лекция 113
Основы теории вероятностей. Лекция 113 Нелинейные уравнения с двумя неизвестными
Нелинейные уравнения с двумя неизвестными Плоскость и прямая в пространстве
Плоскость и прямая в пространстве Тестирование генераторов случайных чисел
Тестирование генераторов случайных чисел Sie hat Geburtstag am fünften August. Er kommt am einunddreißigsten Juli
Sie hat Geburtstag am fünften August. Er kommt am einunddreißigsten Juli Эвристические приемы. Алгебра 8 класс
Эвристические приемы. Алгебра 8 класс Математическая игра Петергофская мозаика 5 класс
Математическая игра Петергофская мозаика 5 класс Почти все об углах
Почти все об углах Рисование старинного терема из геометрических форм
Рисование старинного терема из геометрических форм Математический маятник
Математический маятник Площадь треугольника
Площадь треугольника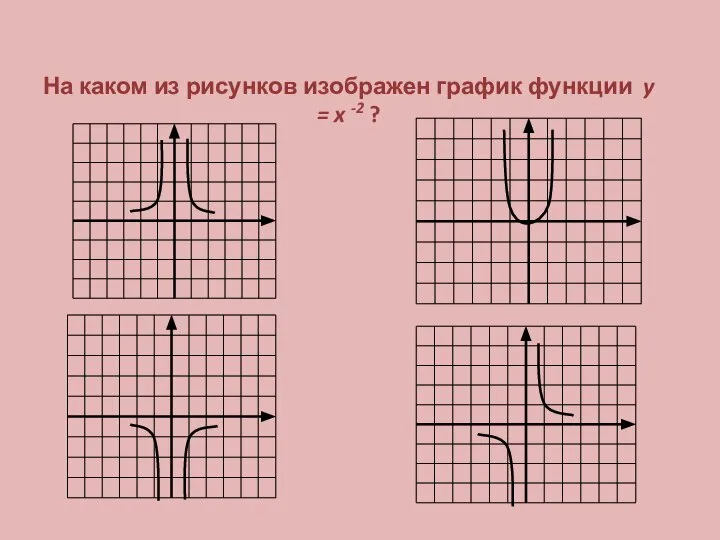 Степенная функция
Степенная функция Подмножество. Операции над множествами. Самостоятельная работа
Подмножество. Операции над множествами. Самостоятельная работа Числовая окружность
Числовая окружность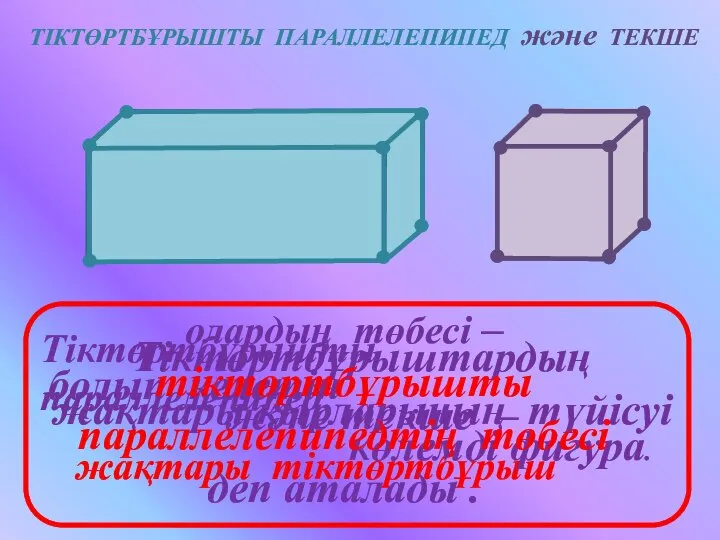 Тіктөртбұрышты параллелепипед және текше
Тіктөртбұрышты параллелепипед және текше Свойства логарифмов
Свойства логарифмов Решение задач (2 класс)
Решение задач (2 класс) Презентация на тему Веселая математика 1 класс
Презентация на тему Веселая математика 1 класс  Показательные неравенства
Показательные неравенства