Содержание
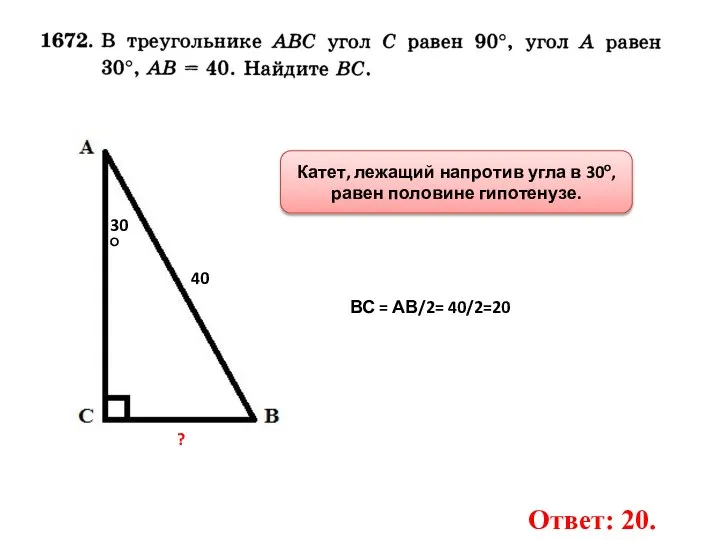
- 2. 30О 40 ? Катет, лежащий напротив угла в 30о, равен половине гипотенузе. ВС = АВ/2= 40/2=20
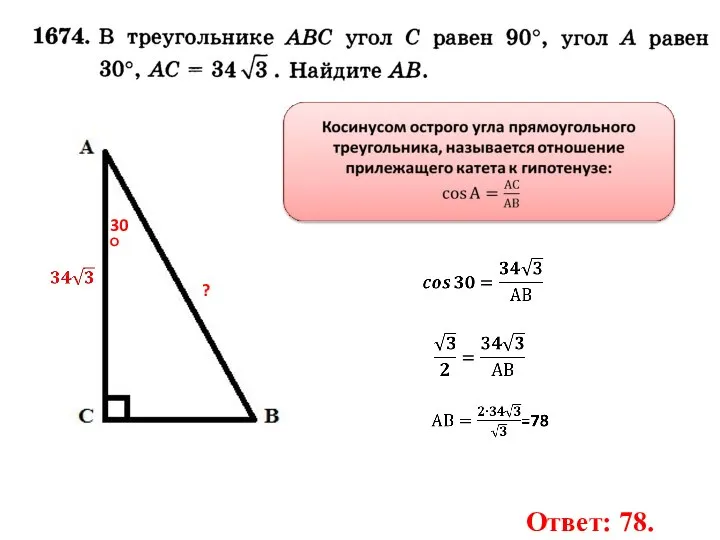
- 3. 30О ? Ответ: 78.
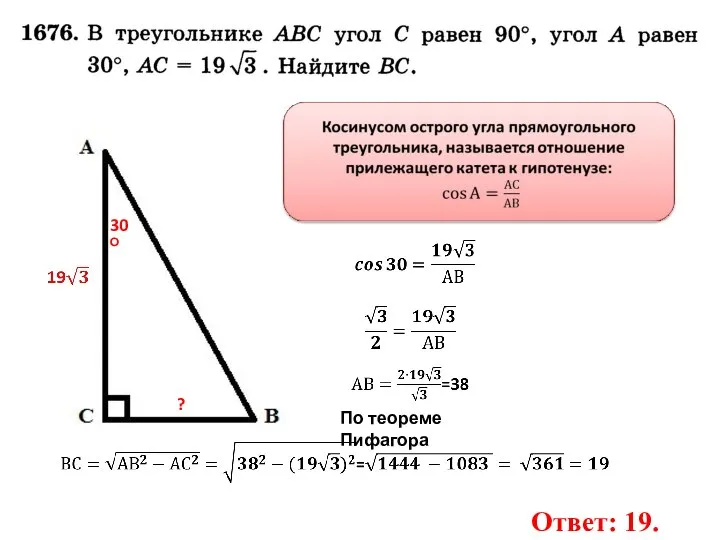
- 4. 30О ? Ответ: 19. По теореме Пифагора
- 5. 30О ? Катет, лежащий напротив угла в 30о, равен половине гипотенузе. По теореме Пифагора Ответ: 150.
- 6. 60О ? Ответ: 100.
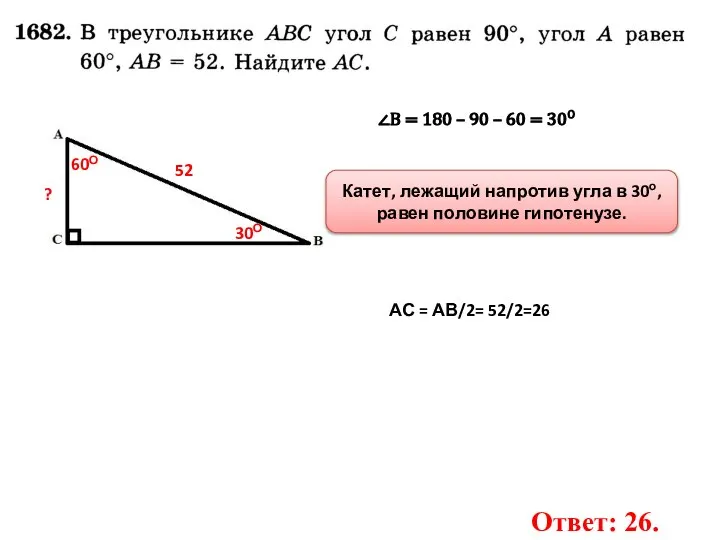
- 7. 60О ? 52 ∠В = 180 – 90 – 60 = 30О 30О Катет, лежащий напротив
- 8. 40 9 Теорема Пифагора Квадрат гипотенузы равен сумме квадратов катетов. Ответ: 41.
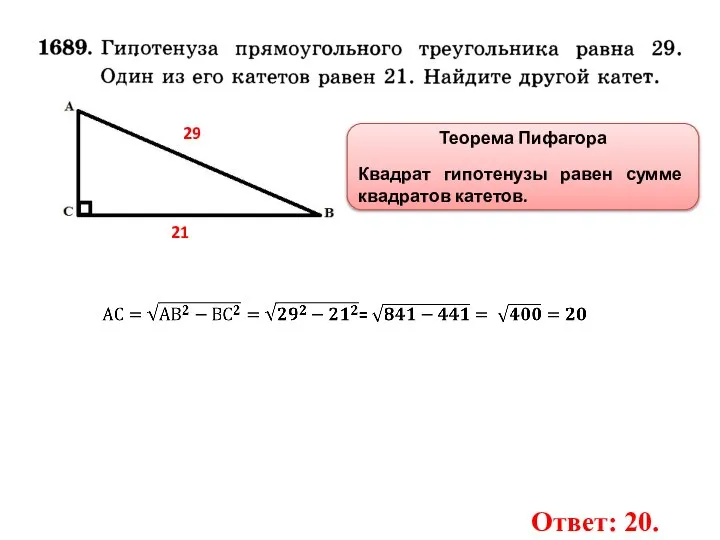
- 9. 21 29 Теорема Пифагора Квадрат гипотенузы равен сумме квадратов катетов. Ответ: 20.
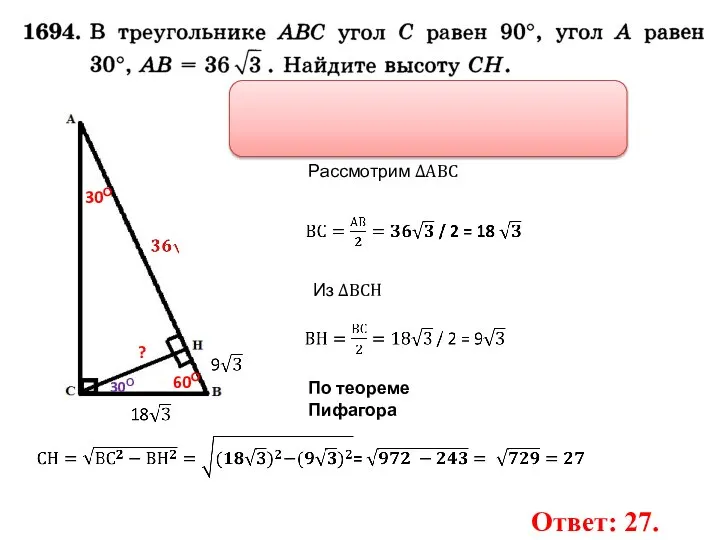
- 10. 30О ? 60О 30О По теореме Пифагора Ответ: 27. Рассмотрим ∆АВС Из ∆ВСН
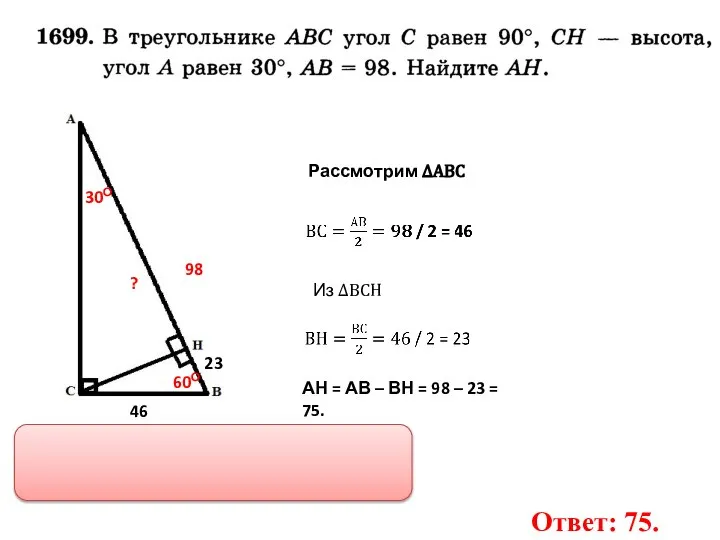
- 11. 30О ? 98 60О 23 46 АН = АВ – ВН = 98 – 23 =
- 12. 30О ? 98 60О 46 Рассмотрим ∆АВС Из ∆ВСН Ответ: 75.
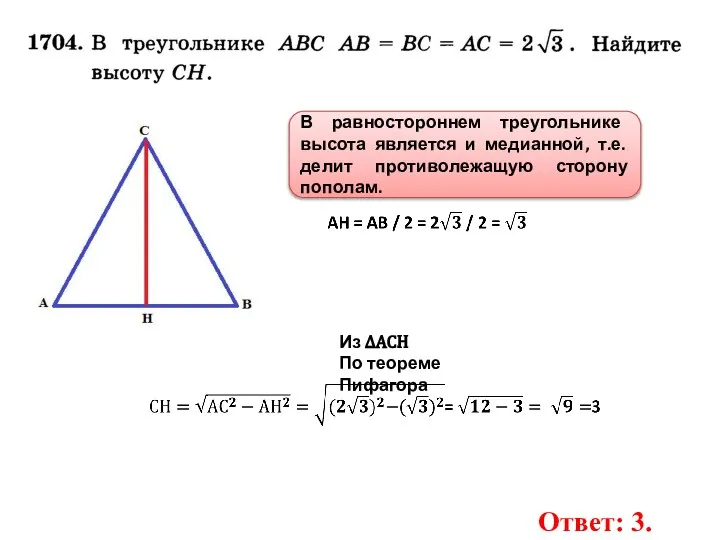
- 13. В равностороннем треугольнике высота является и медианной, т.е. делит противолежащую сторону пополам. Ответ: 3. Из ∆АСН
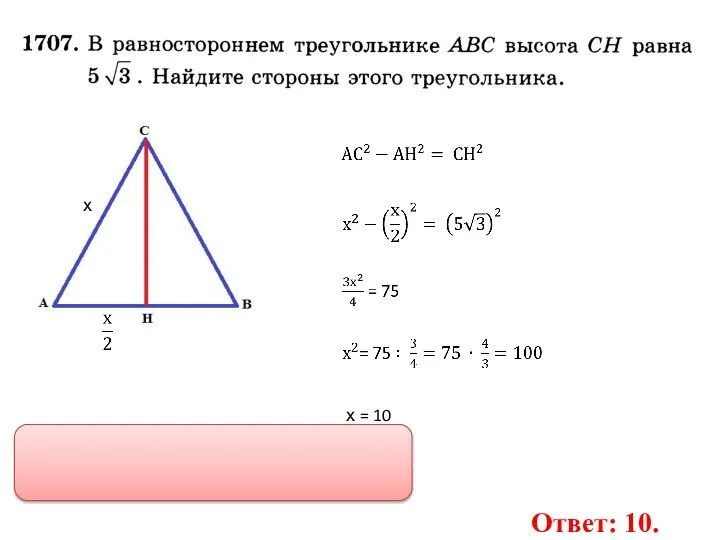
- 14. х х = 10 Ответ: 10.
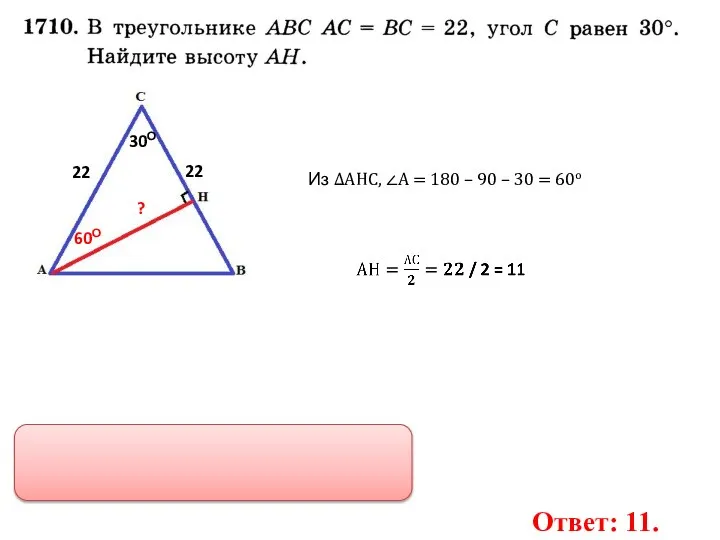
- 15. 30О 22 22 ? Из ∆АНС, ∠А = 180 – 90 – 30 = 60о 60О
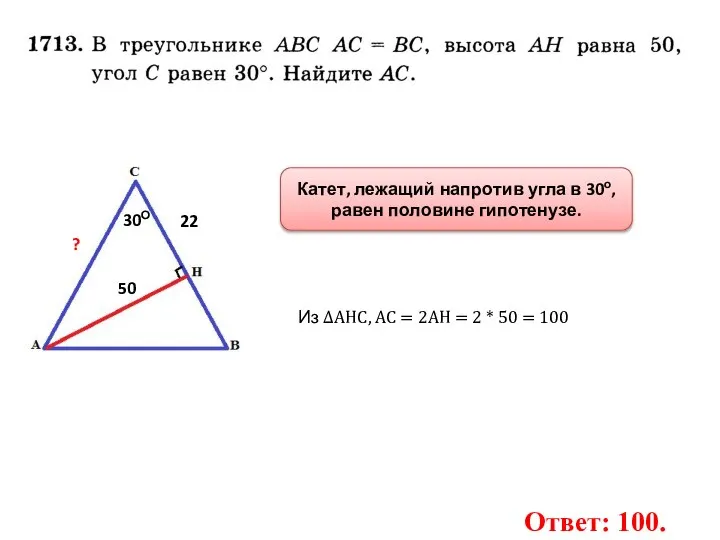
- 16. 30О 22 50 ? Из ∆АНС, АС = 2АН = 2 * 50 = 100 Катет,
- 17. 60О 42 Диагонали прямоугольника равны, АС = AD. Диагонали пересекаясь делятся пополам, АО=ВО=СО=DО. В ∆АОВ, ∠В
- 18. Периметр – сумма длин всех сторон многоугольника. х х + 8 х + 8 х х
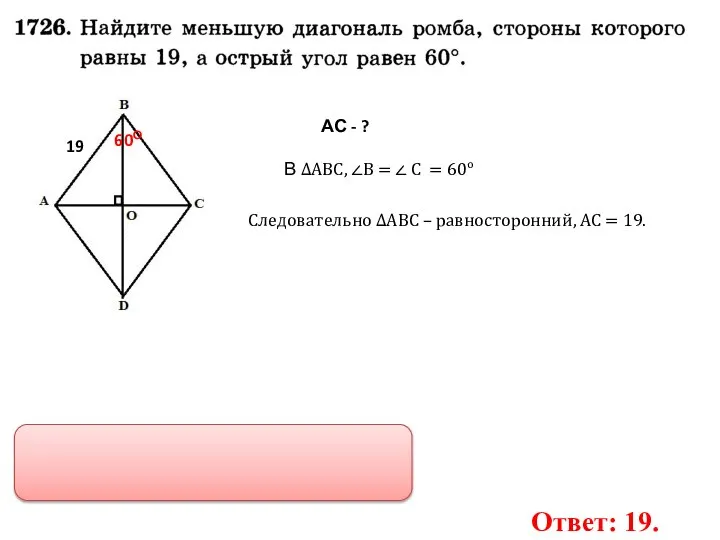
- 19. АС - ? 19 60О В ∆АВС, ∠В = ∠ С = 60о Следовательно ∆АВС –
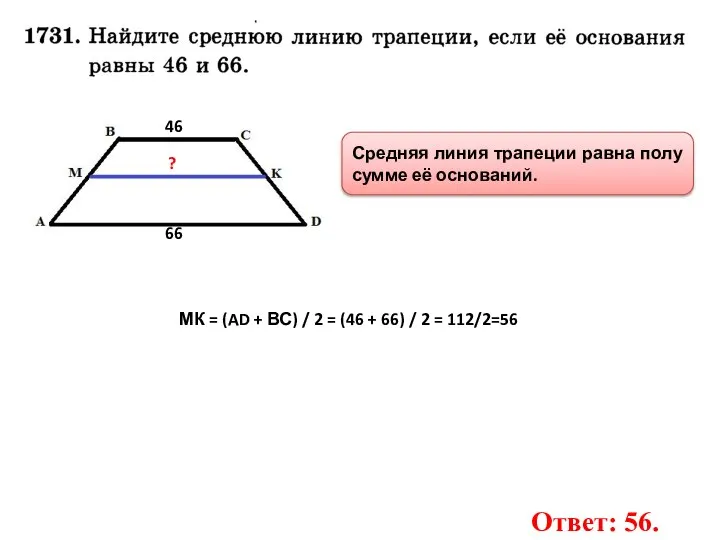
- 20. 46 66 ? Средняя линия трапеции равна полу сумме её оснований. МК = (AD + ВС)
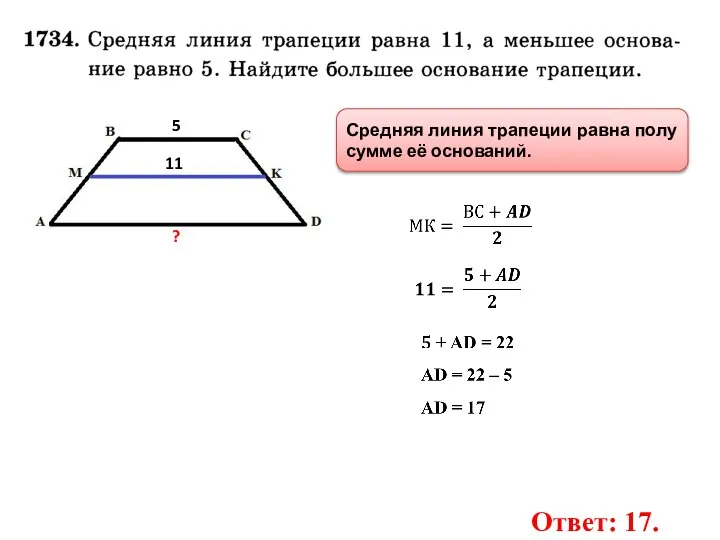
- 21. 5 ? 11 Ответ: 17. Средняя линия трапеции равна полу сумме её оснований.
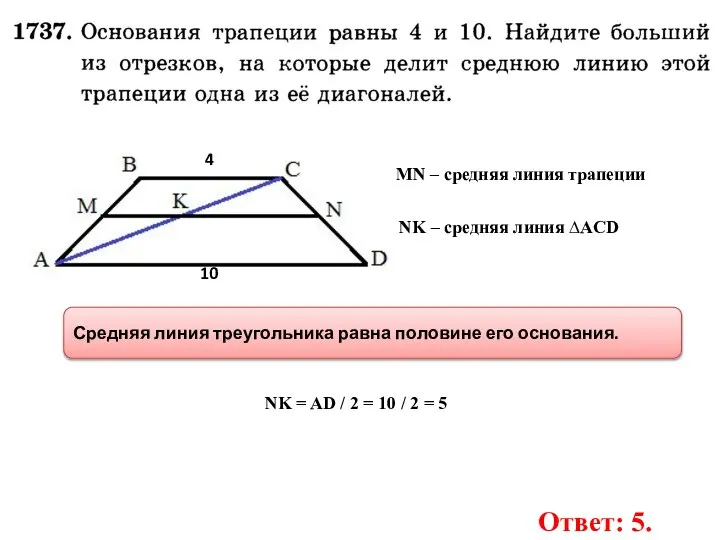
- 22. 4 10 NK – средняя линия ∆ACD NK = AD / 2 = 10 / 2
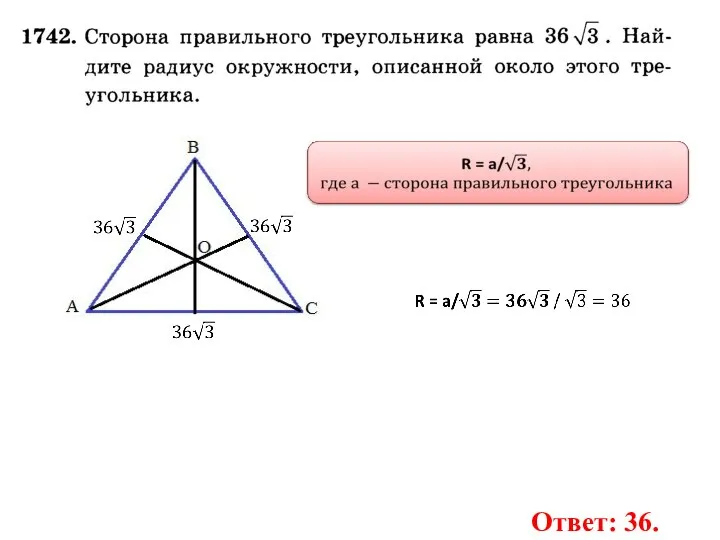
- 23. Ответ: 36.
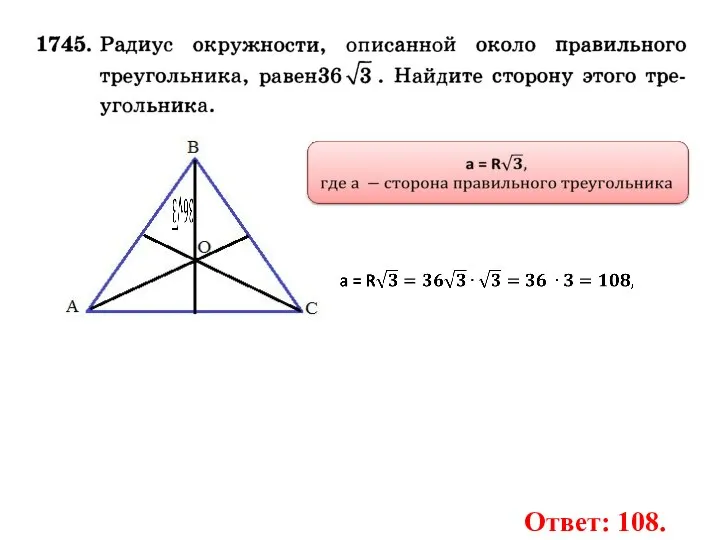
- 24. Ответ: 108.
- 25. 90
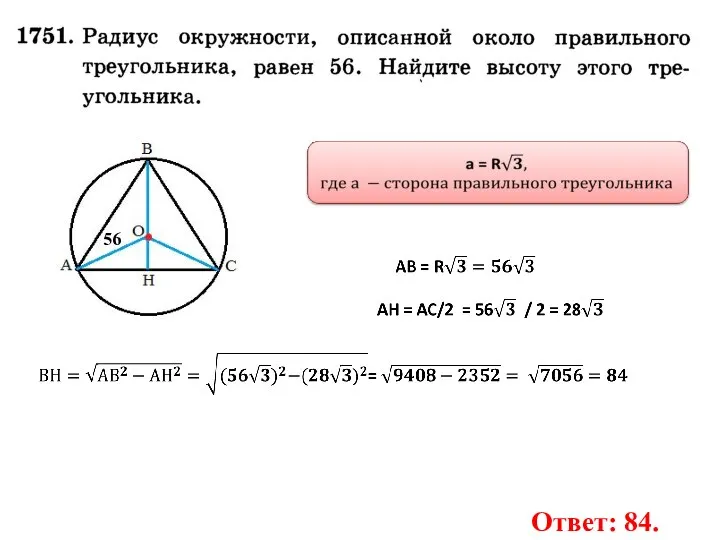
- 26. 56 Ответ: 84.
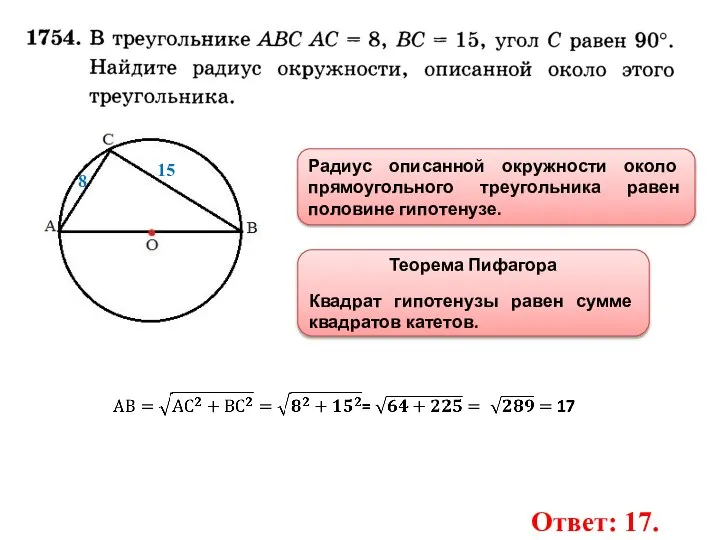
- 27. Радиус описанной окружности около прямоугольного треугольника равен половине гипотенузе. 8 15 Теорема Пифагора Квадрат гипотенузы равен
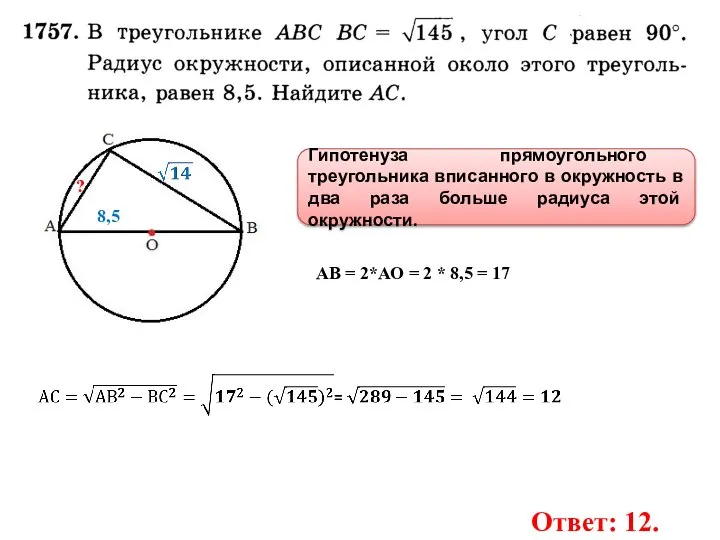
- 28. 8,5 ? Гипотенуза прямоугольного треугольника вписанного в окружность в два раза больше радиуса этой окружности. Ответ:
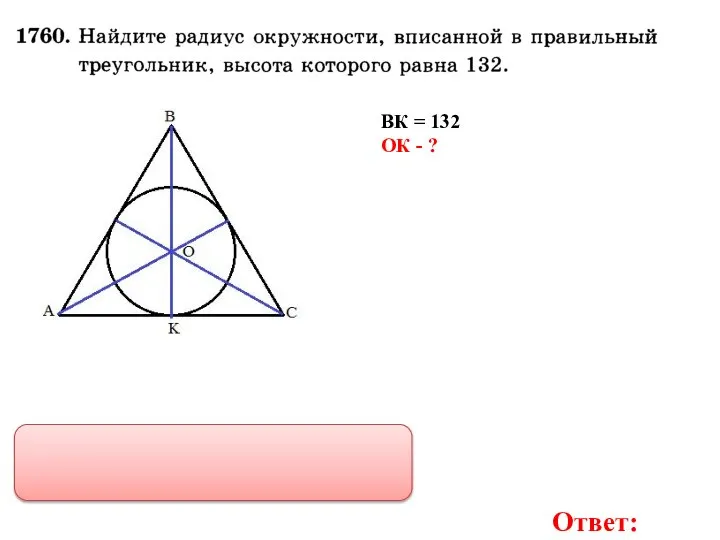
- 29. Ответ: ВК = 132 ОК - ?
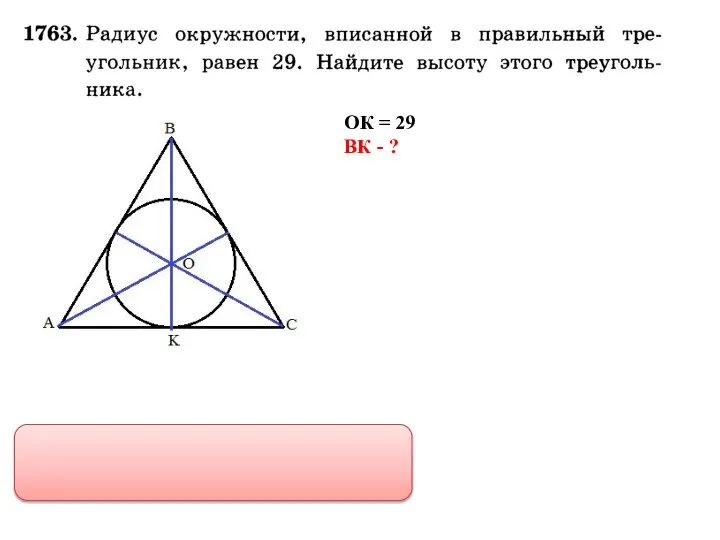
- 30. ОК = 29 ВК - ?
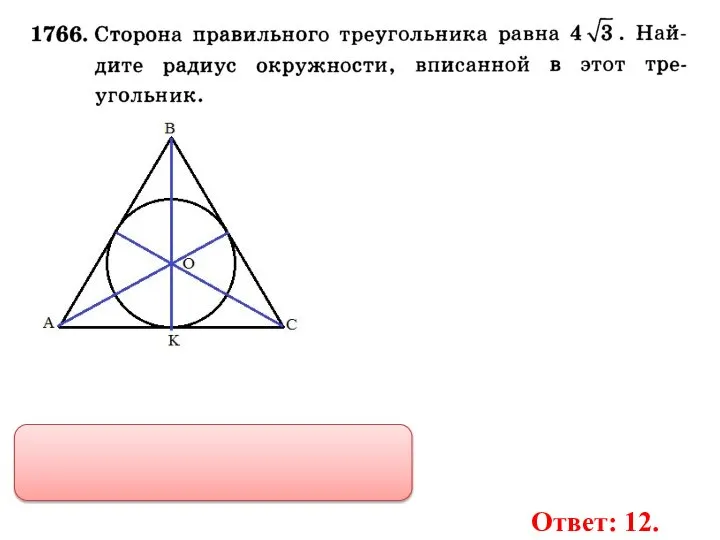
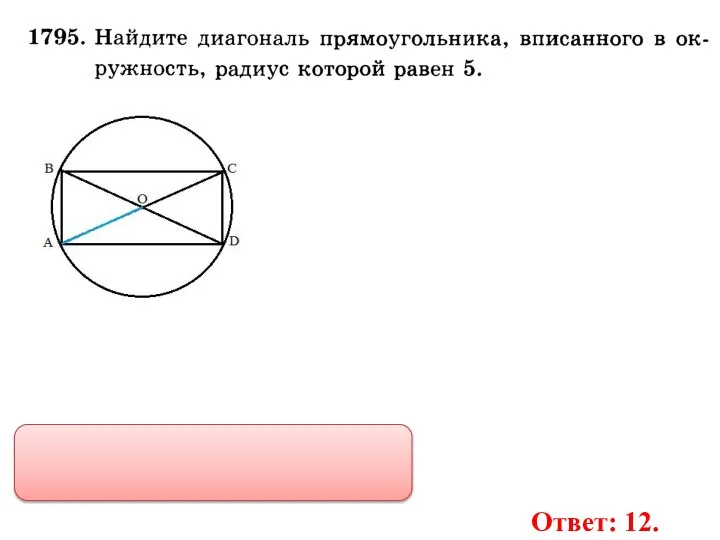
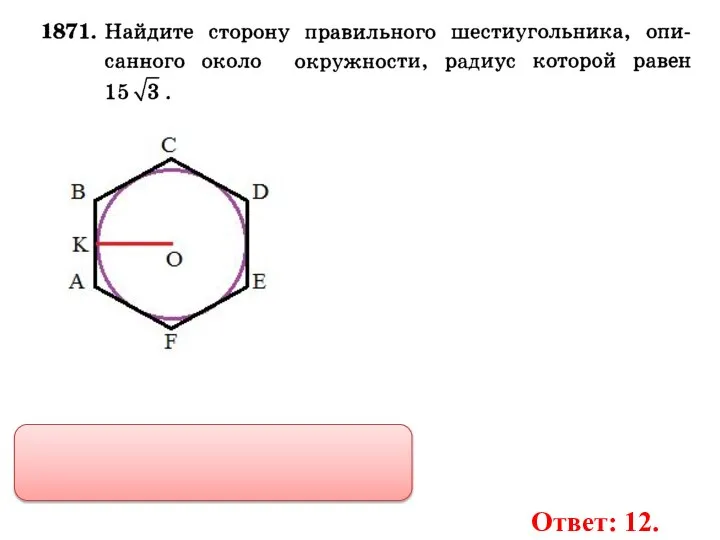
- 31. Ответ: 12.
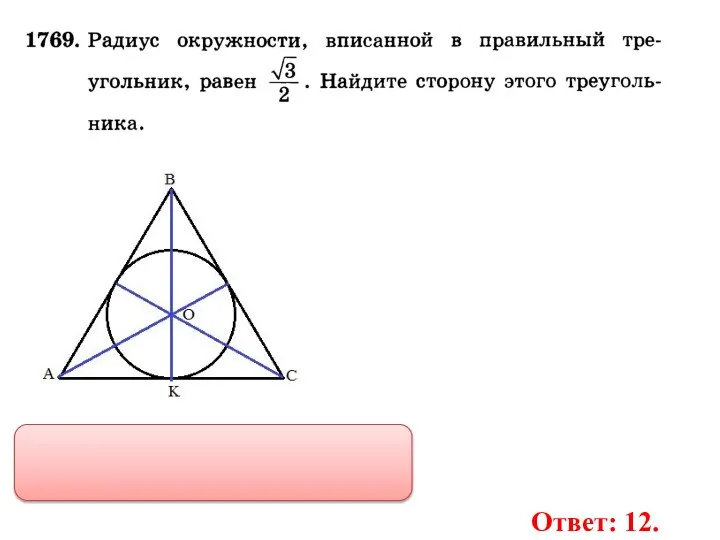
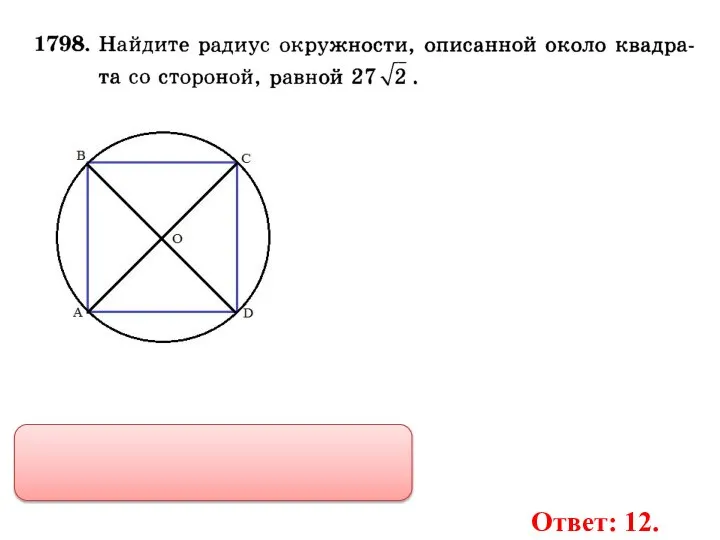
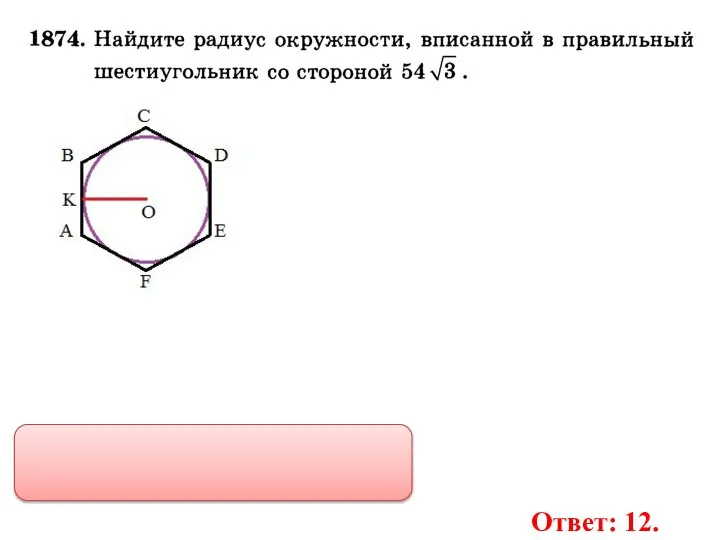
- 32. Ответ: 12.
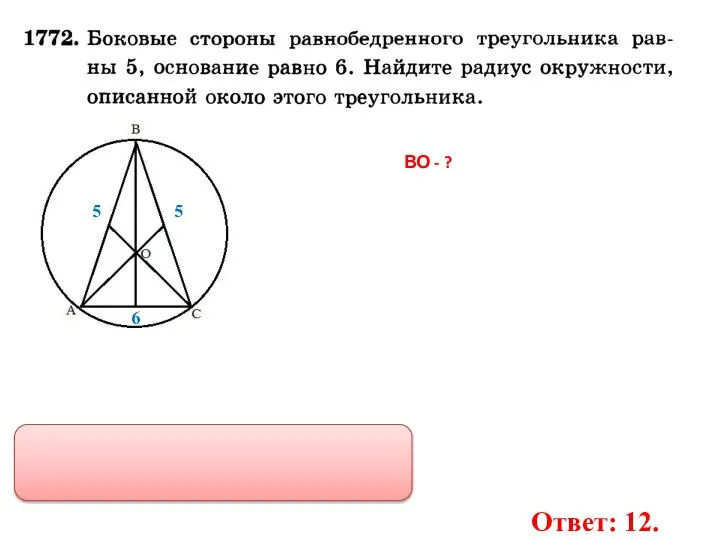
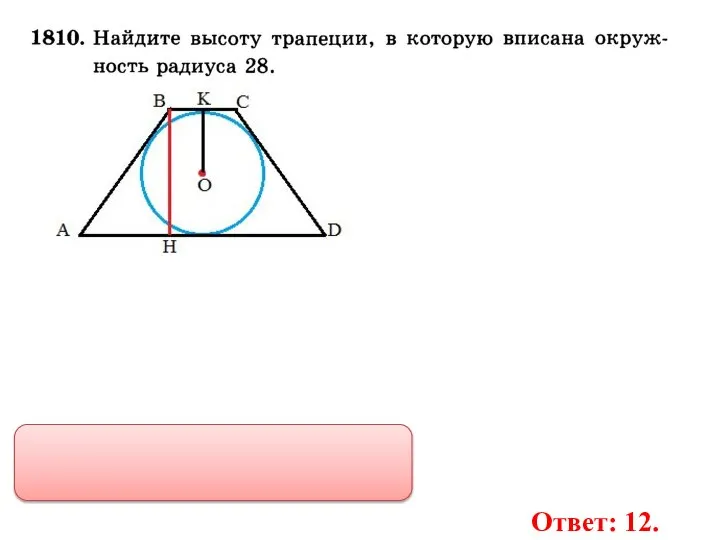
- 33. 5 5 6 ВО - ? Ответ: 12.
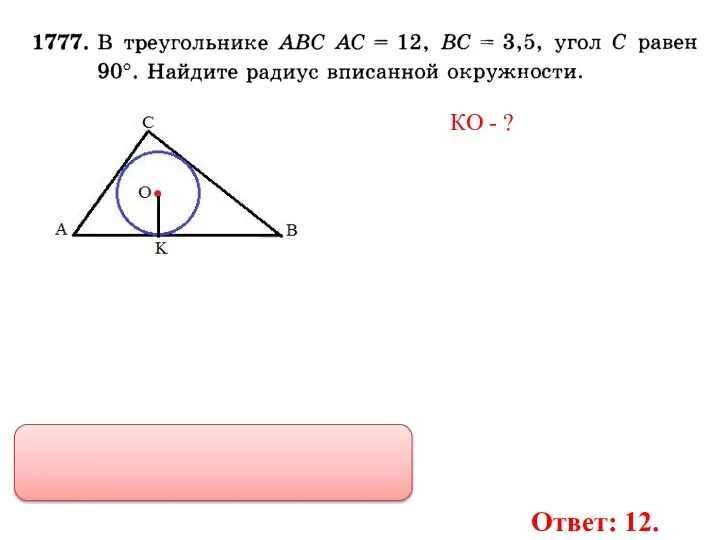
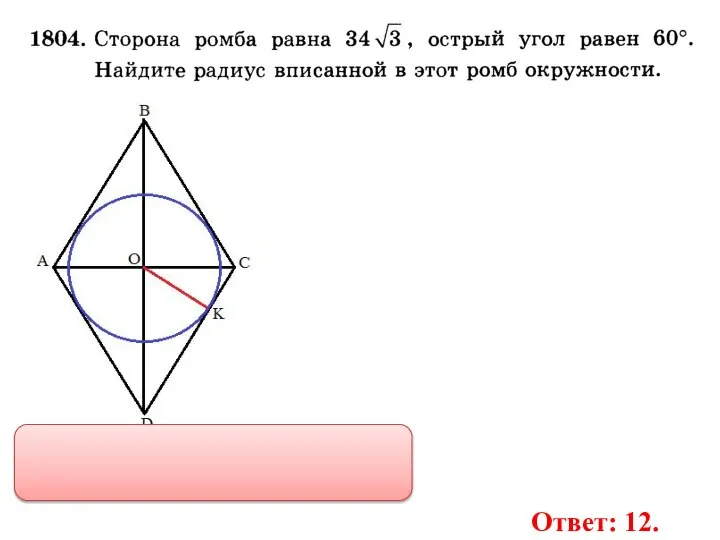
- 34. КО - ? Ответ: 12.
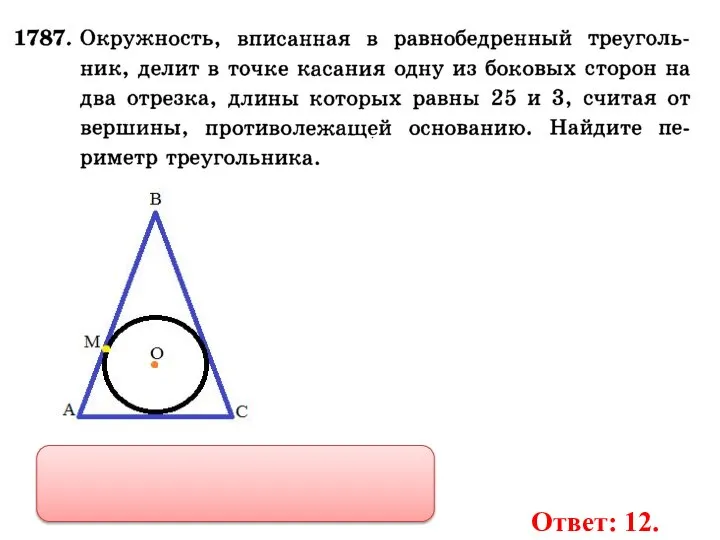
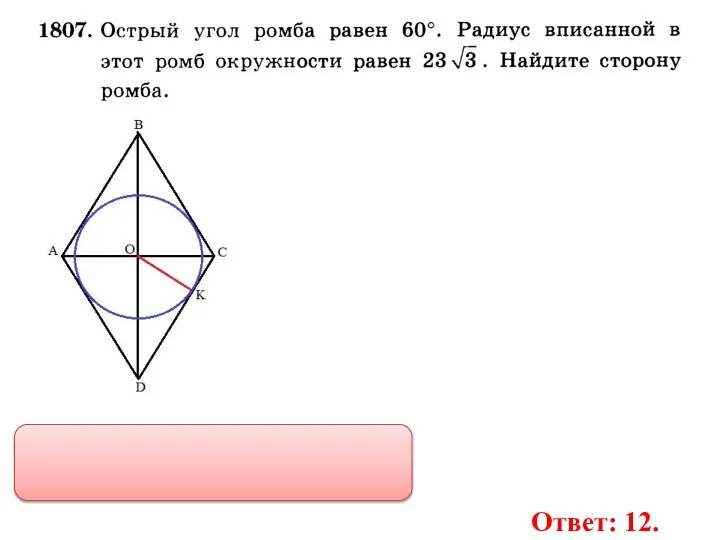
- 35. Ответ: 12.
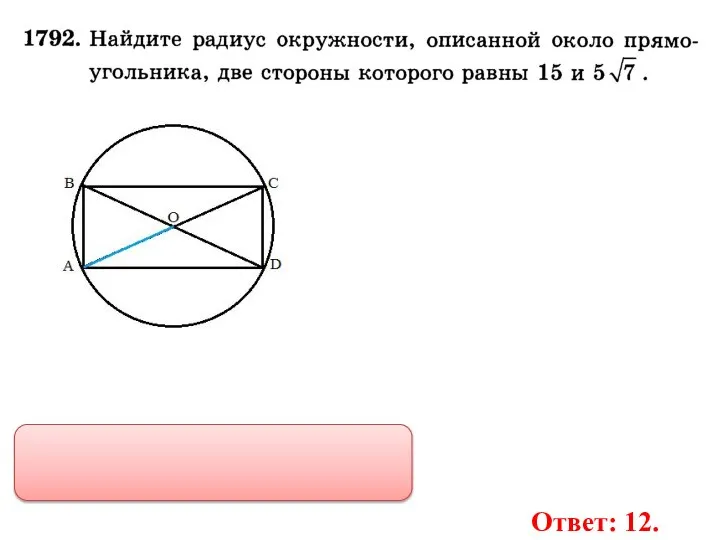
- 36. Ответ: 12.
- 37. Ответ: 12.
- 38. Ответ: 12.
- 39. Ответ: 12.
- 40. Ответ: 12.
- 41. Ответ: 12.
- 42. Ответ: 12.
- 43. Ответ: 12.
- 44. Ответ: 12.
- 45. Ответ: 12.
- 46. Ответ: 12.
- 47. Ответ: 12.
- 48. Ответ: 12.
- 49. Ответ: 12.
- 50. Ответ: 12.
- 51. Ответ: 12.
- 52. Ответ: 12.
- 53. Ответ: 12.
- 54. Ответ: 12.
- 55. Ответ: 12.
- 56. Ответ: 12.
- 57. Ответ: 12.
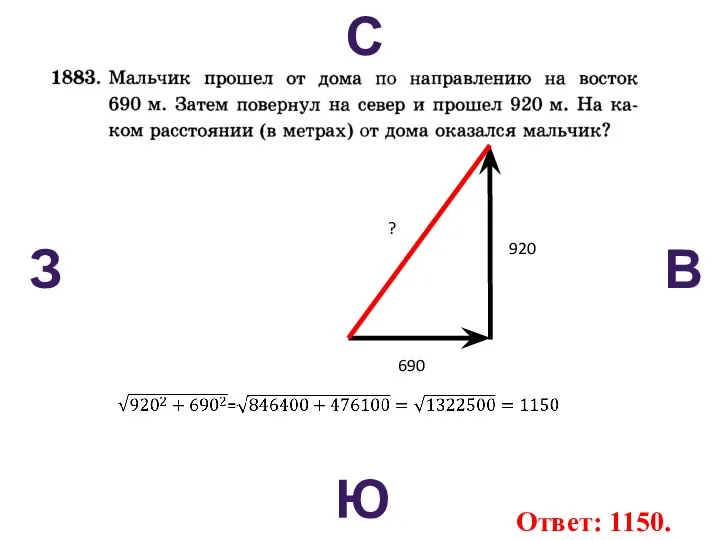
- 59. С В Ю З 690 920 ? Ответ: 1150.
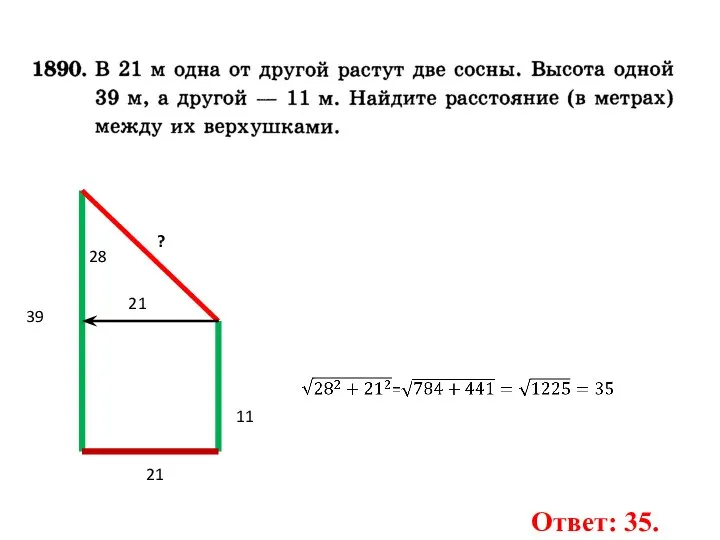
- 60. 11 39 ? 21 28 21 Ответ: 35.
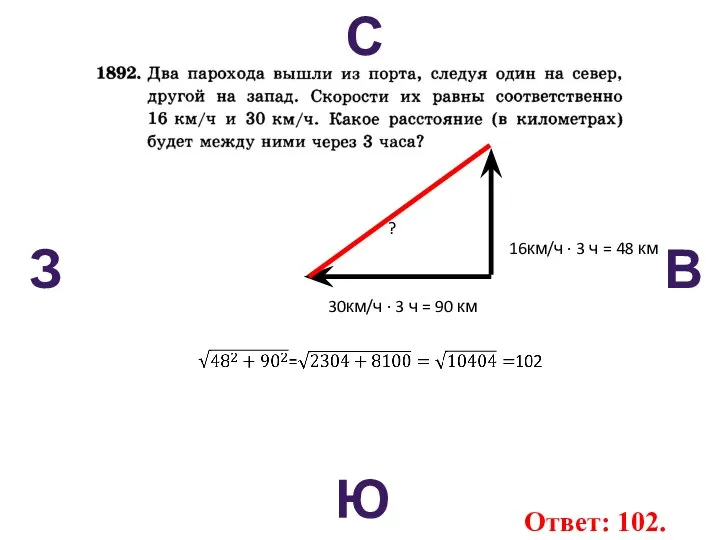
- 61. С В Ю З 30км/ч · 3 ч = 90 км 16км/ч · 3 ч =
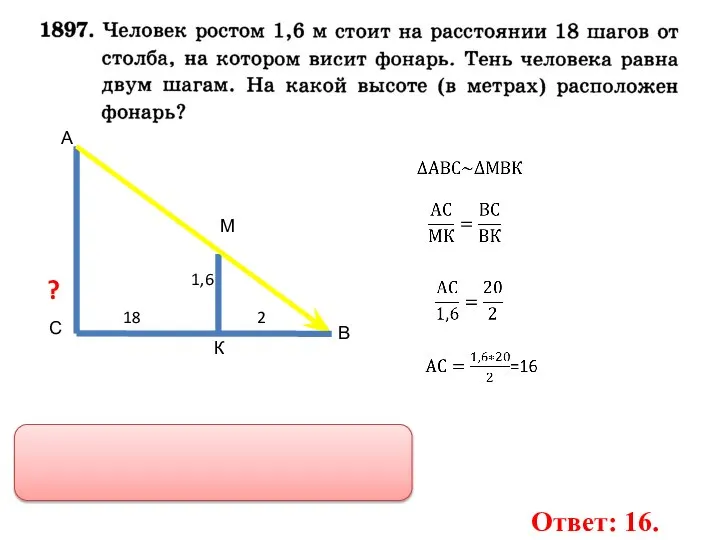
- 62. 18 1,6 2 ? А М В С К Ответ: 16.
- 64. Скачать презентацию


















 Ромб: признаки и свойства
Ромб: признаки и свойства 3
3 Параллелограм и трапеция
Параллелограм и трапеция Прямая пропорциональность и ее график
Прямая пропорциональность и ее график Общие методы решения уравнений
Общие методы решения уравнений Исследование применения математического аппарата сетей Петри для моделирования процесса распределения инцидентов ИТ-службы
Исследование применения математического аппарата сетей Петри для моделирования процесса распределения инцидентов ИТ-службы Компьютерное моделирование процесса подготовки РКН к пуску. Лекция 15
Компьютерное моделирование процесса подготовки РКН к пуску. Лекция 15 Свойства натурального ряда чисел
Свойства натурального ряда чисел Вписанная и описанная окружность. 9 класс
Вписанная и описанная окружность. 9 класс Линейные неравенства
Линейные неравенства Ознакомление с задачей в 2 действия
Ознакомление с задачей в 2 действия Перестановочные тесты и бутстреп анализ
Перестановочные тесты и бутстреп анализ В мире случайных закономерностей. Введение в вероятность. 5 класс
В мире случайных закономерностей. Введение в вероятность. 5 класс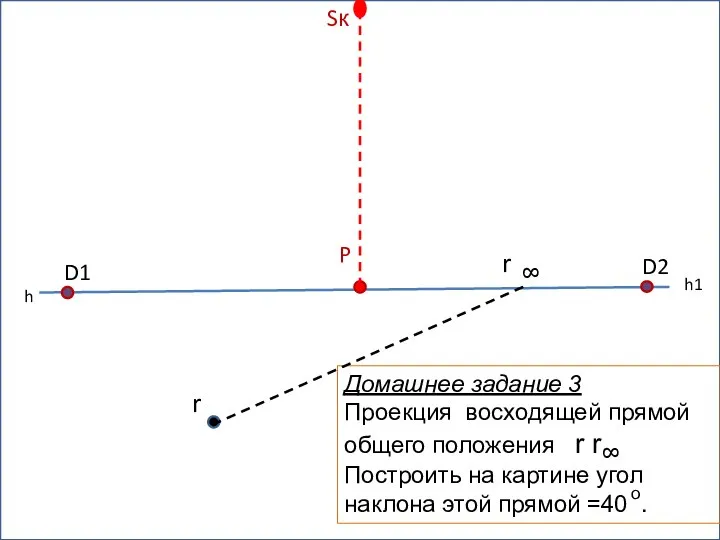 Проекция восходящей прямой общего положения r r
Проекция восходящей прямой общего положения r r Математика вокруг нас. Геометрические узоры и орнамент на посуде
Математика вокруг нас. Геометрические узоры и орнамент на посуде Многочлен и его стандартный вид
Многочлен и его стандартный вид Пересечение высот
Пересечение высот Решение задач по теме Соотношения между сторонами и углами в прямоугольном треугольнике
Решение задач по теме Соотношения между сторонами и углами в прямоугольном треугольнике Презентация на тему Площадь круга и длина окружности
Презентация на тему Площадь круга и длина окружности  Переместительное свойство умножения
Переместительное свойство умножения 797821
797821 Угол. Расстояние
Угол. Расстояние Функция у=arccos x
Функция у=arccos x Площадь криволинейной трапеции
Площадь криволинейной трапеции Ãkom Erikom do 100
Ãkom Erikom do 100 Подготовка к ЕГЭ (профильный уровень). Теория вероятности
Подготовка к ЕГЭ (профильный уровень). Теория вероятности Диагностика и развитие мышления школьников на уроках математики
Диагностика и развитие мышления школьников на уроках математики Сложение чисел. Как можно найти значение суммы 7 + 7
Сложение чисел. Как можно найти значение суммы 7 + 7