Содержание
- 2. I. Факториал Факториал числа n (n!) — произведение всех натуральных чисел от 1 до n включительно
- 3. Таблица факториалов 16! = 20922789888000 17! = 355687428096000 18! = 6402373705728000 19! = 121645100408832000 20! =
- 4. II. Решение задач #1. Вычислить: #2. #3. Делится ли 11! на 49? Ответ: нет
- 5. #4. Сколькими нулями оканчивается число 26! Ответ: 6 #5. Сократить дробь
- 6. #6. Упростить выражение
- 7. #7. Решить уравнение
- 8. III. Перестановки Перестановки из n элементов - это комбинации из n элементов, отличающиеся друг от друга
- 9. IV. Решение задач «Проказница-Мартышка, Осел, Козел Да косолапый Мишка Затеяли сыграть Квартет. Достали нот, баса, альта,
- 10. Сколькими способами можно развесить 5 цветных шаров на гирлянде? Решение: Р5 = 5! = 1·2·3·4·5= 120
- 11. Задача №3. В расписании 9 класса на четверг должно быть 6 предметов: русский язык, литература, алгебра,
- 12. Задача 6. Сколько различных 5-значных чисел, все цифры которых различны можно записать с помощью цифр 4,
- 13. V. Обобщения факториала 1. Двойной факториал числа n - обозначается n!! - произведение всех натуральных чисел
- 14. 2. Праймориал (примориал) числа n - обозначается n# - произведение простых чисел, не превышающих n. 11#
- 16. Скачать презентацию

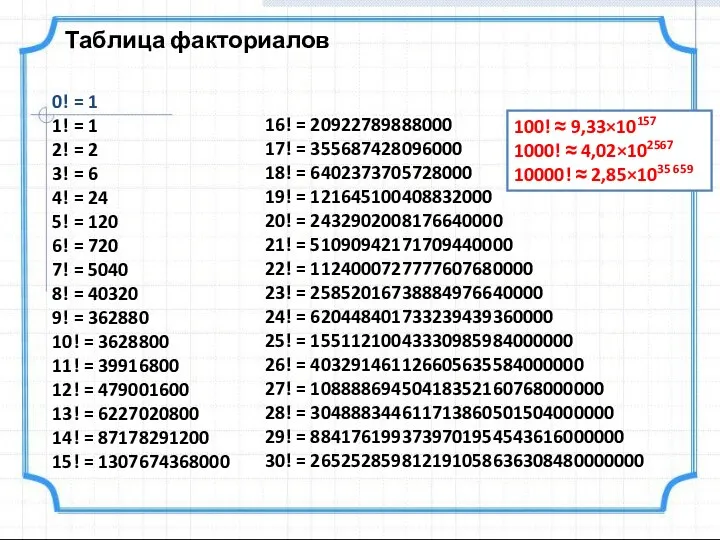











 Схема Горнера
Схема Горнера Индивидуальное задание №8. Построение линии пересечения тора и конуса
Индивидуальное задание №8. Построение линии пересечения тора и конуса Математика в играх и задачах
Математика в играх и задачах Призмы и антипризмы
Призмы и антипризмы Степенная функция и ее график
Степенная функция и ее график Задачи на перебор вариантов. 4 класс
Задачи на перебор вариантов. 4 класс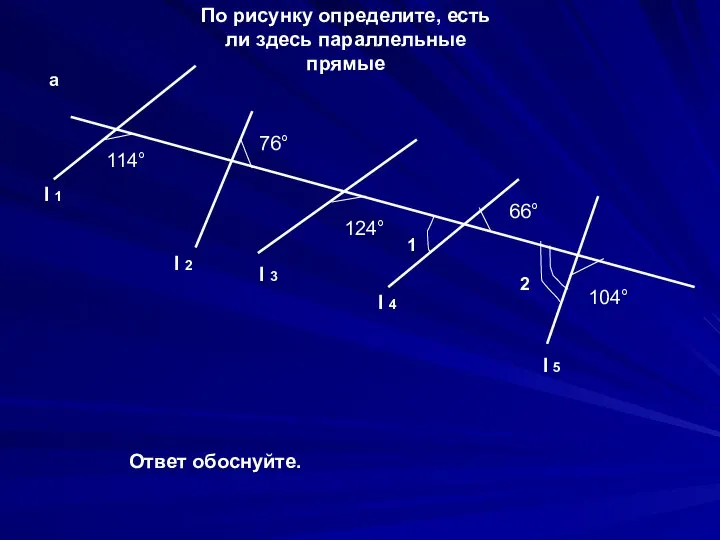 Параллельные прямые
Параллельные прямые Решение уравнений с помощью разложения на множители
Решение уравнений с помощью разложения на множители Предельные величины, эластичности
Предельные величины, эластичности Несобственные интегралы. Лекция 5
Несобственные интегралы. Лекция 5 Круглые числа. Величина
Круглые числа. Величина Задача на тему: Прогрессия
Задача на тему: Прогрессия Системы линейных дифференциальных уравнений
Системы линейных дифференциальных уравнений Системы линейных алгебраических уравнений (СЛАУ)
Системы линейных алгебраических уравнений (СЛАУ) Презентация на тему Призма
Презентация на тему Призма  predel-posledovatelnosti-svoystva-i
predel-posledovatelnosti-svoystva-i Абсолютная величина
Абсолютная величина Своя игра. Показательная и степенная функции. 10 класс
Своя игра. Показательная и степенная функции. 10 класс Куб. Теорема Эйлера
Куб. Теорема Эйлера Сложение и вычитание положительных и отрицательных чисел
Сложение и вычитание положительных и отрицательных чисел Великолепная пятерка. Игра
Великолепная пятерка. Игра 2._3
2._3 Презентация на тему Решение экспериментальных задач
Презентация на тему Решение экспериментальных задач  Арифметика в позиционных системах счисления
Арифметика в позиционных системах счисления Длина. Сантиметр
Длина. Сантиметр Дифференциальные уравнения. Лекция 2
Дифференциальные уравнения. Лекция 2 Измерение углов. Транспортир
Измерение углов. Транспортир Умножение десятичной дроби на обыкновенную
Умножение десятичной дроби на обыкновенную