Содержание
- 2. Проверка ДЗ
- 3. Проверка ДЗ
- 4. Проверка ДЗ
- 5. Решите квадратные уравнения
- 6. ЛОДУ 2 порядка с постоянными коэффициентами Общий вид: у – искомая функция; p, g – постоянные
- 7. ЛОДУ 2 порядка с постоянными коэффициентами 1) Заменяем k - некоторое число Алгоритм: 2) Находим производные
- 8. Если (действительные числа), то общее решение однородного уравнения имеет вид: Если (действительные числа) то общее решение
- 9. Пример 1: Найдите общее решение дифференциального уравнения (Заменяем) (Подставляем в уравнение) (Решаем квадратное уравнение) (Подставляем в
- 10. Пример 2: Найдите общее решение дифференциального уравнения (Заменяем) (Подставляем в уравнение) (Решаем квадратное уравнение) (Подставляем в
- 11. Пример 3: Найдите общее решение дифференциального уравнения (Заменяем) (Подставляем в уравнение) (Решаем квадратное уравнение) (Подставляем в
- 13. Скачать презентацию










 Алгоритмы на графах
Алгоритмы на графах Числовые и буквенные выражения
Числовые и буквенные выражения Степень с рациональным показателем. Самостоятельная работа
Степень с рациональным показателем. Самостоятельная работа Векторы (повторение). 8 класс
Векторы (повторение). 8 класс арифметическая прогрессия. Решение задач. 9 класс
арифметическая прогрессия. Решение задач. 9 класс Презентация на тему Единицы массы. Тонна. Центнер (4 класс)
Презентация на тему Единицы массы. Тонна. Центнер (4 класс)  Подготовка к к/р
Подготовка к к/р Презентация на тему Медиана
Презентация на тему Медиана  Геометрический конструктор: Развивающая игра Танграм
Геометрический конструктор: Развивающая игра Танграм Системы линейных алгебраических уравнений. Лекция 3а
Системы линейных алгебраических уравнений. Лекция 3а Признаки и свойства папаллельных и перпендикулярных плоскостей
Признаки и свойства папаллельных и перпендикулярных плоскостей Площади геометрических фигур
Площади геометрических фигур Многоугольники
Многоугольники Площадь фигуры. Единицы площади. Самостоятельная работа
Площадь фигуры. Единицы площади. Самостоятельная работа Геометрия вокруг нас
Геометрия вокруг нас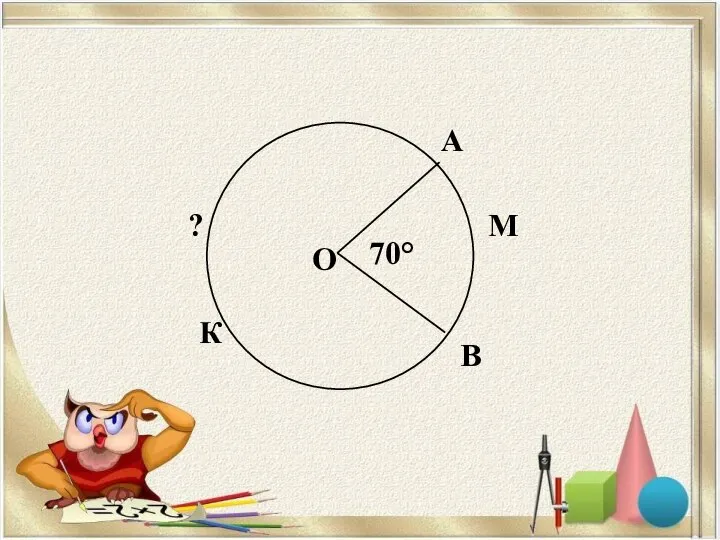 Окружность. Вписанные и описанные углы
Окружность. Вписанные и описанные углы Вписанный угол
Вписанный угол Системы линейных уравнений
Системы линейных уравнений Мой класс в диаграммах и цифрах
Мой класс в диаграммах и цифрах Геометрический смысл производной
Геометрический смысл производной Методическая разработка урока геометрии по теме Окружность
Методическая разработка урока геометрии по теме Окружность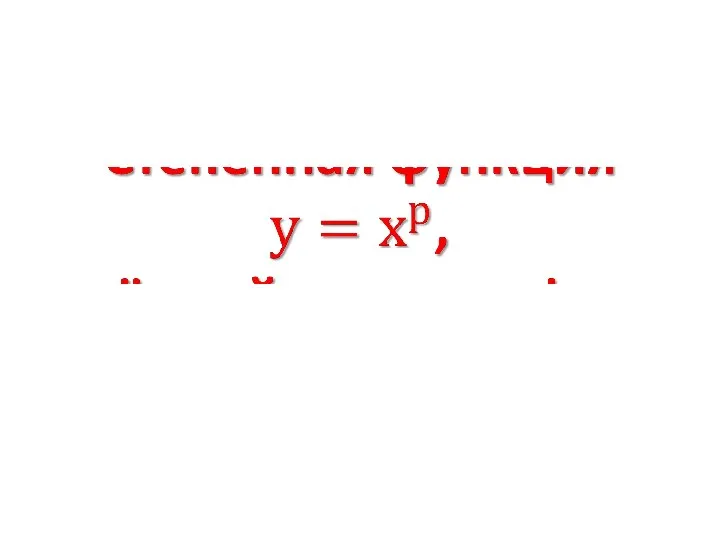 Степенная функция и её график
Степенная функция и её график Задачі_на_наслідки_із_аксіом_стереометрії
Задачі_на_наслідки_із_аксіом_стереометрії Свойство противоположных сторон прямоугольника
Свойство противоположных сторон прямоугольника Разложение вектора
Разложение вектора Теория графов
Теория графов Занятие 1_2022
Занятие 1_2022 Сопоставимость показателей. Лекция 2
Сопоставимость показателей. Лекция 2