Дифференциальные уравнения

При изучении явлений природы, решении многих задач физики и техники, химии и биологии, других наук не всегда удается непосредственно установить прямую зависимость между величинами, описывающими тот или иной процесс. Однако в большинстве случаев можно установить связь между величинами (функциями) и скоростями их изменения относительно других (независимых) переменных величин, т.е. найти уравнения, в которых неизвестные функции входят под знак производной. Эти уравнения называют дифференциальными.
I.Введение

II.Основная часть
Простейшим примером дифференциального уравнения является уравнение
где f(x) – известная функция, а y=y(x) – искомая функция независимого переменного x.
Теоретическая часть
Решения этого уравнения называют первообразными функциями для функции f(x). Например, решениями дифференциального уравнения
являются функции
С – произвольная постоянная, причем других решений это уравнение не имеет.

Характерное свойство дифференциальных уравнений – иметь бесконечное множество решений. В этом смысле приведенный выше пример типичен. Поэтому, решив дифференциальное уравнение, описывающее эволюцию некоторого процесса, нельзя одновременно найти зависимость между величинами, характеризующими данный процесс.
Чтобы выделить из бесконечного множества зависимостей ту, которая описывает именно этот процесс, надо иметь дополнительную информацию, например знать начальное состояние процесса. Без этого дополнительного условия задача недоопределенна.
Рассмотрим несколько конкретных задач, приводящих к дифференциальным уравнениям

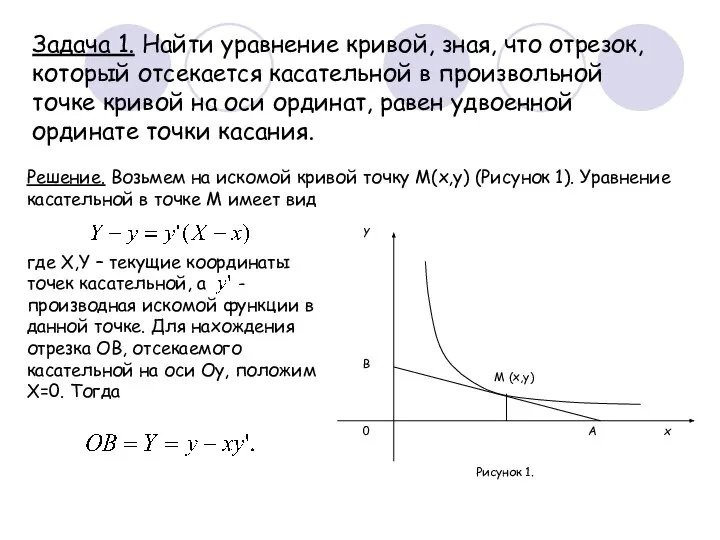
Решение. Возьмем на искомой кривой точку M(x,y) (Рисунок 1). Уравнение касательной в точке М имеет вид
Задача 1. Найти уравнение кривой, зная, что отрезок, который отсекается касательной в произвольной точке кривой на оси ординат, равен удвоенной ординате точки касания.
где Х,Y – текущие координаты точек касательной, а - производная искомой функции в данной точке. Для нахождения отрезка ОВ, отсекаемого касательной на оси Oy, положим Х=0. Тогда

Умножив обе части этого уравнения на , приведем его к виду, содержащему дифференциалы,
(2)
Левая часть уравнения (2) представляет собой дифференциал произведения переменных d(xy), поэтому уравнение (2) можно записать в виде
откуда
(3)
где С – произвольное постоянное. Равенство (3) дает уравнение искомой кривой, которое также можно записать и в явном виде
(4)
С другой стороны, по условию задачи OB=2y; сравнивая оба выражения для отрезка OB, получаем уравнение
или
(1)

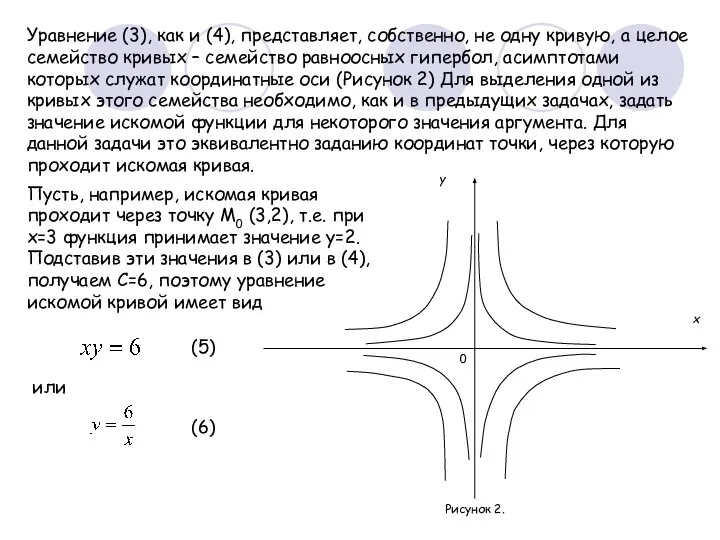
Уравнение (3), как и (4), представляет, собственно, не одну кривую, а целое семейство кривых – семейство равноосных гипербол, асимптотами которых служат координатные оси (Рисунок 2) Для выделения одной из кривых этого семейства необходимо, как и в предыдущих задачах, задать значение искомой функции для некоторого значения аргумента. Для данной задачи это эквивалентно заданию координат точки, через которую проходит искомая кривая.
Пусть, например, искомая кривая проходит через точку M0 (3,2), т.е. при х=3 функция принимает значение у=2. Подставив эти значения в (3) или в (4), получаем С=6, поэтому уравнение искомой кривой имеет вид
(5)
или
(6)

Задача2. Определить давление воздуха в зависимости от высоты над уровнем моря.
Рассмотрим горизонтальную площадку размером 1 м2, расположенную на уровне моря, и призматический столб воздуха, опирающийся на эту площадку. Если мысленно провести сечение столба на высоте h (Рисунок 3), то давление в этом сечении определяется весом части столба, находящейся над сечением. Проведем второе горизонтальное сечение на высоте h+∆h.
Решение. Обозначим высоту над уровнем моря через h и давление воздуха через p. Задача состоит в том, чтобы отыскать функцию p=p(h), описывающую зависимость давления от высоты.

где s – вес одного кубометра воздуха при давлении p. Но величина s сама пропорциональна давлению. Действительно, пусть s0 – вес кубометра воздуха при давлении p0=1.
Давление в этом сечении будет меньше на величину ∆p, равную весу воздуха в столбе между двумя сечениями. Поэтому можно написать ,
В силу закона Бойля-Мариотта (pV=p0V0) это же количество воздуха будет при давлении p занимать объём
кубометров и весить
по-прежнему s0. Вес s одного кубометра будет тогда равен
или вообще
где k – коэффициент пропорциональности. Таким образом получаем соотношение:
(7)

Равенство (7) является неточным: здесь предположено, что во всех сечениях между h и h+∆h давление постоянно и равно p. На самом же деле давление в этих сечениях различно и падает с увеличением h. Однако функцию p=p(h) естественно предположить непрерывной, поэтому ошибка равенства (7) невелика и будет тем меньше, чем меньше величина ∆h. Если разделить теперь обе части равенства (7) на ∆h и перейти к пределу при ∆h→0, то ошибка в нем также будет стремиться к нулю, и мы получим уже точное равенство:
(8)
Равенство (8) есть дифференциальное уравнение, связывающее неизвестную (искомую) функцию p(h) и её производную. Решением этого уравнения является функция, выражающая зависимость давления воздуха p от высоты h. Рассмотрим в соотношении (7) высоту h над уровнем моря как функцию от давления p. Так приходится поступать, например, при барометрическом моделировании, когда требуется определять высоту места по показаниям барометра. В этом случае, разделив обе части равенства (7) на ∆p и перейдя к пределу при ∆p→0, получим
или
(9)

Равенство (9) также является дифференциальным уравнением, но здесь мы имеем простейшую зависимость: производная неизвестной функции выражается как известная функция аргумента. Поэтому для нахождения неизвестной функции h остается только взять неопределенный интеграл, после чего находим
(10)
Величина C1 представляет произвольное постоянное интегрирования, которое удобнее для дальнейшего записать в виде . Тогда равенство (4) можно будет переписать так:
(11)
Равенство (11) дает выражение для искомой функции h=h(p), однако это выражение остается не вполне определенным вследствие наличия в нем произвольного постоянного С. Для того, чтобы достичь полной определенности, необходимо знать С, что достигается заданием значения p при каком-либо значении h. В данном случае это удобнее всего сделать, приняв, что на уровне моря (при h=0) атмосферное давление равно p=p0. Подставив эти значения в (11), мы получим С=p0, так что окончательно искомая функция выражается формулой

(12)
Равенство (12) можно разрешить относительно p и тем самым получить решение первоначально поставленной задачи. Выражением давления воздуха p в зависимости от высоты h над уровнем моря определяется формулой
(13)
Итак, давление убывает с высотой по показательному закону в соответствии с полученной так называемой барометрической формулой. Формула (13) на больших высотах (сравнимых по величине с радиусом Земли) дает большую погрешность. Это связано с тем, что пренебрегаем не только изменением температуры, но и изменением ускорения свободного падения.

Задача3. В благоприятных для размножения условиях находится некоторое количество N0 бактерий. Из эксперимента известно, что скорость размножения бактерий пропорциональна их количеству. Найти зависимость роста числа бактерий с течением времени.
Решение. Обозначим через N(t) количество размножающихся бактерий в момент времени t: N(0)=N0. Отвлекаясь от того, что численность может измеряться только целыми числами, считаем, что N(t) изменяется во времени непрерывно дифференцируемо. Тогда скорость размножения есть производная от функции N(t); поэтому указанный в условии задачи биологический экспериментальный закон позволяет составить дифференциальное уравнение размножения бактерий:
k>0
(14)
Коэффициент k зависит от вида бактерий и условий, в которых они находятся. Его можно определить экспериментально.

Задача свелась к чисто математической задаче: найти решение N уравнения (14), для которого N(0)=N0.
Поскольку N(t)>0, разделив обе части уравнения (14) на N(t) и продифференцировав получаем:
(15)
где С1 – произвольная постоянная; обозначим ее так:
,C>0. Из (15) имеем
(16)
Чтобы из множества функций (16) выделить ту, которая описывает процесс размножения бактерий, воспользуемся начальным условием: N(0)=N0, откуда N0=C. Окончательно получим
(17)
т.е. численность бактерий возрастает по показательному закону.

Большое количество задач, приводящих к дифференциальным уравнениям, дает механика. Классической задачей динамики точки является задача отыскания закона движения материальной точки, если известны действующие силы. В этом случае второй закон Ньютона приводит к дифференциальному уравнению. В зависимости от действующих сил получаются уравнения самых различных типов. Рассмотрим наиболее простую из задач этого типа.

Задача4. Материальная точка массы m(г) свободно падает под действием силы тяжести. Найти закон движения точки без учёта сопротивления воздуха.
Решение. Возьмем вертикальную ось, направленную вниз, с выбранной на ней точкой отсчёта О. Положение материальной точки определяется координатой ОМ=s, изменяющейся в зависимости от времени t (Рисунок 4) Запишем второй основной закон динамики в виде
где m – масса, а - ускорение точки и F – действующая сила. По предположению, на точку действует только сила тяжести, так что
где g – ускорение силы тяжести. Ускорение а есть вторая производная от пути по времени, и мы получаем:
или
(18)

Равенство (18) представляет собой дифференциальное уравнение, содержащее вторую производную неизвестной функции s=s(t). Так как эта вторая производная оказывается здесь известной функцией от аргумента (даже просто постоянной величиной), то искомую функцию легко получить, произведя дважды интегрирование по t. Последовательно находим
(19)
(20)
Равенство (20) дает искомый закон движения, однако, как и в предыдущих задачах, оно содержит постоянные интегрирования, в данном случае – два. Их можно определить, зная начальное положение и начальную скорость точки. Пусть в начальный момент (t=0) скорость точки равна , а ее расстояние от точки отсчета О равно s0. Так как выражает скорость, то из (19) получаем , а из (20) - , и закон движения приобретает вид
Таким образом, получили известную формулу пути, пройденного точкой при равномерно ускоренном движении.

Задача5. Вычислить работу, совершаемую при сжатии пружины на 10 см, если известно (по закону Гука), что действующая сила пропорциональна сжатию пружины и что для сжатия пружины на 1 см необходима сила в 20Н.
Решение. По закону Гука сила сжатия равна F(s)=ks, где s (в метрах) – величина сжатия пружины, 0≤s≤0,1. Для нахождения коэффициента k воспользуемся тем, что по условию F(0,01)=20. Имеем: 20=k∙0,01, откуда k=2∙103 , и поэтому F(s)=2∙103s (Н), 0≤s≤0,1.
Вычислим работу по формуле
Имеем:
(Дж).

Задача6. Резервуар, наполненный водой, имеет форму цилиндра с высотой H и площадью основания S. В дне резервуара сделано отверстие площади s, через которое за 1 час вылилось 7/16 всей воды. Через сколько времени вся вода вытечет из резервуара, если скорость истечения воды выражается формулой ,где h – высота жидкости над отверстием, а k – числовой коэффициент?
Решение. Пусть через t часов после начала истечения уровень оставшейся воды равен h. За промежуток времени [t, t+∆t] уровень воды изменится на ∆h, где ∆h<0. По формуле объема цилиндра получаем, что объём вылившейся воды выражается равенством
(Рисунок5)

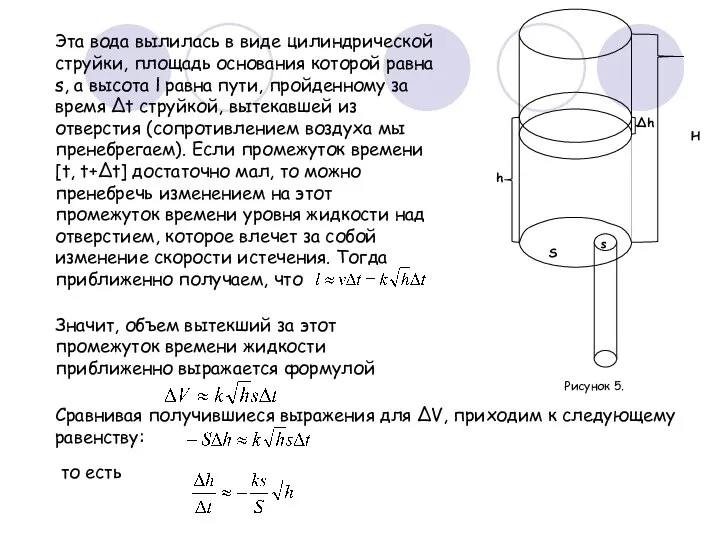
Эта вода вылилась в виде цилиндрической струйки, площадь основания которой равна s, а высота l равна пути, пройденному за время ∆t струйкой, вытекавшей из отверстия (сопротивлением воздуха мы пренебрегаем). Если промежуток времени [t, t+∆t] достаточно мал, то можно пренебречь изменением на этот промежуток времени уровня жидкости над отверстием, которое влечет за собой изменение скорости истечения. Тогда приближенно получаем, что
Значит, объем вытекший за этот промежуток времени жидкости приближенно выражается формулой
Сравнивая получившиеся выражения для ∆V, приходим к следующему равенству:
то есть

Полученное равенство становится тем более точным, чем меньше величина ∆t промежутка времени. Поэтому точным является равенство
Задача свелась к решению дифференциального уравнения (21).
Нам известно, кроме того, что в начале процесса высота воды равнялась H, а через 1 ч осталось 9/16 всей воды, и потому высота равна .
Таким образом, имеем еще условия:
и
Разделяя переменные в уравнении (21), получаем:
После интегрирования обеих частей, находим
Мы получили соотношение между моментом времени t и высотой уровня воды h. В это соотношение входят две неизвестные нам постоянные: C и
Их значения определяются из условий
и
(21)
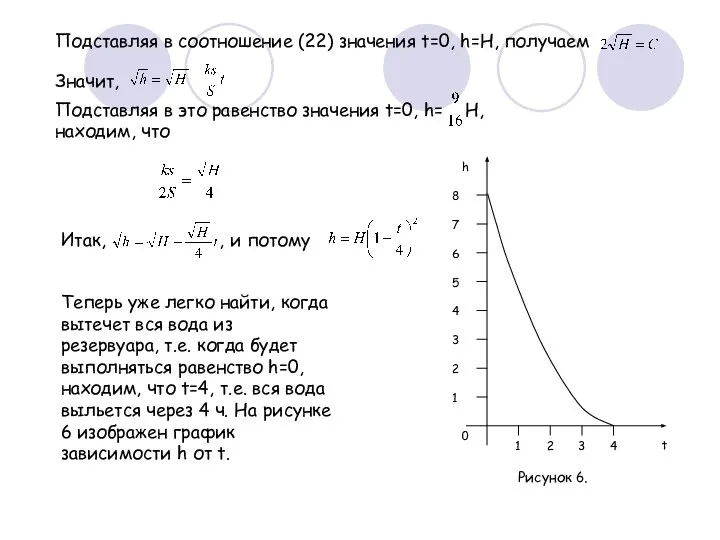
(22)

Подставляя в соотношение (22) значения t=0, h=H, получаем
Значит,
Подставляя в это равенство значения t=0, h= H,
находим, что
Итак,
, и потому
Теперь уже легко найти, когда вытечет вся вода из резервуара, т.е. когда будет выполняться равенство h=0, находим, что t=4, т.е. вся вода выльется через 4 ч. На рисунке 6 изображен график зависимости h от t.
t