Элементы комбинаторики

4. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Пример 1Из города А можно добраться в город В 3 способами, а из города В в город С 2 способами. Сколькими способами можно добраться из А в С через город В?

4. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Пример 2 Студент сдает 3 экзамена. На каждом экзамене он может получить одну из 4-х оценок. Сколько вариантов сдачи сессии существует?

4. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Пример 3 Шифр сейфа состоит из 5 цифр. Сколько комбинаций придется перебрать преступнику, вскрывающему сейф?

4. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Пример 4. 5 человек выстраиваются в очередь. Сколько способов выстроиться в очередь существует?

4. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Пример 5. Сколько существует способов упорядочить n элементов множества?

4. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Число перестановок n-элементного множества равно

4. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Пример 6 Шифр сейфа состоит из 5 цифр. Сколько комбинаций придется перебрать преступнику, вскрывающему сейф, если он знает, что все цифры в шифре разные?

4. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Пример 7 Множество включает n элементов. Сколько способов выбрать из этого множества m элементов, если порядок элементов важен?

число размещений
из n элементов по m
Размещениями из n элементов по m называются
упорядоченные наборы в m элементов, взятых
из множества, состоящего из n элементов.

Пример 8. Из группы в 5 человек надо выбрать троих на конференцию. Сколькими способами это можно сделать?

число сочетаний
из n элементов по m
Сочетаниями из n элементов по m называются
неупорядоченные наборы в m элементов, взятых
из множества, состоящего из n элементов.

Пример 9. Студенту предлагается выбрать из 6 спецкурсов два, который он должен изучить в семестре. Сколькими способами он может это сделать?

Брошено три игральные кости. Найти вероятности событий: A – на всех костях выпало одинаковое число очков
В – на всех костях выпало разное число очков.
Пример.

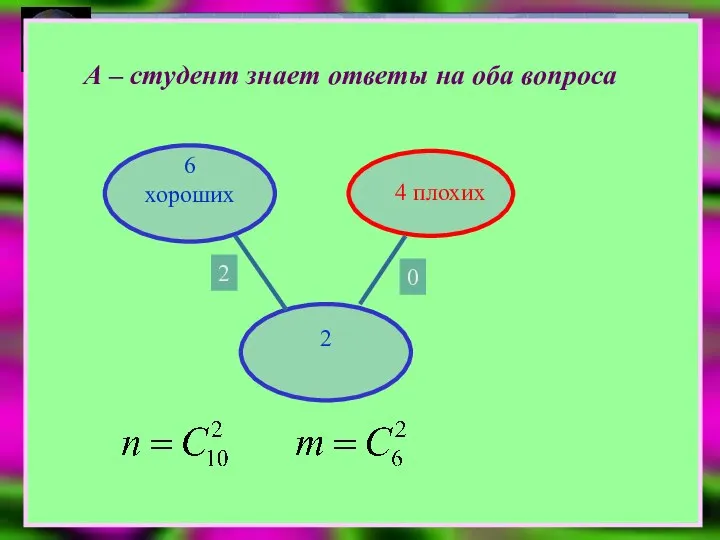
На экзамене может быть предложено 10 вопросов. Студент знает ответы на 6 из них. Преподаватель выбирает наудачу 2 вопроса.
Найти вероятности событий:
А – студент знает ответы на оба вопроса
В – студент знает ответы на 1 вопрос
С – студент не знает ответа на оба вопроса.
Пример.

А – студент знает ответы на оба вопроса
6 хороших
4 плохих
2
2
0

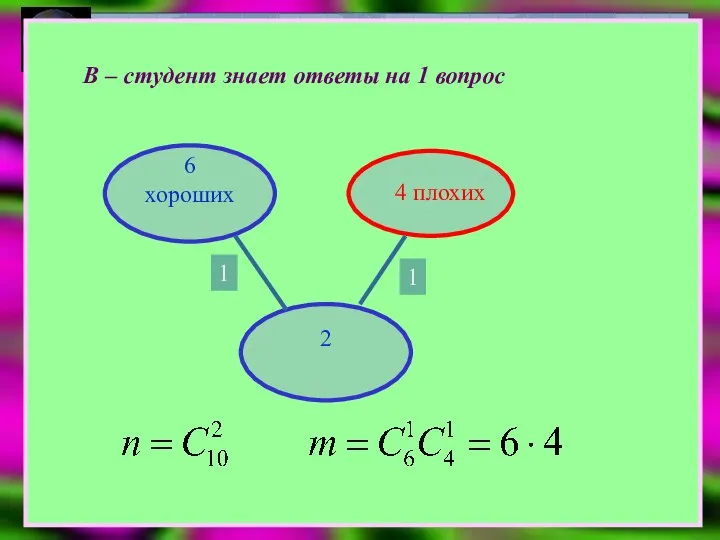
В – студент знает ответы на 1 вопрос
6 хороших
4 плохих
2
1
1