Содержание
- 2. ДНФ и импликанты Функция f имплицирует функцию g, если . Замечание: Если , то .
- 3. Импликант Если f имплицирует g, и f представлена единственной элементарной конъюнкцией, то f называется импликантом g.
- 4. Если функция представима единственной элементарной конъюнкцией – всех n переменных, то ; – m . Теорема
- 5. Пусть . Она принимает значение 1 тогда и только тогда, когда x = 1, y =
- 6. Пример Пусть . Она принимает значение 1 тогда и только тогда, когда y = 0, z
- 7. Утверждение 1 Представление функции в виде ДНФ соответствует представлению ее единичного множества в виде объединения единичных
- 8. Пример Пусть функция представлена своей ДНФ. . Тогда ее единичное множество может быть представлено в виде:
- 9. Утверждение 2 Любая конъюнкция ДНФ функции является импликантом данной функции.
- 10. Утверждение 3 Если конъюнкция ДНФ функции не является простым импликантом, то можно найти соответствующий ей простой
- 11. Определение ДНФ, состоящая только из простых импликантов, называется сокращенной. .
- 12. Пример Пусть функция представлена своей ДНФ. Тогда ее единичное множество имеет вид:
- 13. Пример Очевидно, что – это простой импликант. Он состоит из одной буквы, и если ее вычеркнуть,
- 14. Пример Проверим, будет ли простым импликант . Вычеркнем из него переменную х.
- 16. Скачать презентацию













 Решение задач
Решение задач 8c3f0c24-2702-4093-8e3e-0619d16772a5
8c3f0c24-2702-4093-8e3e-0619d16772a5 Вписанная и описанная окружности
Вписанная и описанная окружности Описание линейной дискретной системы в частотной области (ЛДС). Частотные характеристики ЛДС
Описание линейной дискретной системы в частотной области (ЛДС). Частотные характеристики ЛДС Действия с числами, записанными в стандартном виде
Действия с числами, записанными в стандартном виде Избранные вопросы и задачи планиметрии. Пособие для факультативных занятий
Избранные вопросы и задачи планиметрии. Пособие для факультативных занятий Обобщение и систематизация знаний и умений решения линейных уравнений с одной переменной в 7 классе
Обобщение и систематизация знаний и умений решения линейных уравнений с одной переменной в 7 классе Великолепная пятерка. Математический калейдоскоп
Великолепная пятерка. Математический калейдоскоп Задачи с кубиками
Задачи с кубиками Построения в пространстве
Построения в пространстве Последовательности. Золотое сечение
Последовательности. Золотое сечение Презентация на тему Показательная функция и ее свойства
Презентация на тему Показательная функция и ее свойства  Тела вращения. Цилиндр
Тела вращения. Цилиндр Метод наименьших квадратов
Метод наименьших квадратов Відстань між двома точками. Координати середини відрізка
Відстань між двома точками. Координати середини відрізка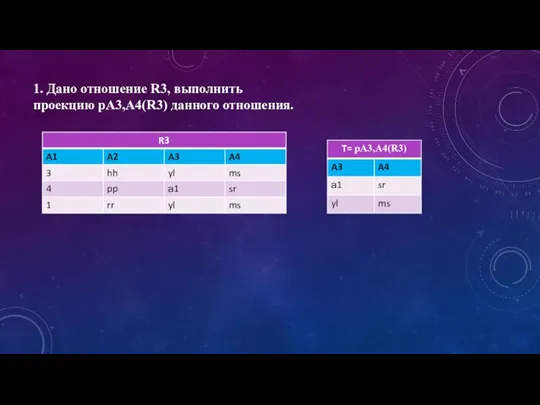 Дано отношение R3, выполнить проекцию pA3,A4(R3) данного отношения
Дано отношение R3, выполнить проекцию pA3,A4(R3) данного отношения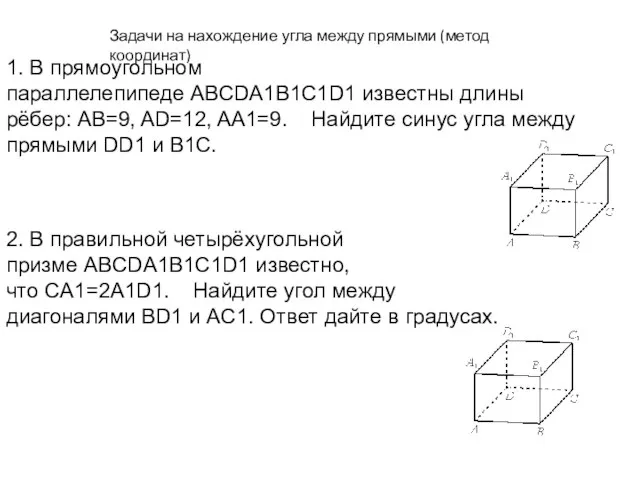 Задачи на нахождение угла между прямыми (метод координат)
Задачи на нахождение угла между прямыми (метод координат) Упростите выражение
Упростите выражение Логика высказываний и булевы алгебры (Boolean Algebra and Logic)
Логика высказываний и булевы алгебры (Boolean Algebra and Logic) Игра марафон - посчитай предметы
Игра марафон - посчитай предметы Правильные многогранники
Правильные многогранники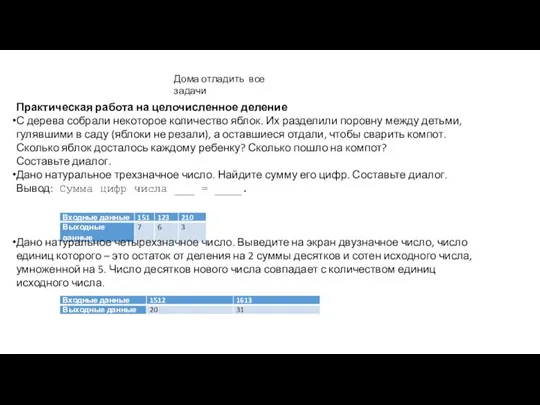 Практическая работа на целочисленное деление
Практическая работа на целочисленное деление График функции. Урок применения знаний и умений. Класс: 8
График функции. Урок применения знаний и умений. Класс: 8 Комбинации многогранников и тел вращения
Комбинации многогранников и тел вращения Математика в литературе
Математика в литературе Таблицы. Геометрия
Таблицы. Геометрия Нечеткие дифференциальные уравнения
Нечеткие дифференциальные уравнения Понятие логарифма
Понятие логарифма