Первообразная

«Будущее за профессиями, способными работать в информационном обществе.»
А.Ф. Киселев
Основные вопросы урока:
Понятие интегрирования.
Определение первообразной.
Примеры нахождения первообразных.
Основное свойство первообразной.
Геометрический смысл основного свойства первообразной.
Таблица первообразных.

Дифференцирование
Интегрирование
Понятие интегрирования
Интегрирование – операция, обратная дифференцированию

Найти функцию F, если известно, что
Вместо точек поставьте какую – нибудь функцию, удовлетворяющую равенству:
Определение первообразной
Определение. Функция F называется первообразной для функции f на заданном промежутке, если для всех x из этого промежутка
Устные упражнения

Примеры нахождения первообразной
Пример 1. Функция есть первообразная для
функции на интервале , т.к.
Пример 2. Тело движется по закону
Доказать, что скорость определяется формулой
Доказательство

Основное свойство первообразной
Все первообразные функции можно записать с помощью одной формулы, которую называют общим видом первообразных для функции . Справедлива следующая теорема (основное свойство первообразных):
Теорема Любая первообразная для функции на промежутке может быть записана в виде
(1)
Где - одна из первообразных для функции на промежутке , а - произвольная постоянная.

Доказательство
По условию функция – первообразная
для на промежутке . Следовательно,
для любого , поэтому –
- первообразная для функции .

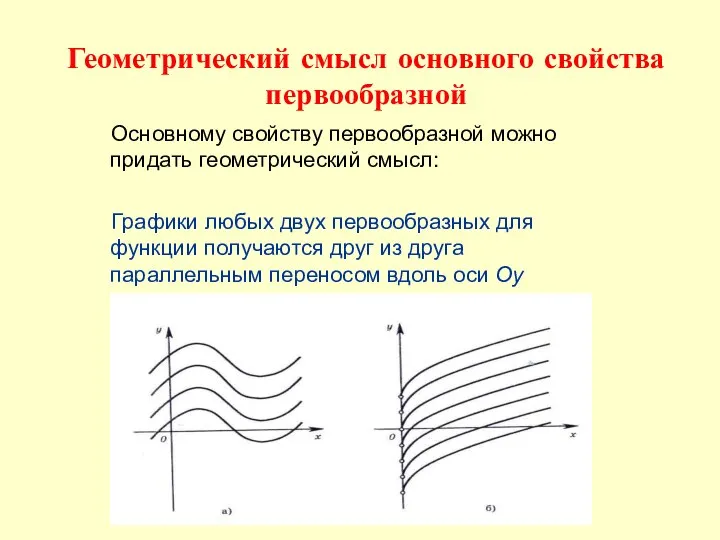
Геометрический смысл основного свойства первообразной
Основному свойству первообразной можно придать геометрический смысл:
Графики любых двух первообразных для функции получаются друг из друга параллельным переносом вдоль оси Оу