Содержание
- 2. Дифференциальные уравнения. Основные понятия и определения. Виды дифференциальных уравнений. Дифференциальные уравнения 1-го порядка. Основные вопросы:
- 3. Мудрецы говорили, что законы нашей вселенной написаны на математическом языке. Конечно, в алгебре есть много примеров
- 4. ОПРЕДЕЛЕНИЕ Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функции и производные (или дифференциалы) этой функции.
- 5. Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные)
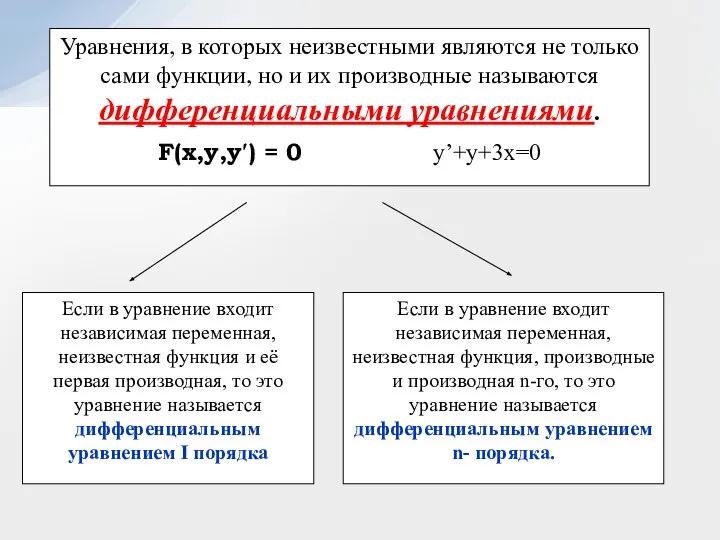
- 6. Уравнения, в которых неизвестными являются не только сами функции, но и их производные называются дифференциальными уравнениями.
- 7. Наивысший порядок производных, входящих в уравнение, называется порядком дифференциального уравнения ОПРЕДЕЛЕНИЕ
- 8. Общим решением дифференциального уравнения называется такая дифференцируемая функция y = ϕ(x, C), которая при подстановке в
- 9. Задачей Коши (Огюстен Луи Коши (1789-1857)- французский математик) называется нахождение любого частного решения дифференциального уравнения вида
- 10. Найти общее решение дифференциального уравнения. Подставить в полученную функцию начальные значения x и y, и найти
- 11. ПРИМЕР. Найти общее и частное решение дифференциального уравнения РЕШЕНИЕ: Общее решение дифференциального уравнения ищется с помощью
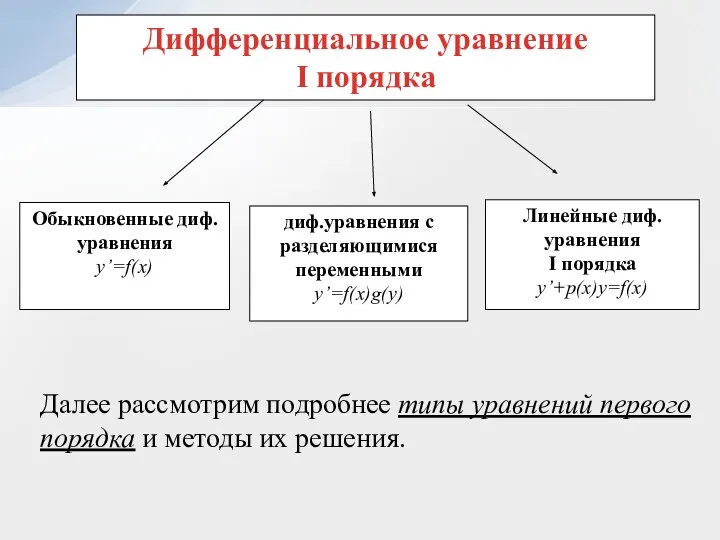
- 13. Дифференциальным уравнением 1-го порядка называется соотношение, связывающее функцию, ее первую производную и независимую переменную, т.е. соотношение
- 14. Дифференциальное уравнение I порядка Обыкновенные диф.уравнения y’=f(x) диф.уравнения с разделяющимися переменными y’=f(x)g(y) Линейные диф.уравнения I порядка
- 15. Уравнение вида называется дифференциальным уравнение 1-го порядка с разделенными переменными. ОПРЕДЕЛЕНИЕ
- 16. ПРИМЕР.
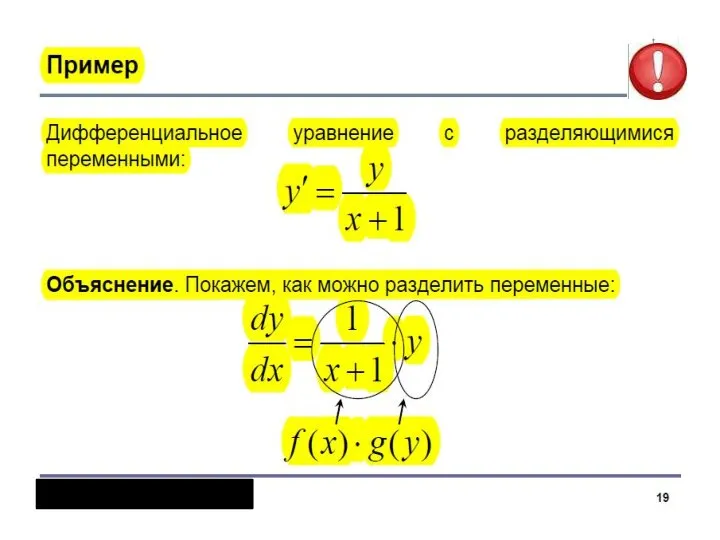
- 17. Дифференциальное уравнение y’=f(x)g(y) называется уравнением с разделяющимися переменными, если его можно записать в виде ОПРЕДЕЛЕНИЕ
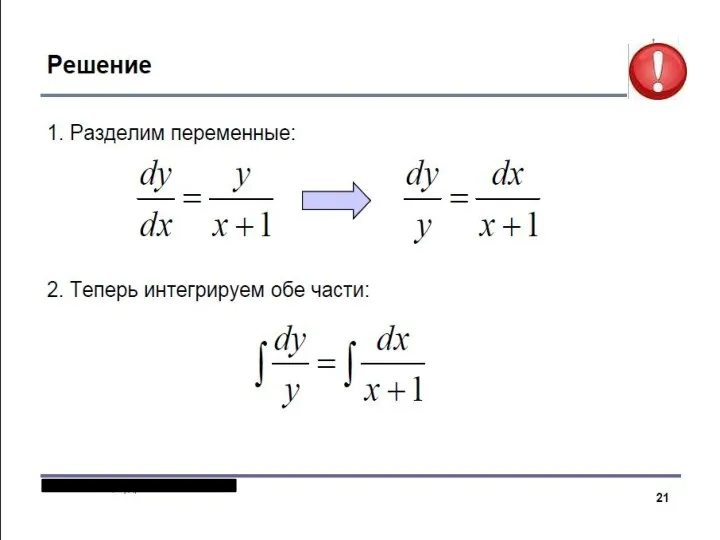
- 18. Эти уравнения легко сводятся к уравнению с разделёнными переменными. Записываем уравнение в форме: затем делим на
- 19. Пример: Выразим у из последнего выражения как функцию х, получим общее решение:
- 25. Применение дифференциальных уравнений для решения задач
- 26. Закон растворения лекарственных форм вещества из таблеток Скорость растворения лекарственных форм вещества из таблеток пропорциональна количеству
- 27. Закон размножения бактерий с течением времени Скорость размножения некоторых бактерий пропорциональна количеству бактерий в данный момент.
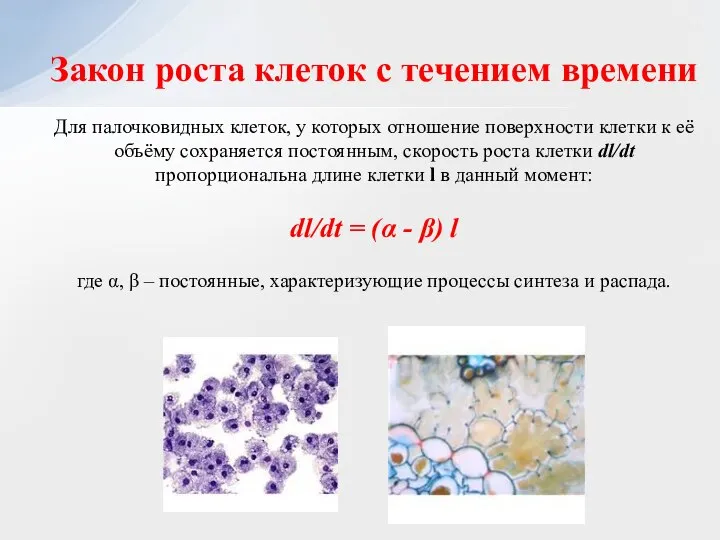
- 28. Закон роста клеток с течением времени Для палочковидных клеток, у которых отношение поверхности клетки к её
- 29. Закон разрушения клеток в звуковом поле Кавитация ультразвуковых волн проявляется в виде разрывов суспензионной среды и
- 30. Внутривенное введение глюкозы При внутривенном введении глюкозы с помощью капельницы скорость поступления глюкозы в кровь постоянна
- 31. Теория эпидемий В теории эпидемий при условии, что изучаемое заболевание носит длительный характер, процесс передачи инфекции
- 32. Теория эпидемий При этих условиях нужно установить закон изменения числа незаражённых особей с течением времени, т.е.
- 33. Пример: Составьте дифференциальное уравнение и найдите частные решения. Концентрация лекарственного препарата в крови уменьшается вследствие выведения
- 34. Решение: Решая полученное уравнение, получаем: где m0-концентрация вещества в крови в начальный момент времени t=0, m
- 35. Решение: Потенцируя, получим: По условию задачи m0=0,2 мг/л, m=m0/2 мг/л, t=23 ч. Подставляем и находим: Зависимость
- 36. Домашнее задание: Колесов В.В. Математика для медицинских колледжей: учебное пособие/В.В.Колесов, М.Н. Романов. – Ростов н/Д: Феникс,
- 38. Скачать презентацию






























 Цепочка бусин
Цепочка бусин Аксиомы и теоремы
Аксиомы и теоремы Решение уравнений. Устная работа
Решение уравнений. Устная работа ОДУ высших порядков
ОДУ высших порядков Экстремум функции нескольких переменных. Наибольшее и наименьшее значение функции в замкнутой ограниченной области (тема 1.4)
Экстремум функции нескольких переменных. Наибольшее и наименьшее значение функции в замкнутой ограниченной области (тема 1.4) Презентация на тему Решение неравенств второй степени с одной переменной
Презентация на тему Решение неравенств второй степени с одной переменной  Прогрессии. Основные формулы арифметической прогрессии
Прогрессии. Основные формулы арифметической прогрессии Презентация на тему Цифра 5, число 5, состав числа 5
Презентация на тему Цифра 5, число 5, состав числа 5  Интегрированный урок математики и краеведения. Путешествие по Кизильскому району. Часть 1
Интегрированный урок математики и краеведения. Путешествие по Кизильскому району. Часть 1 Вставляем пропущенное число с дракончиками. Урок математики
Вставляем пропущенное число с дракончиками. Урок математики Задачи на построение
Задачи на построение Аттестационная работа. Доли. Обыкновенные дроби. (5 класс)
Аттестационная работа. Доли. Обыкновенные дроби. (5 класс) Следствия из теорем синусов и косинусов
Следствия из теорем синусов и косинусов Примеры на состав числа 6
Примеры на состав числа 6 Найдите лишнюю фигуру и объясните свой выбор
Найдите лишнюю фигуру и объясните свой выбор Объем тела. Объем призмы, пирамиды, усечённой пирамиды
Объем тела. Объем призмы, пирамиды, усечённой пирамиды Математическая игра «Звездный час»
Математическая игра «Звездный час» Множення і ділення
Множення і ділення Диференціальне числення функції однієї змінної
Диференціальне числення функції однієї змінної Декартова система координат в пространстве
Декартова система координат в пространстве П 3
П 3 Математическая тревожность
Математическая тревожность Презентация на тему Транспортир. Измерение углов транспортиром
Презентация на тему Транспортир. Измерение углов транспортиром  Линейная алгебра. Матрицы
Линейная алгебра. Матрицы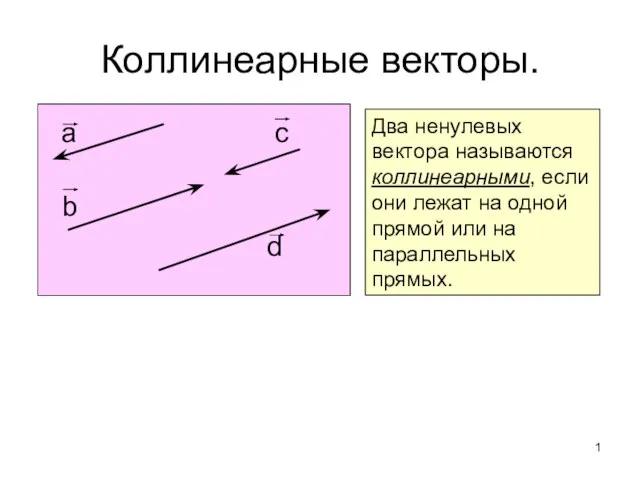 Коллинеарные векторы
Коллинеарные векторы Задачи на количество
Задачи на количество Урок 14. Первый признак равенства треугольников
Урок 14. Первый признак равенства треугольников Таблица умножения в пределах 100. Урок повторения и закрепления
Таблица умножения в пределах 100. Урок повторения и закрепления