Содержание
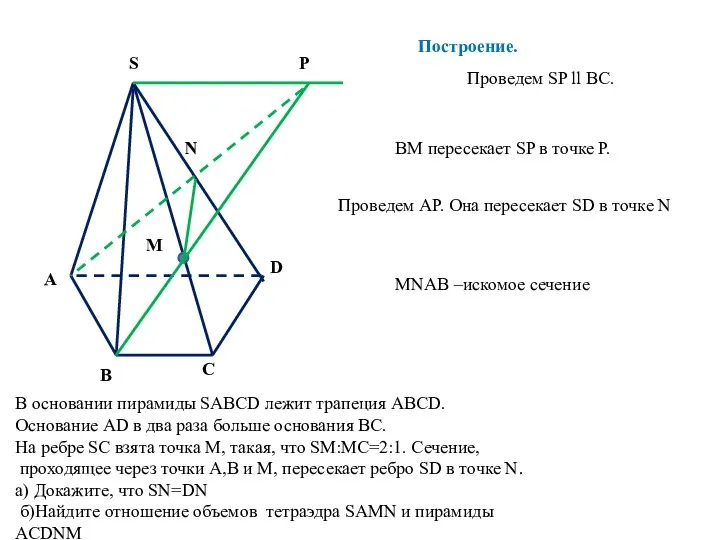
- 2. Вариант 201 В основании пирамиды SABCD лежит трапеция ABCD. Основание AD в два раза больше основания
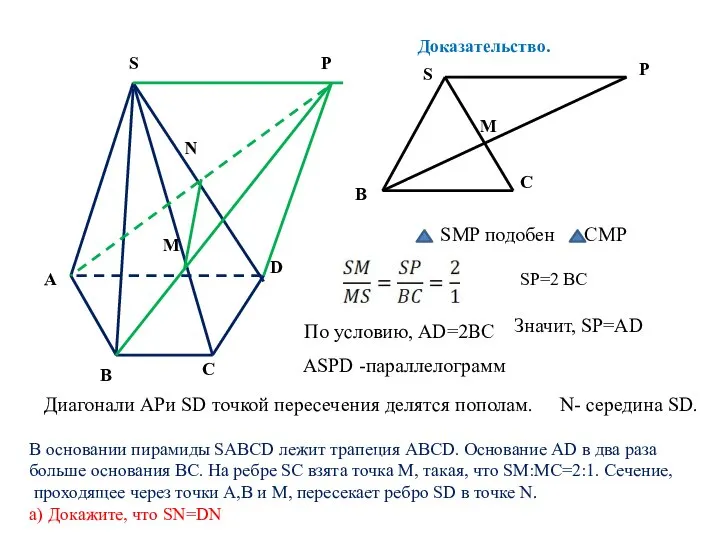
- 3. S A D B C В основании пирамиды SABCD лежит трапеция ABCD. Основание AD в два
- 4. S A D B C В основании пирамиды SABCD лежит трапеция ABCD. Основание AD в два
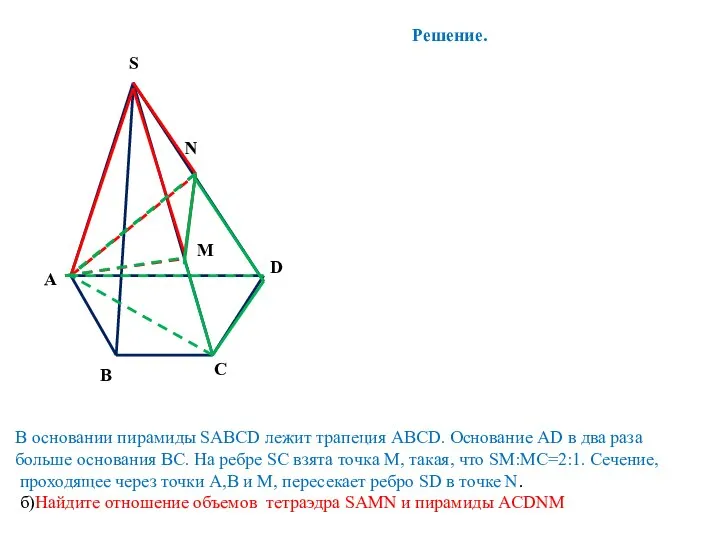
- 5. S A D B C В основании пирамиды SABCD лежит трапеция ABCD. Основание AD в два
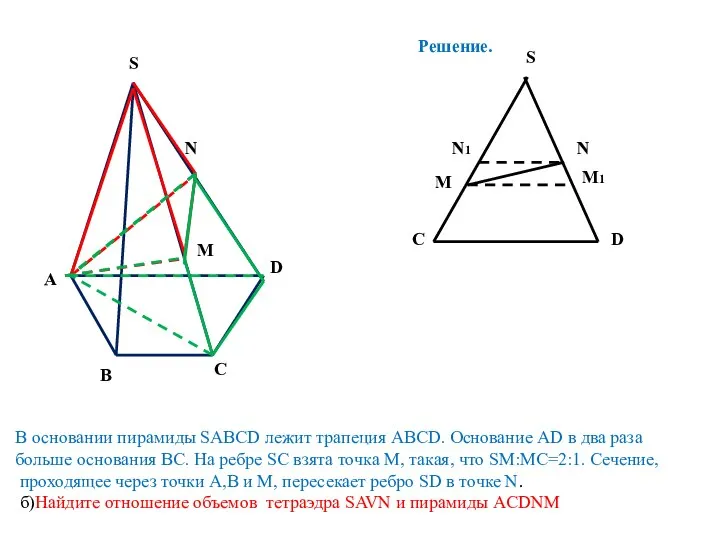
- 6. S A D B C В основании пирамиды SABCD лежит трапеция ABCD. Основание AD в два
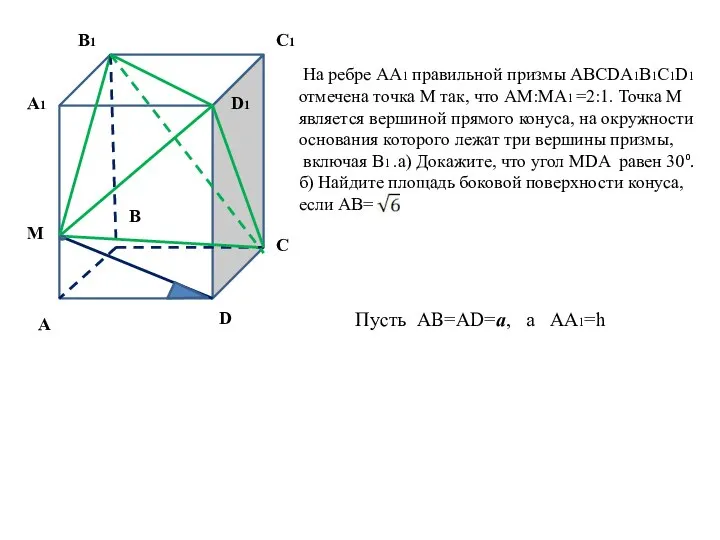
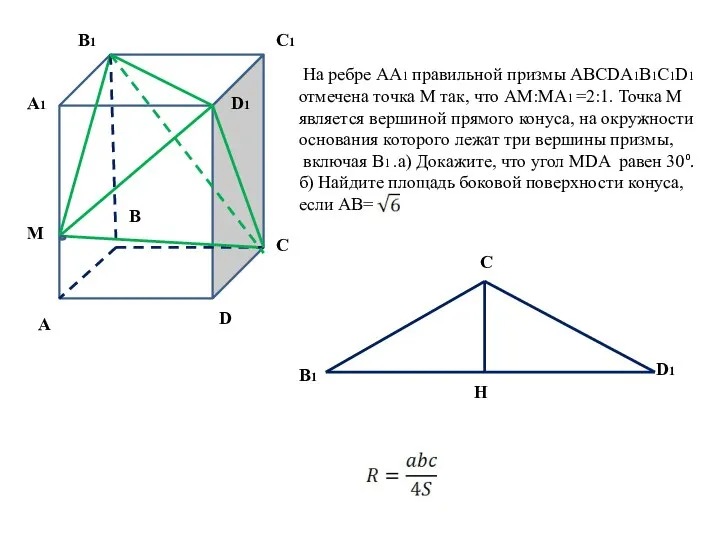
- 7. Вариант 203 На ребре А 1 правильной призмы ABCDA1B1C1D1 отмечена точка М так, что АМ:МА1 =2:1.
- 8. M D1 С С1 D В1 А1 А В На ребре АА1 правильной призмы ABCDA1B1C1D1 отмечена
- 9. M D1 С С1 D В1 А1 А В На ребре АА1 правильной призмы ABCDA1B1C1D1 отмечена
- 11. Скачать презентацию


 قدرمطلقی درجه اول
قدرمطلقی درجه اول Способы решения показательных уравнений
Способы решения показательных уравнений Преобразования графиков
Преобразования графиков Математика. 3 класс
Математика. 3 класс Презентация на тему Страна отрицательных чисел
Презентация на тему Страна отрицательных чисел  Презентация на тему Угол вписанный в окружность
Презентация на тему Угол вписанный в окружность  Великолепная пятерка. Математический калейдоскоп
Великолепная пятерка. Математический калейдоскоп Обобщающий урок по начертательной геометрии прямая. Плоскость
Обобщающий урок по начертательной геометрии прямая. Плоскость Раскрытие скобок
Раскрытие скобок Планиметрия. Четырёхугольники
Планиметрия. Четырёхугольники Решение по готовы чертежам по теме: Длина окружности, 9 класс
Решение по готовы чертежам по теме: Длина окружности, 9 класс Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями Матричный способ решения СЛАУ и метод Крамера
Матричный способ решения СЛАУ и метод Крамера Рациональные приемы вычислений
Рациональные приемы вычислений Подготовка к ВПР. Равенство
Подготовка к ВПР. Равенство pril1
pril1 Шкала. Координатный луч
Шкала. Координатный луч Степенные ряды
Степенные ряды Числовые промежутки
Числовые промежутки Prezentado de enspezoj
Prezentado de enspezoj Сравнение чисел. 1 класс
Сравнение чисел. 1 класс Раскрытие скобок
Раскрытие скобок Математика 1 класс. УМК Перспектива. Урок 1. Форма предметов
Математика 1 класс. УМК Перспектива. Урок 1. Форма предметов Построение информационной модели метода изготовления изделия
Построение информационной модели метода изготовления изделия Геометрические построения
Геометрические построения Числовая окружность на координатной плоскости
Числовая окружность на координатной плоскости ЕГЭ 2021. Задания 1-19 (11 класс)
ЕГЭ 2021. Задания 1-19 (11 класс) Метрология
Метрология