Пифагор и его школа

Пифагор Самосский
Великий древнегреческий ученый Пифагор родился на острове Самос в VI в. до н.э. В молодости побывал в Египте, где учился у жрецов. Говорят, что он был допущен в сокровенные святилища Египта, посетил халдейских мудрецов и персидских магов.

Школа Пифагора
Около 530 г. До н. э. Пифагор переехал в Кротон – греческую колонию в Южной Италии, где основал так называемый пифагорейский союз (или кротонское братство). В сферу интересов членов союза входили научные исследования, религиозно-философские искания, политическая деятельность.

Школа Пифагора
Они вели суровый образ жизни, превыше всего ценили самообладание, смелость и коллективную дисциплину. Пифагорейцы жили вместе, у них было совместное имущество, и даже свои открытия они считали общим достоянием.

Школа Пифагора
Деятельность союза была окружена тайной, поэтому никаких текстов от ранних пифагорейцев не осталось. Кроме того, по традиции, они все открытия приписывали Пифагору, о котором уже при жизни ходили легенды. Кто на самом деле является автором того или иного результата, неизвестно.

Школа Пифагора
Пифагорейцы называли собственные исследования «математа», что означает «науки», и делили их на четыре части: арифметику, геометрию, астрономию и гармонию (учение о музыке).

Арифметика

Пифагорейцы представляли числа как совокупности точек, образующих геометрические конфигурации – наподобие рисунка из камешков на земле. Таким образом, под числом они подразумевали «множество единиц» (греч. «аритмос») и признавали только целые положительные (т. е. натуральные) числа, разделяя их на чётные и нечётные.
Представление чисел

(Позже Платон говорил, что арифметика есть учение о чётном и нечётном.)
Пифагорейцы доказали первую теорему теории делимости: произведение двух чисел чётно тогда и только тогда, когда чётно по крайней мере одно из них.

Они поставили также задачу о нахождении совершенных чисел, т. е. чисел, равных сумме своих делителей (см. статью «Совершенные и дружественные числа»). Единица считалась неделимой, у неё не было «долей».

Вместо этого пифагорейцы рассматривали отношения (т. е. пропорции) целых чисел. К примеру, они могли сказать, что 2 точно так относится к 3, как 4 к 6. Говоря современным языком, они построили теорию рациональных чисел как теорию пар.

Её изложение дошло до нас в «Началах» Евклида (III в. до н. э.).

ГЕОМЕТРИЯ

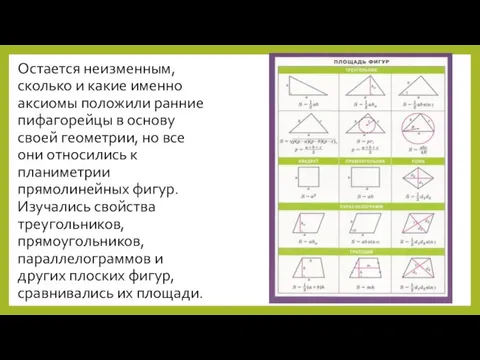
Остается неизменным, сколько и какие именно аксиомы положили ранние пифагорейцы в основу своей геометрии, но все они относились к планиметрии прямолинейных фигур. Изучались свойства треугольников, прямоугольников, параллелограммов и других плоских фигур, сравнивались их площади.

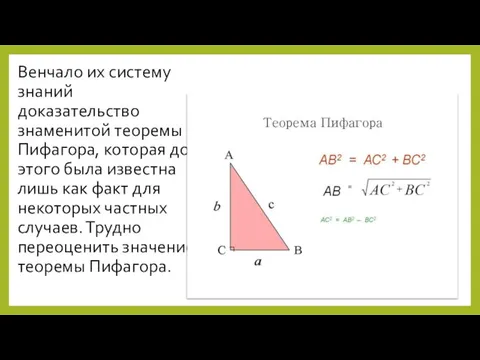
Венчало их систему знаний доказательство знаменитой теоремы Пифагора, которая до этого была известна лишь как факт для некоторых частных случаев. Трудно переоценить значение теоремы Пифагора.

Ее обобщение и сегодня лежит в основе определения всех метрических пространств. Можно утверждать, что и в стереометрии пифагорейцы достигли значительных успехов. По свидетельству греческого историка и философа V в. Прокла, именно они построили пять правильных многогранников:

Тетраэдр, куб, октаэдр, додекаэдр, икосаэдр. Правда, многие современные исследователи считают, что Пифагору были известны лишь куб, тетраэдр и додекаэдр, а октаэдр и икосаэдр открыл Теэтет Афинский ( IV в. До н. э. ), талантливый ученик пифагорейца Феодора Киренского и Платона.

Астрономия и гармония

Пифагорейцы считали, что земля имеет форму шара и находится в центре Вселенной: ведь нет никаких оснований, чтобы она была смещена или вытянута в какую-то одну сторону. Солнце же, Луна и пять планет ( Меркурий, Венера, Марс, Юпитер и Сатурн ) движутся вокруг Земли.

Расстояния от них до нашей планеты таковы, что они как бы составляют семиструнную арфу, и при их движении возникает прекрасная музыка – музыка сфер. Обычно люди не слышат ее из-за суеты жизни, и лишь после смерти некоторые из них смогут насладиться ею. А Пифагор слышал ее и при жизни.

Строй арфы должен был подчиняться законам арифметики. В частности, как обнаружили пифагорейцы, такие музыкальные интервалы, как октава, квинта и кварта, соответствуют звучанию пары одинаково натянутых струн, длины которых находятся в отношении 1:2, 2:3, и 3:4. Все эти открытия и привели пифагорейцев к идее о том, что « все есть число», т.е. законы природы – не что иное, как законы целых чисел и их отношений.

Открытие иррациональности

Вначале пифагорейцы полагали, что отношения любых физических или геометрических величин можно выразить отношениями целых чисел. В частности, они считали, что все отрезки соизмеримы, т.е. каковы бы ни были два отрезка AB и CD, существует такой отрезок e, который целое число раз укладывается как по длине AD, так и по длине CD, а значит, геометрию можно свести к арифметике.

Однако вскоре пифагорейцы сделали открытие, которое перевернуло все их взгляды они доказали, что отношение диагонали к стороне квадрата нельзя выразить отношением чисел.

Позже были найдены и другие несоизмеримые отрезки. В частности, Феодор Киренсон обнаружил, что стороны квадратов с площадями 3, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15 несоизмеримые со стороной единичного квадрата. А Теодор доказал,что если площадь квадрата выражается любым целым неквадратным числом N,то сторона его несоизмерима с единицей.