Презентация на тему Построение сечений: метод следа

Существует три основных метода построения сечений многогранников:
Метод следов.
Метод вспомогательных сечений.
Комбинированный метод.

Метод следов заключается в построении следов секущей плоскости на плоскость каждой грани многогранника.
Построение сечения многогранника методом следов обычно начинают с построения так называемого основного следа секущей плоскости, т.е. следа секущей плоскости на плоскости основания многогранника.

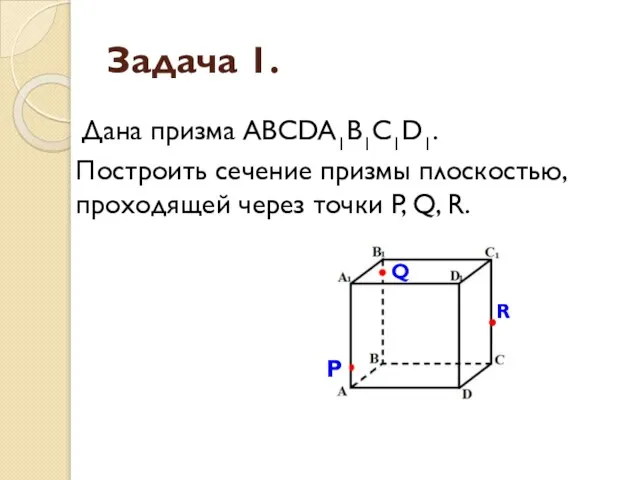
Задача 1.
Дана призма ABCDA1B1C1D1.
Построить сечение призмы плоскостью, проходящей через точки P, Q, R.
P
Q
R

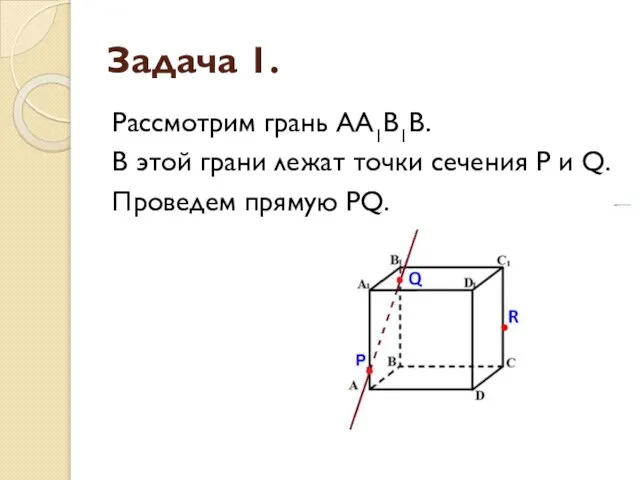
Задача 1.
Рассмотрим грань АА1В1В.
В этой грани лежат точки сечения P и Q.
Проведем прямую PQ.

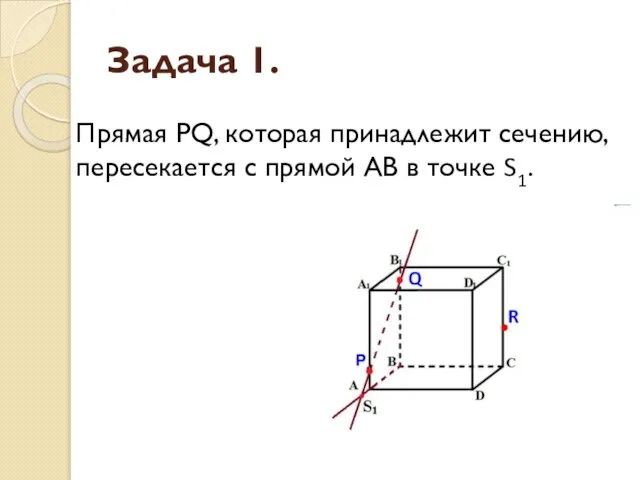
Задача 1.
Прямая PQ, которая принадлежит сечению, пересекается с прямой АВ в точке S1.

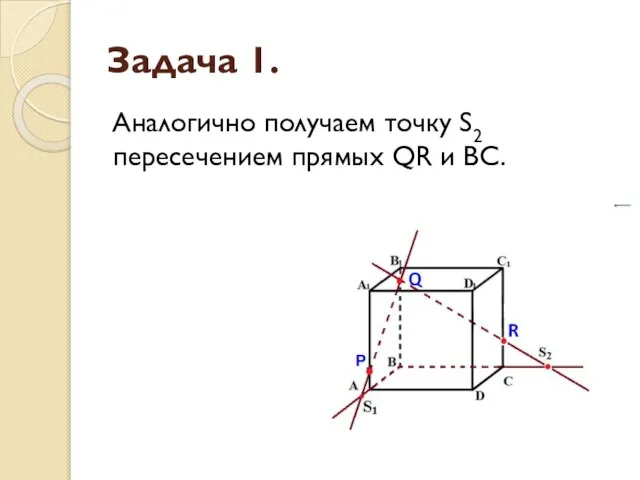
Задача 1.
Аналогично получаем точку S2 пересечением прямых QR и BC.

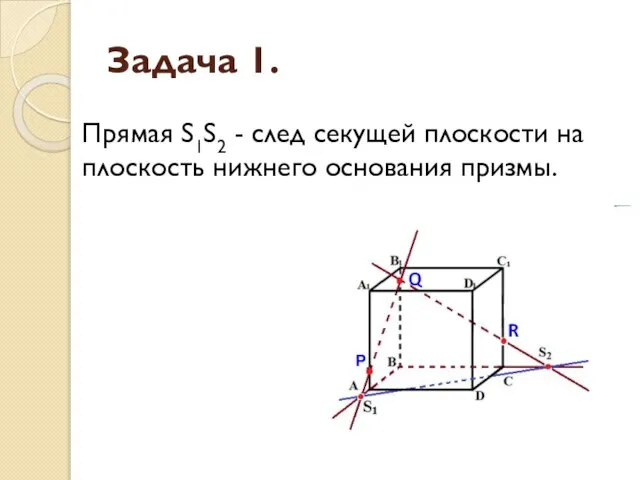
Задача 1.
Прямая S1S2 - след секущей плоскости на плоскость нижнего основания призмы.

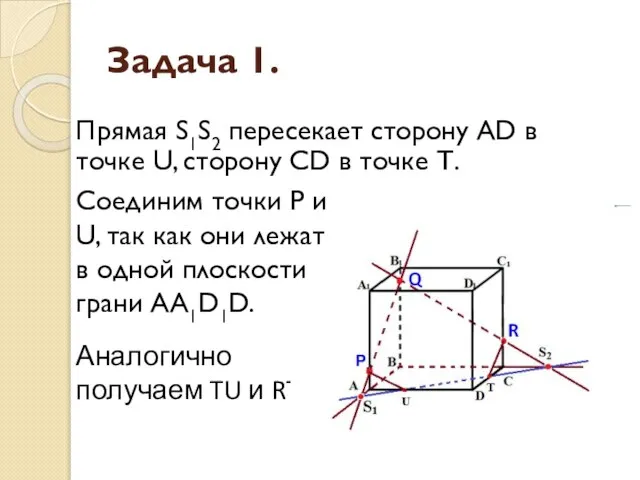
Задача 1.
Прямая S1S2 пересекает сторону AD в точке U, сторону CD в точке Т.
Аналогично получаем TU и RT.
Соединим точки P и U, так как они лежат в одной плоскости
грани АА1D1D.

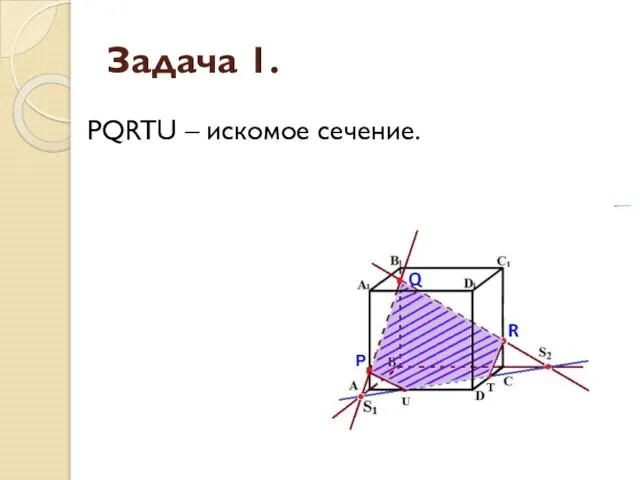
Задача 1.
PQRTU – искомое сечение.

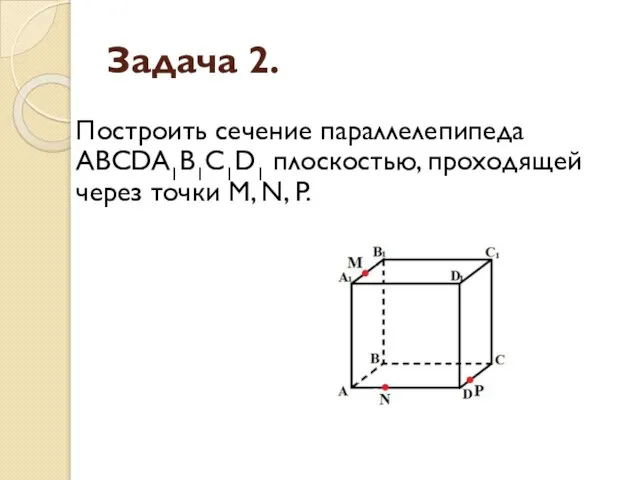
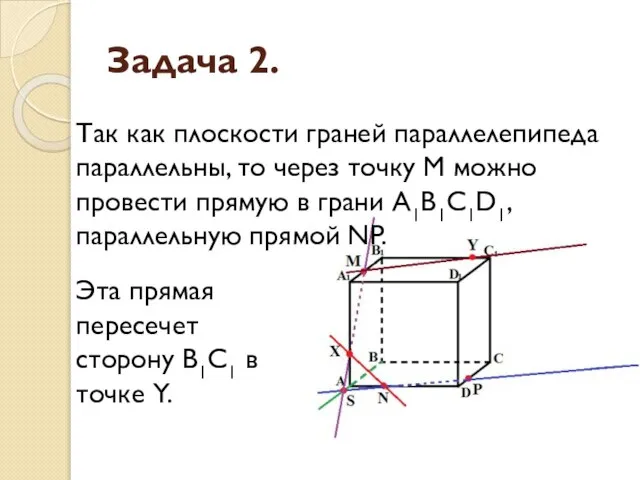
Задача 2.
Построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через точки M, N, P.

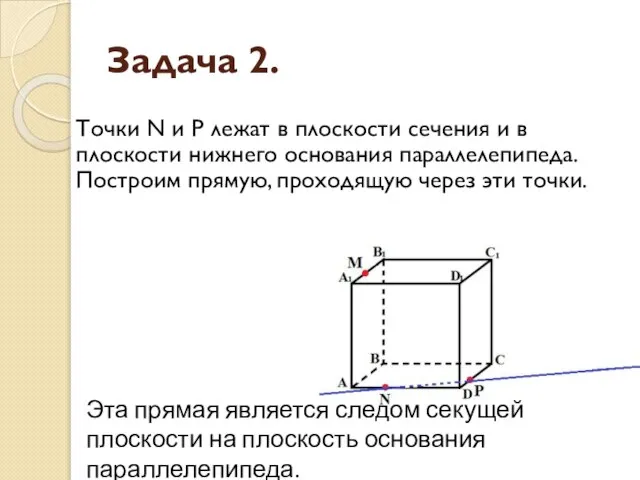
Задача 2.
Точки N и P лежат в плоскости сечения и в плоскости нижнего основания параллелепипеда. Построим прямую, проходящую через эти точки.
Эта прямая является следом секущей плоскости на плоскость основания параллелепипеда.

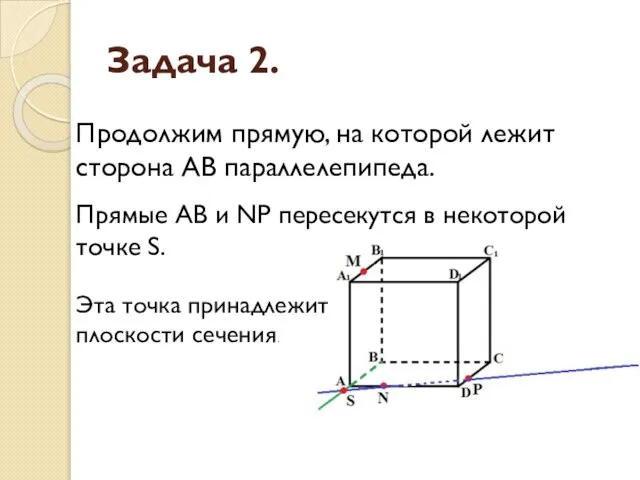
Задача 2.
Продолжим прямую, на которой лежит сторона AB параллелепипеда.
Прямые AB и NP пересекутся в некоторой точке S.
Эта точка принадлежит плоскости сечения.

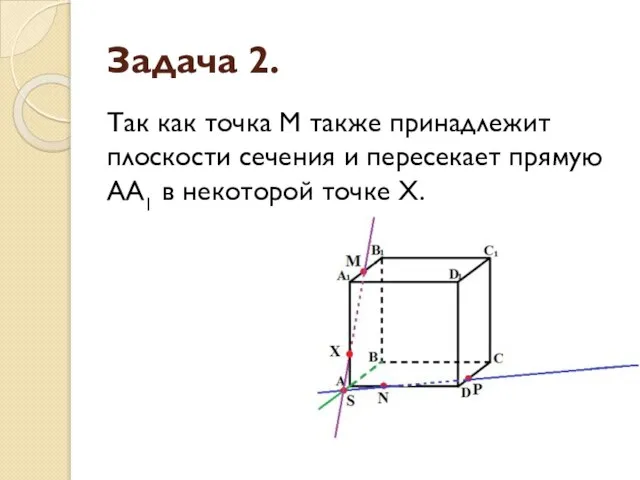
Задача 2.
Так как точка M также принадлежит плоскости сечения и пересекает прямую АА1 в некоторой точке Х.

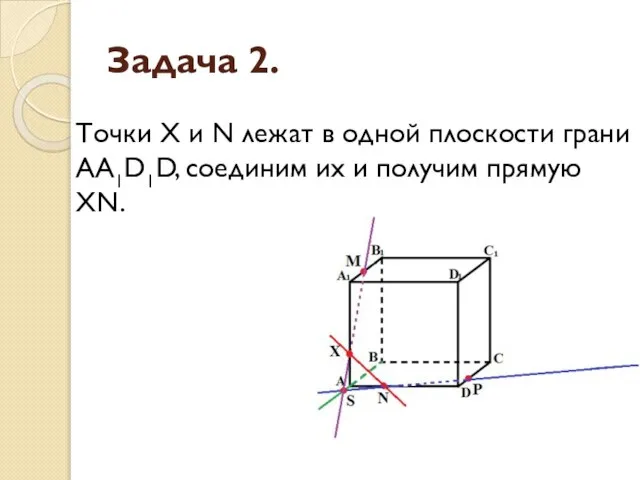
Задача 2.
Точки X и N лежат в одной плоскости грани АА1D1D, соединим их и получим прямую XN.

Задача 2.
Эта прямая пересечет сторону В1С1 в точке Y.
Так как плоскости граней параллелепипеда параллельны, то через точку M можно провести прямую в грани A1B1C1D1, параллельную прямой NP.

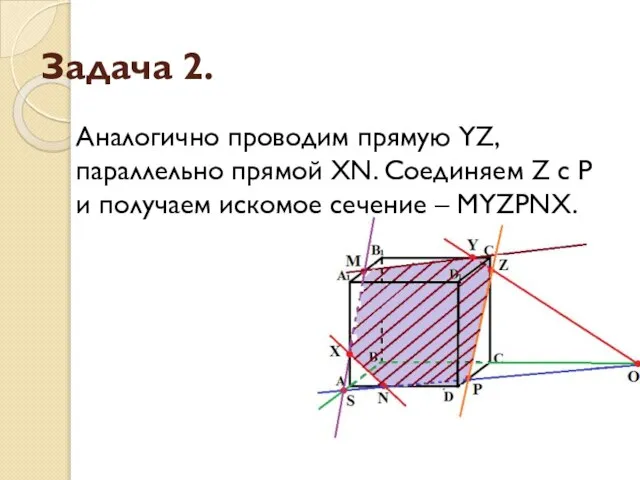
Задача 2.
Аналогично проводим прямую YZ, параллельно прямой XN. Соединяем Z с P и получаем искомое сечение – MYZPNX.

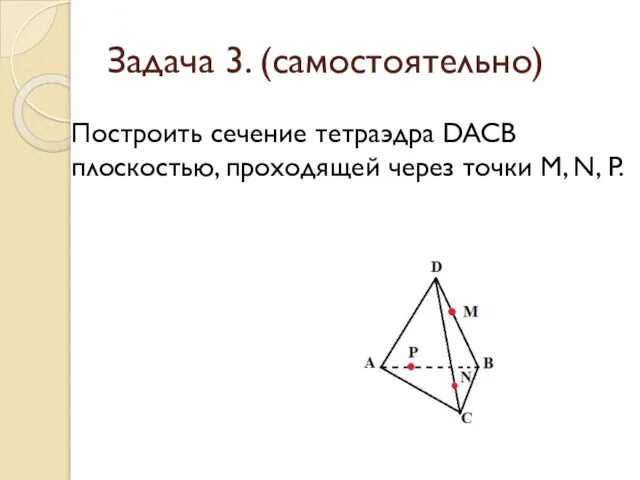
Задача 3. (самостоятельно)
Построить сечение тетраэдра DACB плоскостью, проходящей через точки M, N, P.

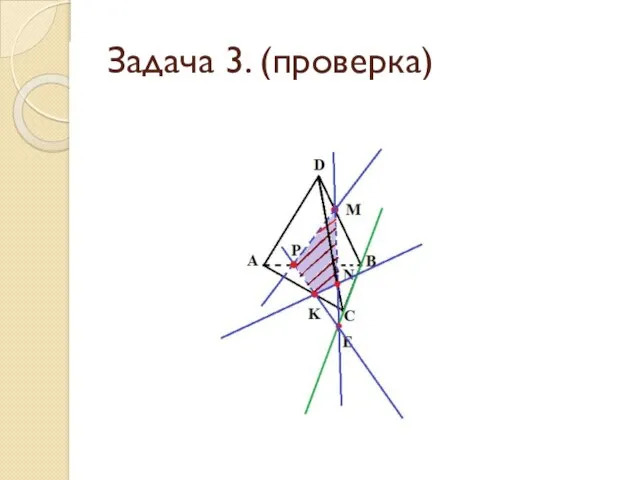
Задача 3. (проверка)

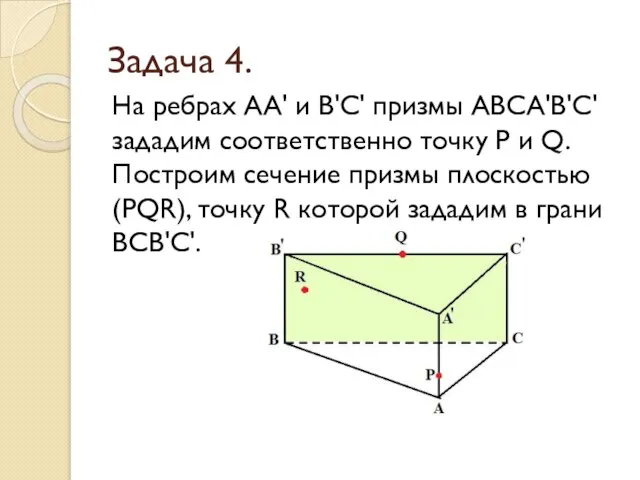
Задача 4.
На ребрах АА' и В'С' призмы АВСА'В'С' зададим соответственно точку P и Q. Построим сечение призмы плоскостью (PQR), точку R которой зададим в грани ВСВ'С'.

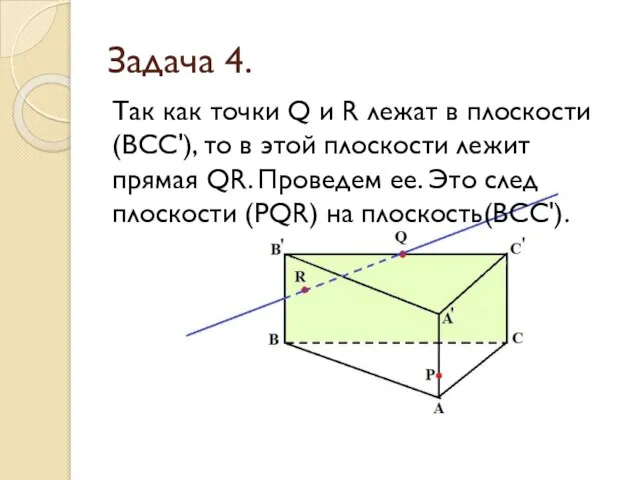
Задача 4.
Так как точки Q и R лежат в плоскости (ВСС'), то в этой плоскости лежит прямая QR. Проведем ее. Это след плоскости (PQR) на плоскость(ВСС').

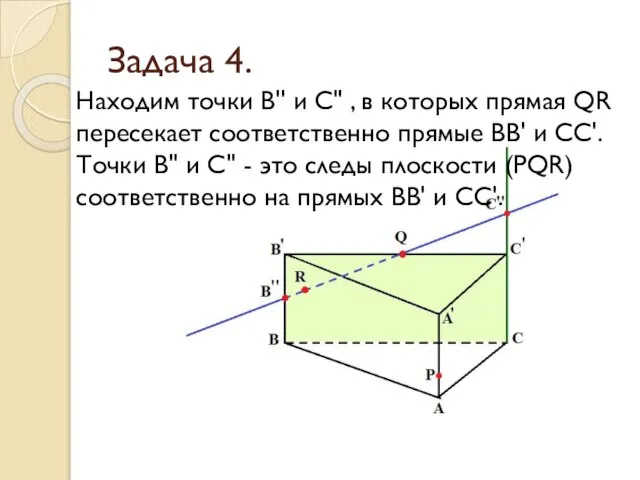
Задача 4.
Находим точки В'' и С'' , в которых прямая QR пересекает соответственно прямые ВВ' и СС'. Точки В'' и С'' - это следы плоскости (PQR) соответственно на прямых ВВ' и СС'.

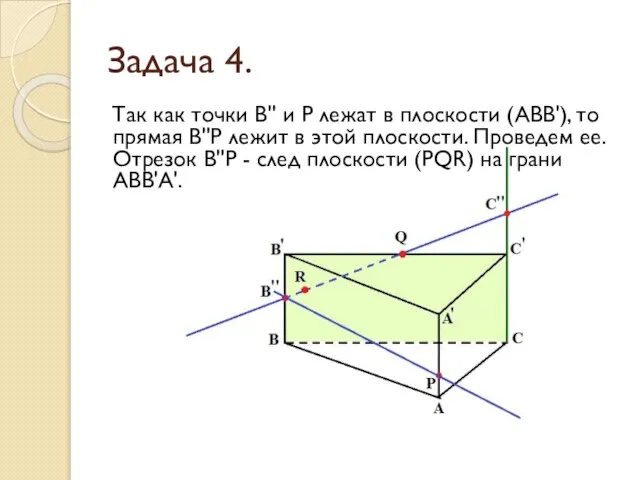
Задача 4.
Так как точки В'' и Р лежат в плоскости (АВВ'), то прямая В''Р лежит в этой плоскости. Проведем ее. Отрезок В''Р - след плоскости (PQR) на грани АВВ'А'.

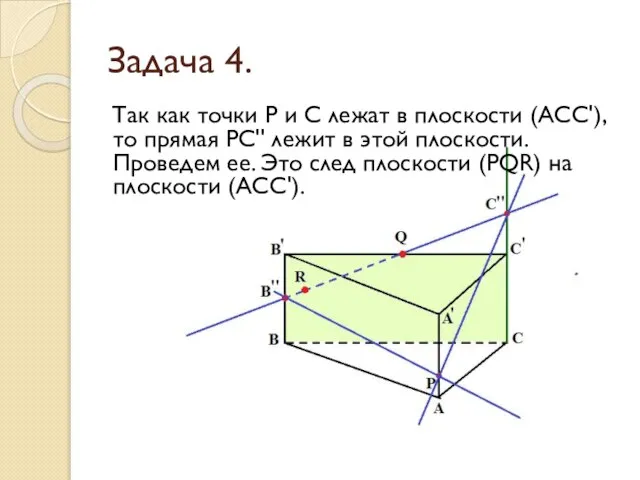
Задача 4.
Так как точки Р и С лежат в плоскости (АСС'), то прямая РС'' лежит в этой плоскости. Проведем ее. Это след плоскости (PQR) на плоскости (АСС').

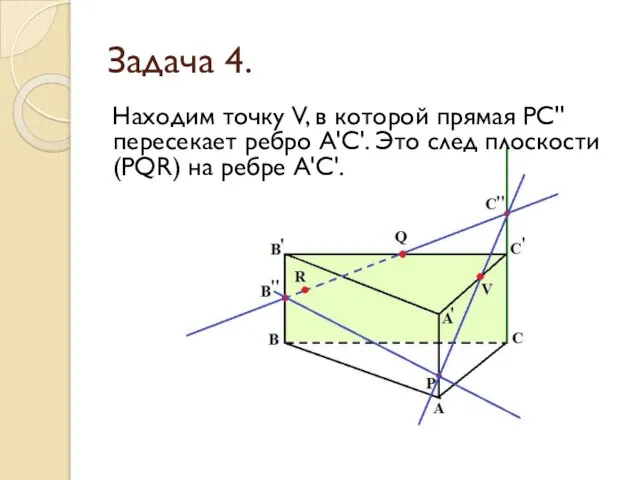
Задача 4.
Находим точку V, в которой прямая РС'' пересекает ребро А'С'. Это след плоскости (PQR) на ребре А'С'.

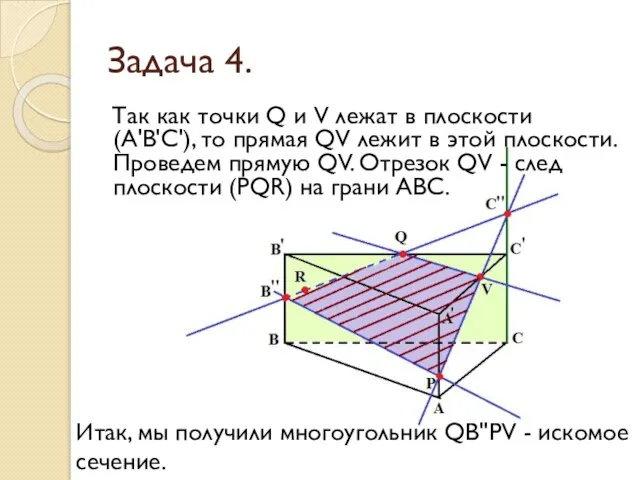
Задача 4.
Так как точки Q и V лежат в плоскости (А'В'С'), то прямая QV лежит в этой плоскости. Проведем прямую QV. Отрезок QV - след плоскости (PQR) на грани АВС.
Итак, мы получили многоугольник QB''PV - искомое сечение.

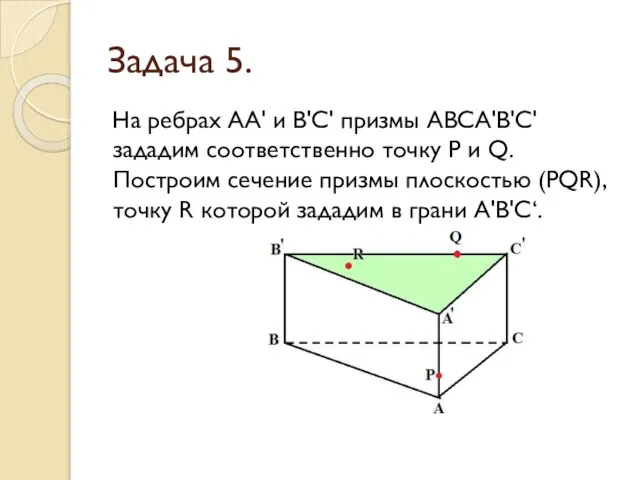
Задача 5.
На ребрах АА' и В'С' призмы АВСА'В'С' зададим соответственно точку P и Q. Построим сечение призмы плоскостью (PQR), точку R которой зададим в грани А'В'С‘.

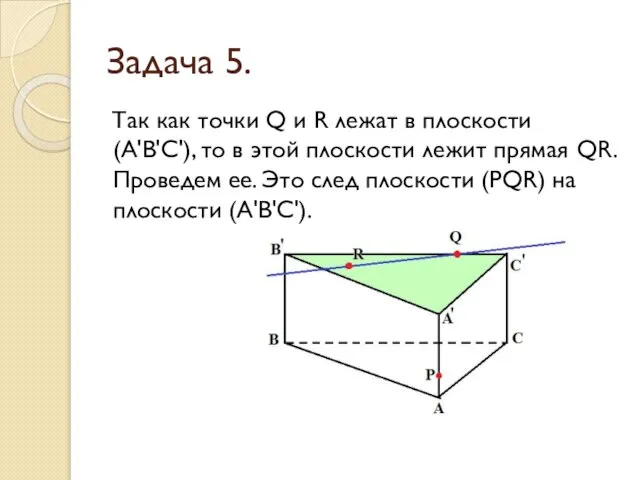
Задача 5.
Так как точки Q и R лежат в плоскости (А'В'С'), то в этой плоскости лежит прямая QR. Проведем ее. Это след плоскости (PQR) на плоскости (А'В'С').

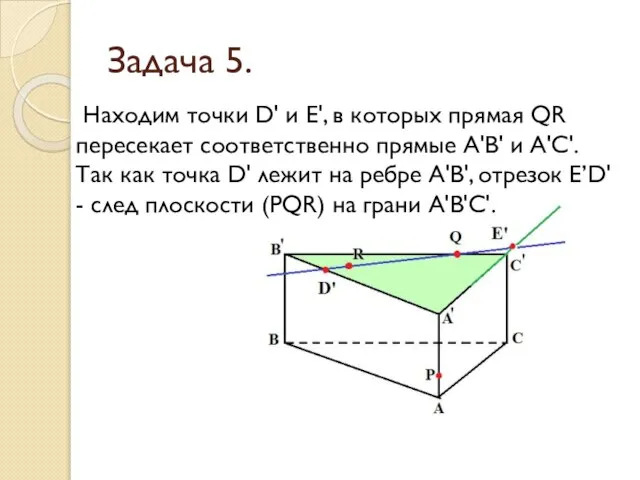
Задача 5.
Находим точки D' и Е', в которых прямая QR пересекает соответственно прямые А'В' и А'С'. Так как точка D' лежит на ребре А'В', отрезок Е’D' - след плоскости (PQR) на грани А'В'С'.

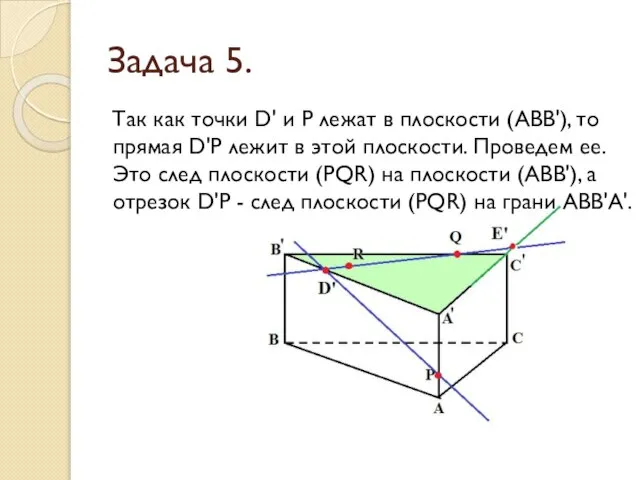
Задача 5.
Так как точки D' и P лежат в плоскости (АВВ'), то прямая D'P лежит в этой плоскости. Проведем ее. Это след плоскости (PQR) на плоскости (АВВ'), а отрезок D'P - след плоскости (PQR) на грани АВВ'А'.

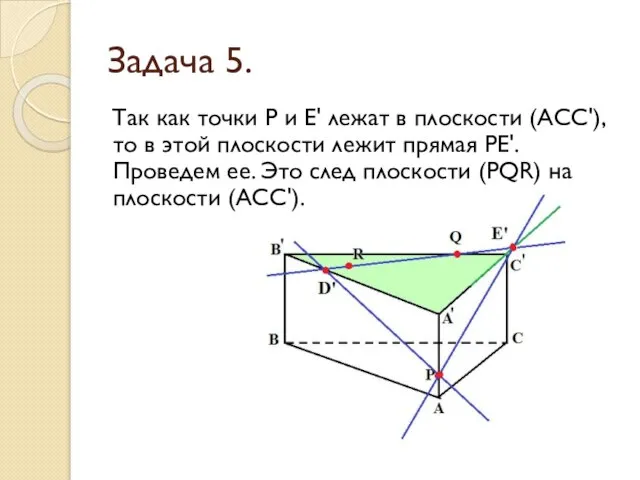
Задача 5.
Так как точки Р и Е' лежат в плоскости (АСС'), то в этой плоскости лежит прямая РЕ'. Проведем ее. Это след плоскости (PQR) на плоскости (АСС').

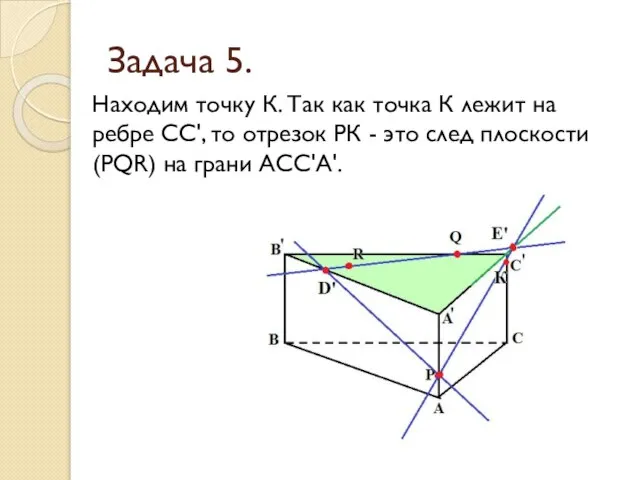
Задача 5.
Находим точку К. Так как точка К лежит на ребре СС', то отрезок РК - это след плоскости (PQR) на грани АСС'А'.