Дизъюнктивные нормальные формы (ДНФ). СДНФ

Определение 1
Конъюнкция логических переменных или их отрицаний называется элементарной конъюнкцией.
Пример
Определение 2
Высказывание называется дизъюнктивной нормальной формой (ДНФ), если оно представляет собою дизъюнкцию элементарных конъюнкций.
Общий вид ДНФ:
3. Дизъюнктивные нормальные формы (ДНФ)

Примеры

Теорема
Любое высказывание приводимо к ДНФ.
Схема приведения высказывания к ДНФ
Избавиться от импликации и эквивалентности, используя законы
16), 17)
2) Донести отрицания до переменных, используя законы Моргана.
3) Раскрыть скобки, используя дистрибутивные законы.
4) Упростить полученное высказывание.

Пример
Привести высказывание к ДНФ

5.Построение высказываний по таблице истинности. Совершенные дизъюнктивные нормальные формы (СДНФ)
Определение 1
Пусть – некоторое множество логических переменных. Элементарная конъюнкция, в которую входят все логические переменные, называется полной элементарной конъюнкцией относительно множества X .
Пример

Определение 2
Дизъюнктивная нормальная форма называется совершенной (СДНФ), если все составляющие ее элементарные конъюнкции являются полными.
Примеры
СДНФ

Приведение высказывания к СДНФ
Теорема
Высказывание, не являющееся тождественно ложным, приводимо к СДНФ.
Правило приведения высказывания к СДНФ
СДНФ содержит столько полных элементарных конъюнкций, сколько единиц в последнем столбце таблице истинности.
Вид каждой полной элементарной определяется соответствующим набором значений переменных, а именно, если переменная принимает значение 0, то над ней в полной элементарной конъюнкцией ставится отрицание, иначе – отрицание не ставится.

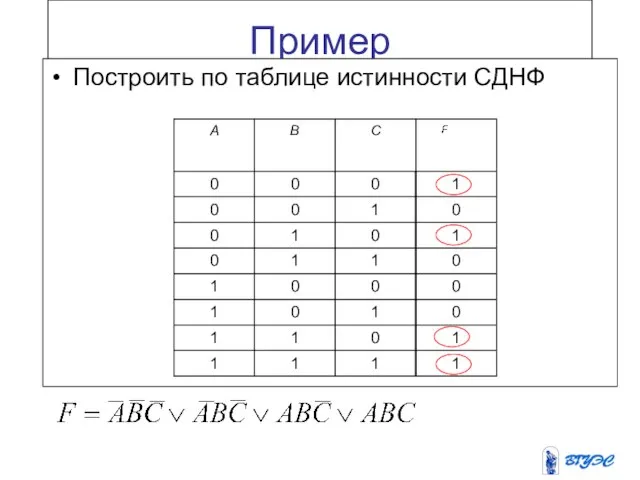
Пример
Построить по таблице истинности СДНФ

Задача
«Вернувшись домой, Мегрэ позвонил на набережную Орфевр.
- Говорит Мегрэ. Есть новости?
- Да, шеф. Поступили сообщения от инспекторов.
Торранс установил, что если Франсуа был пьян, то либо Этьен убийца, либо Франсуа лжет.
Жуссье считает, что или Этьен убийца, или Франсуа не был пьян и убийство произошло после полуночи.
Инспектор Люка просил передать Вам, что если убийство произошло после полуночи, то либо Этьен убийца, либо Франсуа лжет.
Затем звонила …
- Все. Спасибо. Этого достаточно. – Комиссар положил трубку. Он знал, что трезвый Франсуа никогда не лжет. Теперь он знал все.»
Что знал Мегрэ?

Решение задачи
Пусть
P=« Франсуа был пьян»
L=«Франсуа лжет»
I=«Этьен убийца»
U=«Убийство произошло после полуночи»
Тогда получим высказывание
Так как , то Этьен - убийца