Элементы комбинаторики. Решение простейших комбинаторных задач

Оценочный лист
Приложение 1
Оценочный лист
Фамилия, Имя обучающегося_______________________________
Группа_______________________________________________
Дата_________________________________________________

Математический диктант
В окружающем нас мире можно наблюдать события (явления), которые обязательно произойдут, если будет осуществлена определенная совокупность условий. Такие события принято называть…
Событие которое заведомо не произойдет, если будет осуществлена определенная совокупность условий, называется…
События, которые при осуществлении определенных условий могут произойти, а могут и не произойти. Такие события называются…
Два события называются …, если появление одного из них исключает появление другого. В противном случае события называются …
Совокупность условий, при осуществлении которых случайное событие может либо произойти, либо не произойти, будем называть … или…

Математический диктант
В окружающем нас мире можно наблюдать события (явления), которые обязательно произойдут, если будет осуществлена определенная совокупность условий. Такие события принято называть достоверными
Событие которое заведомо не произойдет, если будет осуществлена определенная совокупность условий, называется невозможным событием
События, которые при осуществлении определенных условий могут произойти, а могут и не произойти. Такие события называются случайными
Два события называются несовместными, если появление одного из них исключает появление другого. В противном случае события называются совместными
Совокупность условий, при осуществлении которых случайное событие может либо произойти, либо не произойти, будем называть испытанием или опытом

Тема занятия
Элементы комбинаторики. Решение простейших комбинаторных задач

Основная цель занятия
Знакомство с понятием «комбинаторика»,
понятиями: «размещения», «перестановки» и «сочетания»

Слово «комбинаторика» произошло от латинского слова «combinare», что означает «соединять, сочетать»
Комбинаторика- это раздел математики, в котором исследуются и решаются задачи выбора элементов из исходного множества и расположения их в некоторой комбинации, составляемой по заданным правилам

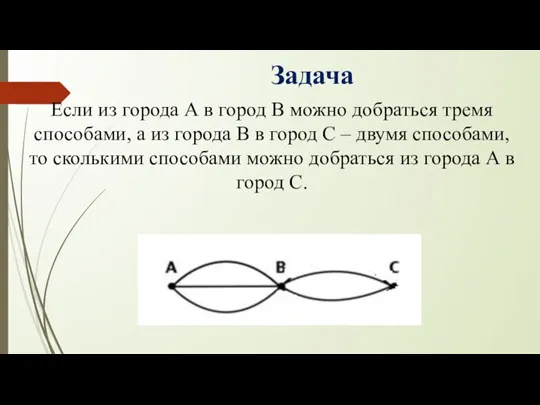
Задача
Если из города А в город В можно добраться тремя способами, а из города В в город С – двумя способами, то сколькими способами можно добраться из города А в город С.

Основное правило комбинаторики

Основные задачи комбинаторики
Размещения
Перестановки
Сочетания

Задача
В группе 20 обучающихся. Сколькими способами могут быть выбраны староста и заместитель старосты?

Формула числа размещении
где A – первая буква французского слова arrangement, что означает «размещение, приведение в порядок»

Определение

Определение

Формула числа перестановок
где P – первая буква французского слова permutation -перестановка

Задача
В группе из 20 обучающихся нужно выделить четырех для работы на определенном участке. Сколькими способами это можно сделать?

Определение

Формула числа сочетаний
где С - первая буква французского слова combination – сочетание.

Вывод
если порядок расположения элементов в выбираемых соединениях не важен, то для определения количества таких соединений используют формулу числа сочетаний . Например, выбор 4 обучающихся из группы в 20 студентов для выполнения одинаковой работы.
Если при выборе тех же студентов каждому из них выдаются разные задания, то порядок их выбора влияет на номер полученного задания, что является существенным. В этом случае следует использовать формулу числа размещений .

Задачи
Сколькими способами могут быть присуждены первая, вторая и третья премии трём лицам из 10 соревнующихся?
Ответ: размещения
Сколькими способами можно расставить на одной полке шесть различных книг?
Ответ: перестановки
Сколько матчей будет сыграно в футбольном чемпионате с участием 16 команд, если каждые две команды встречаются между собой один раз?
Ответ: сочетания

Определите какую формулу необходимо применить: размещения, перестановки или сочетания
Сколькими различными способами могут сесть на скамейку
а) 5 человек;
б) 7 человек
Сколько различных трехцветных флагов с тремя горизонтальными полосами можно получить, используя красный, синий и белый цвета?
Учащиеся должны посетить во вторник по расписанию 5 уроков по следующим предметам: литература, алгебра, география, физкультура и биология. Сколькими способами можно составить расписание на этот день, чтобы физкультура была пятым уроком?

Определите какую формулу необходимо применить: размещения, перестановки или сочетания
На станции имеется 8 запасных путей. Сколькими способами можно расставить на них четыре поезда.
Сколькими способами можно изготовить трёхцветный флаг с горизонтальными полосами из материала, имеющего 5 различных цветов?
Учащиеся школы изучают 12 различных предметов. Сколькими способами можно составить расписание уроков на один день, чтобы в нём было 5 различных предметов?

Домашнее задание
Сколько четырёхзначных чисел можно составить из цифр 1, 2, 5, 7, если каждая цифра может использоваться только один раз?
Чтобы открыть сейф, нужно набрать шифр, содержащий определённую последовательность из цифр 1, 2, 3, 4, 5, 6, и другой шифр, содержащий последовательность из букв a, b, c, d, в которых буквы и цифры не повторяются. Сколько существует комбинаций, при которых сейф НЕ открывается?
Из цифр 1, 2, 3, 4, 5, 6 составьте четырёхзначные числа, в которых все цифры различны, а первой цифрой является 1 и второй – 3. Сколько таких чисел?
В вагоне имеется 10 свободных мест. В вагон вошли 6 пассажиров. Сколькими способами они могут разместиться в этом вагоне на свободных местах?