Содержание
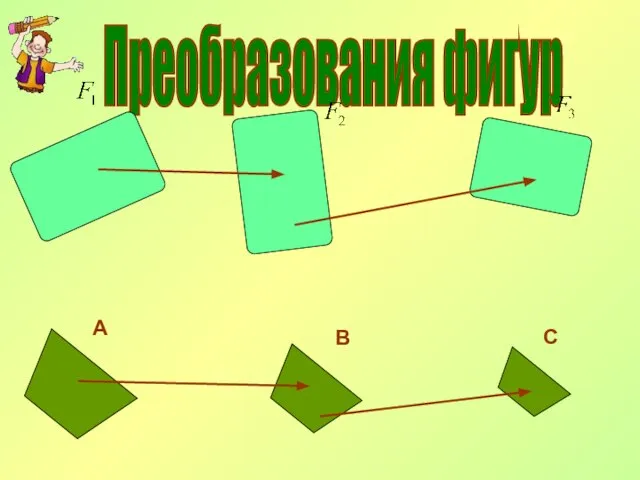
- 2. Преобразования фигур Движение
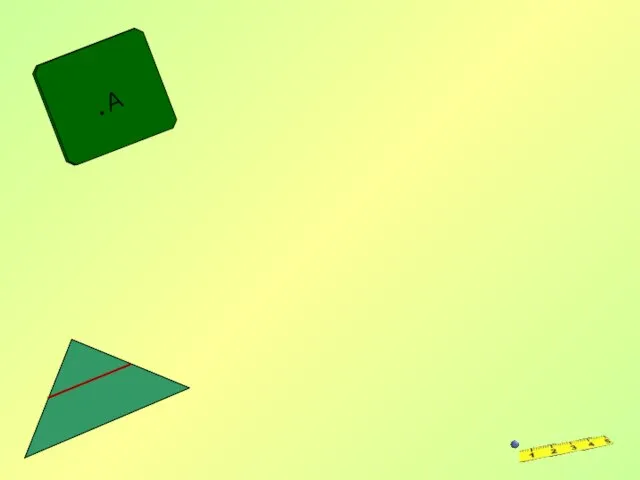
- 3. Преобразования фигур А В С
- 4. Движение Преобразование одной фигуры в другую, при котором сохраняется расстояние между точками называется движением.
- 5. .А .А
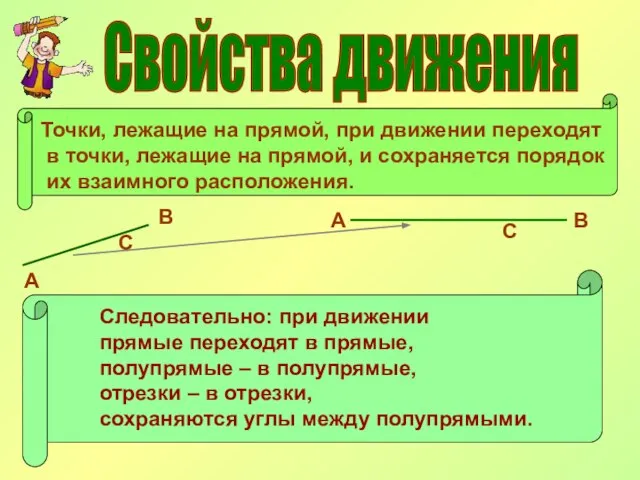
- 6. Свойства движения Точки, лежащие на прямой, при движении переходят в точки, лежащие на прямой, и сохраняется
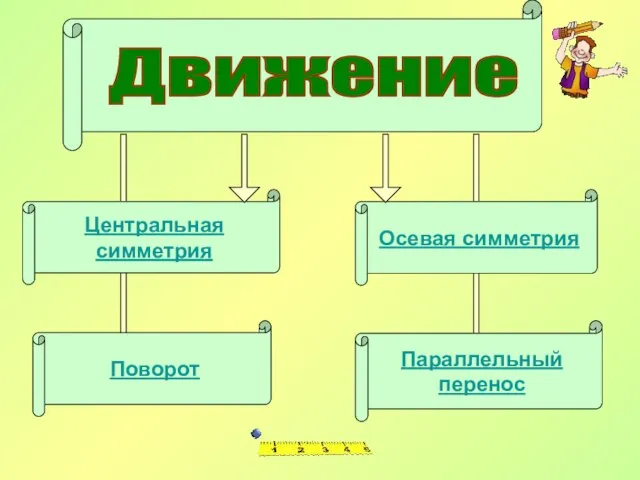
- 7. Движение Центральная симметрия Поворот Осевая симметрия Параллельный перенос
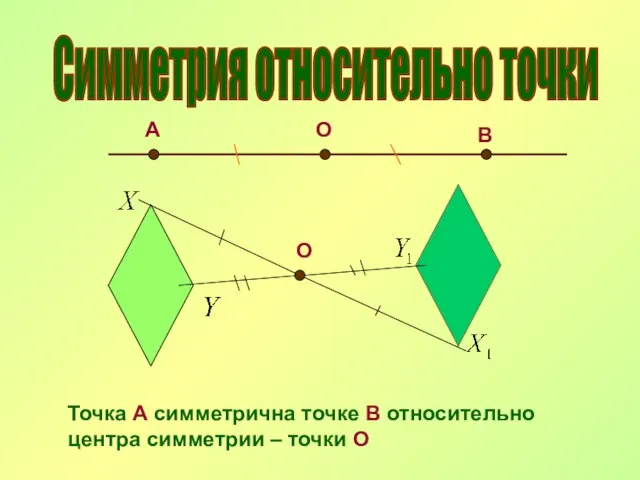
- 8. Симметрия относительно точки О А В О Точка А симметрична точке В относительно центра симметрии –
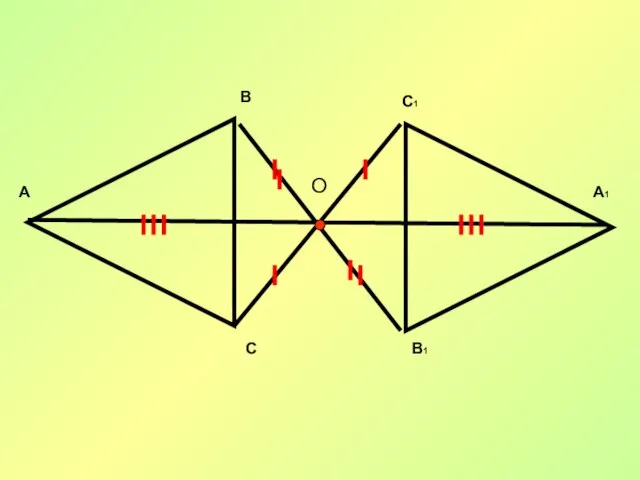
- 9. O А С В А1 В1 С1
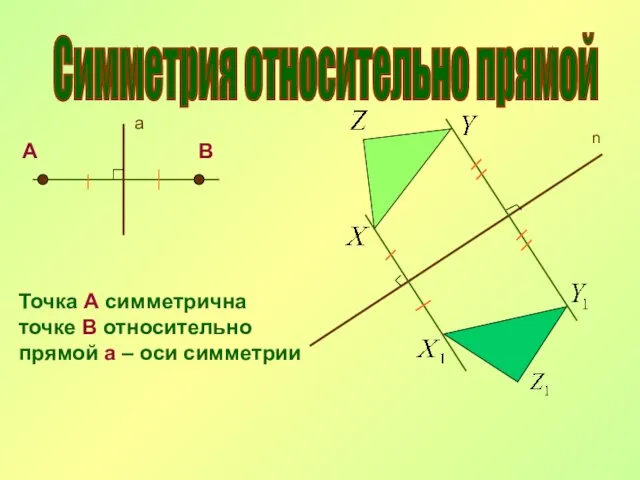
- 11. Симметрия относительно прямой а А В Точка А симметрична точке В относительно прямой а – оси
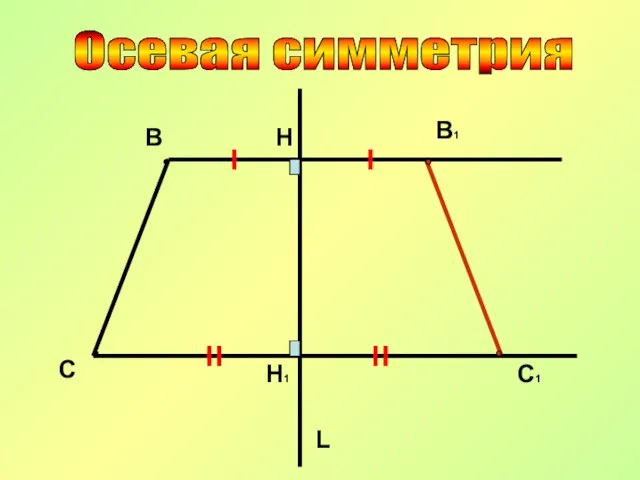
- 12. Осевая симметрия L C B B1 C1 H H1
- 13. Проведите луч АО Измерьте отрезок АО Из точки О отложите отрезок ОА1 равный, отрезку АО Проведите
- 15. ЭШЕР МОРИС Симметрия в искусстве Голландский художник Морис Корнелиус Эшер (Maurits Cornelis Escher) родился 17 июня
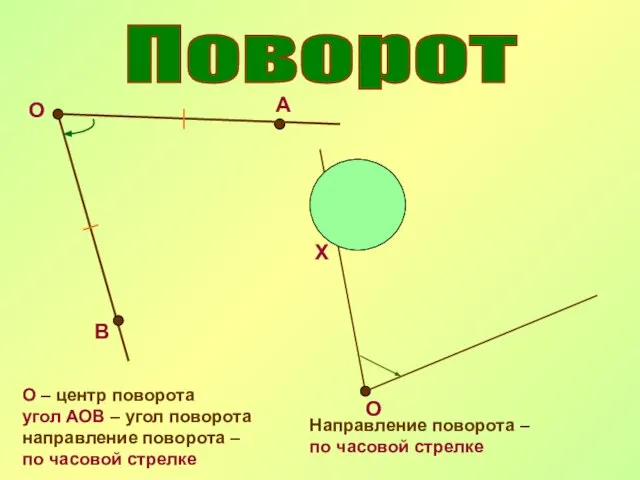
- 16. Поворот О А В О – центр поворота угол АОВ – угол поворота направление поворота –
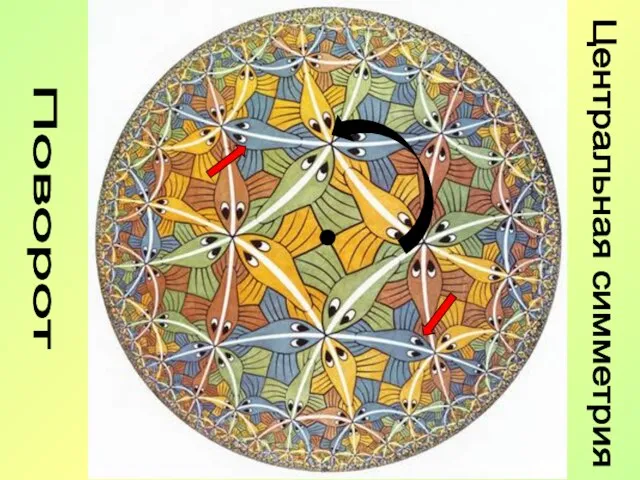
- 18. Поворот Центральная симметрия
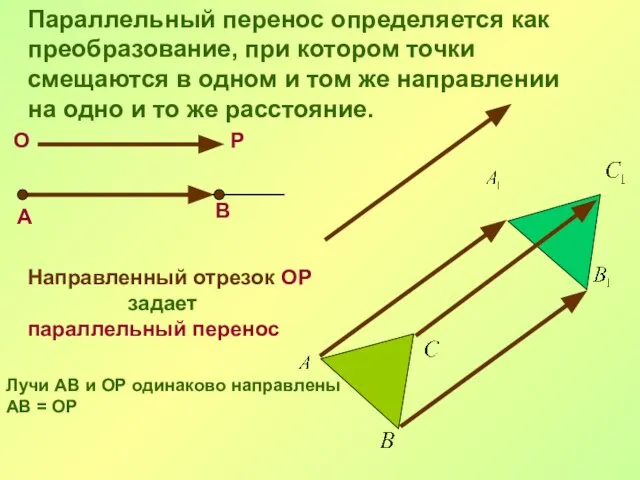
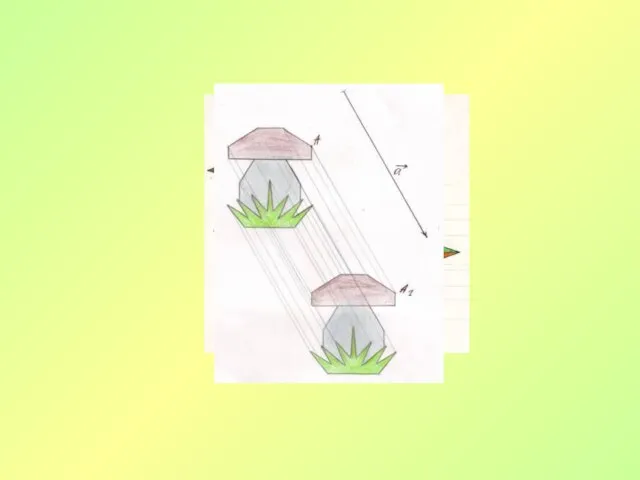
- 19. Параллельный перенос Преобразование фигуры F, при котором ее произвольная точка (х; у) переходит в точку (х+а;
- 20. В О Р А Направленный отрезок ОР задает параллельный перенос Лучи АВ и ОР одинаково направлены
- 22. Композиция движений
- 23. Параллельный перенос Если всмотреться в картину, то можно увидеть как образ человека переходит в тот же
- 24. При создании картины использовалась осевая симметрия "Ангелы и дьяволы" А В L
- 27. Скачать презентацию












 Многогранники и их основные свойства
Многогранники и их основные свойства Формула сложных процентов в ЕГЭ. 11 класс
Формула сложных процентов в ЕГЭ. 11 класс Сокращенное умножение многочленов
Сокращенное умножение многочленов Переместительный и сочетательный законы сложения
Переместительный и сочетательный законы сложения Практика. Дискретная математика
Практика. Дискретная математика Презентация на тему Софья Васильевна Ковалевская
Презентация на тему Софья Васильевна Ковалевская  Уравнение прямой
Уравнение прямой Сумма углов треугольника. Решение задач
Сумма углов треугольника. Решение задач Координаты вектора
Координаты вектора Принак подобия треугольников. Урок 33
Принак подобия треугольников. Урок 33 Миллиметр. В каких числах сумма цифр равна 5?
Миллиметр. В каких числах сумма цифр равна 5? Классификация многоугольников по числу углов
Классификация многоугольников по числу углов Задача предельного типа. Мир арифметики
Задача предельного типа. Мир арифметики Презентация на тему Развивающие задачи для 5-6 классов
Презентация на тему Развивающие задачи для 5-6 классов  Переместительное свойство умножения
Переместительное свойство умножения Свойства умножения. 5 класс
Свойства умножения. 5 класс Математический турнир Умники и умницы
Математический турнир Умники и умницы Исследование операций. Принятие решений и неопределенность. Лекция 3
Исследование операций. Принятие решений и неопределенность. Лекция 3 11 клас призма
11 клас призма Метод Гаусса решения систем линейных уравнений
Метод Гаусса решения систем линейных уравнений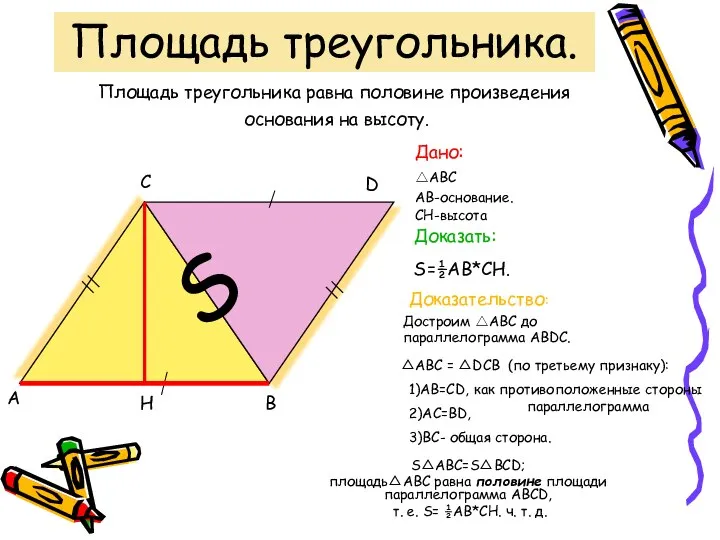 Площадь треугольника
Площадь треугольника Параллельные прямые
Параллельные прямые Презентация на тему Построение точек по заданным координатам
Презентация на тему Построение точек по заданным координатам  Как может математика помочь быть здоровым?
Как может математика помочь быть здоровым? Состав чисел в приделах 10. Закрепление изученного материала
Состав чисел в приделах 10. Закрепление изученного материала Корень n-ой степени
Корень n-ой степени Шестое математическое действие
Шестое математическое действие Подготовка к ЕГЭ. Тестирование
Подготовка к ЕГЭ. Тестирование