квадратов двух других сторон, то треугольник прямоугольный.
Дано : АВС
АВ2 = АС2 + ВС2
Доказать , что ∠ С = 90 .
Доказательство :
Пусть в треугольнике АВС АВ2 = АС2 + ВС2. Докажем , что угол С прямой. Рассмотрим прямоугольный треугольник А1 В1 С1 с прямым углом С1 , у которого А1 С1 = АС и В1 С1 = ВС. По теореме Пифагора А1В1 2 = А1С12 + В1С12 , и , значит А1В12 = АС2 + ВС2.
Но АС 2 + ВС2 = АВ2 по условию теоремы. Следовательно, А1В12 = АВ2 , откуда А1В1 = АВ. Треугольники АВС и А1В1С1 равны по трем сторонам, поэтому угол С равен углу С1, т. е. треугольник АВС прямоугольный с прямым углом С. Теорема доказана


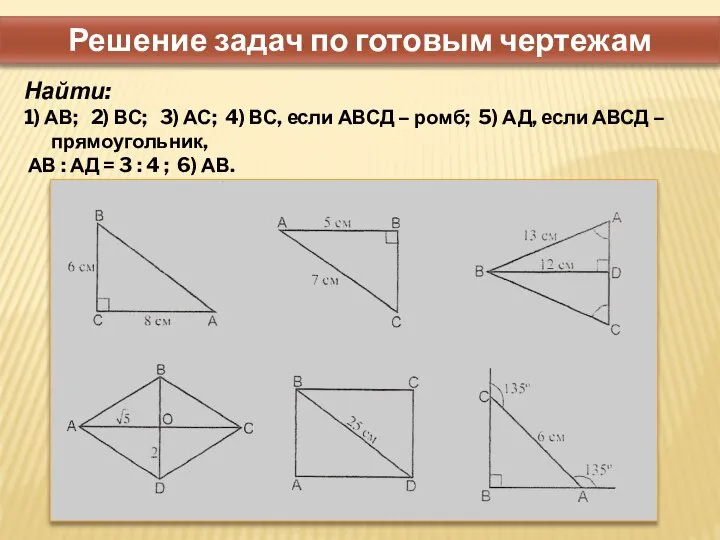







 Этапы создания математических моделей
Этапы создания математических моделей Обработка и анализ результатов моделирования
Обработка и анализ результатов моделирования Показательная функция. Построение и преобразование графика функции
Показательная функция. Построение и преобразование графика функции Производная функции
Производная функции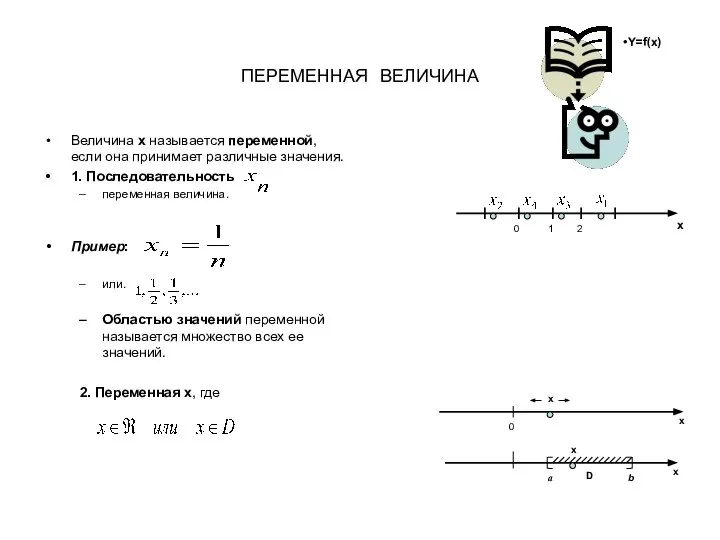 Понятие функции, предел
Понятие функции, предел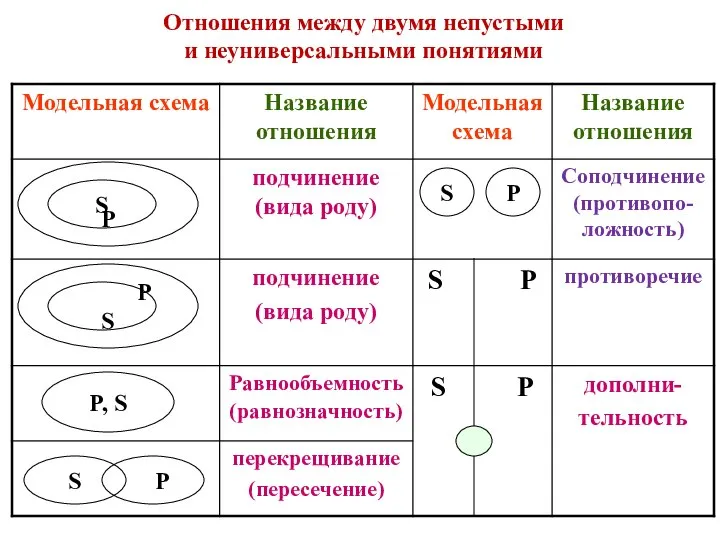 Отношения между двумя непустыми и неуниверсальными понятиями. Модельная схема
Отношения между двумя непустыми и неуниверсальными понятиями. Модельная схема Узоры и орнаменты на посуде
Узоры и орнаменты на посуде ГИА - 2016. Задачи №9,10,11,12
ГИА - 2016. Задачи №9,10,11,12 Векторный анализ - теория поля. Векторное поле. Лекция 17
Векторный анализ - теория поля. Векторное поле. Лекция 17 Решение иррациональных уравнений
Решение иррациональных уравнений Осевая симметрия
Осевая симметрия Презентация на тему МЕТОДЫ РЕШЕНИЯ НЕРАВЕНСТВ С ОДНОЙ ПЕРЕМЕННОЙ (ТИПОВЫЕ ЗАДАНИЯ С3) - 1
Презентация на тему МЕТОДЫ РЕШЕНИЯ НЕРАВЕНСТВ С ОДНОЙ ПЕРЕМЕННОЙ (ТИПОВЫЕ ЗАДАНИЯ С3) - 1  Сложение вида +2, +3
Сложение вида +2, +3 Личные местоимения
Личные местоимения Поможем Айболиту
Поможем Айболиту Готовимся к ОГЭ по математике
Готовимся к ОГЭ по математике Логарифмические неравенства
Логарифмические неравенства Математика в профессиях
Математика в профессиях Умножение многочлена на многочлен
Умножение многочлена на многочлен Итоговое повторение курса геометрии 8 класса
Итоговое повторение курса геометрии 8 класса Исследование золотого сечения и его применения в окружающем нас мире
Исследование золотого сечения и его применения в окружающем нас мире Матрица размера m x n
Матрица размера m x n Линейная алгебра. Матрицы. Основные понятия. Действия над матрицами. Поиск обратной матрицы
Линейная алгебра. Матрицы. Основные понятия. Действия над матрицами. Поиск обратной матрицы Число Пи вокруг нас
Число Пи вокруг нас Вписанная окружность в треугольник
Вписанная окружность в треугольник Приемы вычитания с переходом на десяток
Приемы вычитания с переходом на десяток Системы неравенств с одной переменной
Системы неравенств с одной переменной Решение логарифмических уравнений
Решение логарифмических уравнений