Элементы математической статистики. Теория вероятностей

Теория вероятностей — раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.
Предметом теории вероятностей является изучение вероятностных закономерностей массовых однородных случайных событий.
Математическая статистика – раздел математики, изучающий методы сбора, систематизации и обработки результатов наблюдений с целью выявления статистических закономерностей.
Предмет математической статистики – изучение случайных величин по результатам наблюдений.

Задачи математической статистики
Первая задача математической статистики - определить способы сбора данных и группировки данных, полученных в результате наблюдений или в результате специально поставленных экспериментов.
Вторая задача математической статистики - разработать методы анализа статистических данных в зависимости от целей исследования.

Методы анализа статистических данных должны обеспечить:
1. Оценку:
- неизвестной вероятности события;
- неизвестной функции распределения;
- параметров распределения, вид которого известен;
- зависимости случайной величины от одной или нескольких случайных величин и др.;
2. Проверку статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого известен.

2. История становления математической статистики как науки
(Самостоятельно)

3. Генеральная и выборочная совокупности
Генеральная совокупность – это множество всех объектов, которые имеют качества, свойства, интересующие исследователя.
Например: население страны, животные и растения на определенной территории, избиратели (т.е. люди, имеющие право голосовать), школьники, студенты, товары и т.д.
Иногда проводят сплошное обследование, т. е. обследуют каждый из объектов совокупности относительно признака, которым интересуются. Например: перепись населения, проверка качества изделия.

На практике, однако, сплошное обследование применяют сравнительно редко.
Причины:
1. Очень большое число объектов, поэтому сплошное обследование физически невозможно.
2. Большие материальные, финансовые и временные затраты.
3. Обследование объекта связано с его уничтожением (испытание надежности автомобиля, точность попадания боевых ракет).
В таких случаях случайно отбирают из всей совокупности ограниченное число объектов и подвергают их изучению.
Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных объектов для изучения.
Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности. Например, если из 1000 деталей отобрано для обследования 100 деталей, то объем генеральной совокупности N=1000, а объем выборки n=100.

4. Повторная и бесповторная выборки.
Репрезентативная выборка
Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность.
Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.
На практике обычно пользуются бесповторным случайным отбором.

Для того чтобы по данным выборки можно было до-статочно уверенно судить об интересующем признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно его представляли.
Это требование коротко формулируют так: выборка должна быть репрезентативной (представительной ).
В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если ее осуществить случайно: каждый объект выборки отобран случайно из генеральной совокупности, если все объекты имеют одинаковую вероятность попасть в выборку.

Названием "закон больших чисел" объединена группа теорем, устанавливающих устойчивость средних результатов большого количества случайных явлений и объясняющих причину этой устойчивости.
1. Теорема Бернулли.
2. Теорема Пуассона.
3. Теорема Муавра-Лапласа.
4. Предельные теоремы теории вероятностей (интегральная теорема Лапласа).
5. Центральная предельная теорема (теорема Леонтьева).
6. Неравенство Чебышева.
"Закон больших чисел" утверждает, что при определенных, достаточно общих, условиях, с увеличением числа случайных величин их среднее арифметическое стремится к среднему арифметическому математических ожиданий и перестает быть случайным.

5. Способы отбора (формирование выборки)
На практике применяются различные способы отбора. Принципиально эти способы можно подразделить на два вида:
1. Отбор, не требующий расчленения генеральной совокупности на части. Сюда относятся: а) простой случайный бесповторный отбор; б) простой случайный повторный отбор.
2. Отбор, при котором генеральная совокупность разбивается на части. Сюда относятся: а) типический отбор; б) механический отбор; в) серийный отбор.

Простым случайным называют такой отбор, при котором объекты извлекают по одному из всей генеральной совокупности. Осуществить простой отбор можно различными способами.
Например, для извлечения n объектов из генеральной совокупности объема N поступают так:
1) присваивают номер каждому объекту от 1 до N;
2) выписывают номера от 1 до N на карточках, которые тщательно перемешивают;
3) наугад вынимают одну карточку; объект, имеющий одинаковый номер с извлеченной карточкой, подвергают обследованию;
4) затем карточку возвращают в пачку и процесс повторяют, т. е. карточки перемешивают, наугад вынимают одну из них и т. д. Так поступают n раз; в итоге получают простую случайную повторную выборку объема n.
Если извлеченные карточки не возвращать в пачку, то выборка является простой случайной бесповторной.

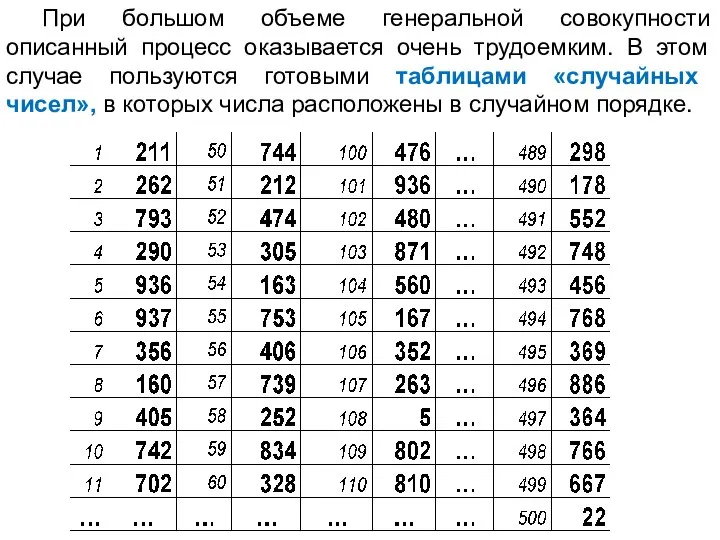
При большом объеме генеральной совокупности описанный процесс оказывается очень трудоемким. В этом случае пользуются готовыми таблицами «случайных чисел», в которых числа расположены в случайном порядке.

Для того чтобы отобрать, например, 500 студентов из пронумерованной генеральной совокупности 9000 (обще число студентов в ВУЗе), открывают любую страницу таблицы случайных чисел и выписывают подряд 500 чисел; в выборку попадают те объекты, номера которых совпадают с выписанными случайными числами.
Если окажется, что случайное число таблицы превышает число 9000, то такое случайное число пропускают.
При осуществлении бесповторной выборки случайные числа таблицы, уже встречавшиеся ранее, следует также пропустить.

Типическим называют отбор, при котором объекты отбираются не из всей генеральной совокупности, а из каждой ее «типической» части (группы).
Например,
1) при обследованиях населения такими группами могут быть районы, социальные, возрастные или образовательные группы и т.д.
2) при оценке качества отбирают детали каждого станка в отдельную группу.
Типическим отбором пользуются тогда, когда обследуемый признак заметно колеблется в различных типических частях генеральной совокупности.
Различают пропорциональный и непропорциональный типический отбор.

Механическим называют отбор, при котором генеральную совокупность «механически» делят на столько групп, сколько объектов должно войти в выборку, а из каждой группы отбирают один объект.
Например, если нужно отобрать 20% изготовленных на станке деталей, то отбирают каждую пятую деталь; если требуется отобрать 5% деталей, то отбирают каждую двадцатую деталь, и т. д.
Иногда механический отбор может не обеспечить репрезентативности выборки. Например, если отбирают каждую двадцатую обтачиваемую деталь, причем сразу же после отбора производят замену резца, то отобранными окажутся все детали, обточенные затупленными резцами. В таком случае следует устранить совпадение ритма отбора с ритмом замены резца, для чего надо отбирать, скажем, каждую десятую деталь из двадцати обточенных.

Серийным называют отбор, при котором объекты отбирают из генеральной совокупности не по одному, а «сериями», которые подвергаются сплошному обследованию.
Например:
1) если изделия изготовляются большой группой станков-автоматов, то подвергают сплошному обследованию продукцию только нескольких станков.
2) при оценке успеваемости выбирается школа или ВУЗ и все ученики или студенты Этой школы или ВУЗа подвергаются сплошному обследованию.
Серийным отбором пользуются тогда, когда обследуемый признак колеблется в различных сериях незначительно.
Например, успеваемость существенно не изменяется в зависимости от школы (ВУЗа), от региона местоположения.

На практике часто применяется комбинированный отбор, при котором сочетаются указанные выше способы.
Например, иногда разбивают генеральную совокупность на серии одинакового объема, затем простым случайным отбором выбирают несколько серий и, наконец, из каждой серии простым случайным отбором извлекают отдельные объекты.

Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот.
Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал).
В теории вероятностей под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике - соответствие между наблюдаемыми вариантами и их частотами, или относительными частотами.

Пример. Задано распределение частот выборки объема n = 20:
хi: 2 6 12
ni: 3 10 7
Определить распределение относительных частот.
Решение. Найдем относительные частоты, для чего разделим частоты на объем выборки:
W1 = 3/20=0,15; W2 = 10/20 = 0,50; W3 = 7/20=0,35.
Запишем распределение относительных частот:
хi: 2 6 12
Wi: 0,15 0,50 0,35
Контроль: 0,15 + 0,50 + 0,35= 1.

7. Эмпирическая функция распределения
Пусть известно статистическое распределение частот количественного значения случайной величины X. Введем обозначения: nх—число наблюдений, при которых наблюдалось значение признака, меньшее x; n—общее число наблюдений (объем выборки).
При этом относительная частота события X<х равна nх/n. Если х изменяется, то, вообще говоря, изменяется и относительная частота, т. е. относительная частота nх/n есть функция от х.
Так как эта функция находится эмпирическим (опытным) путем, то ее называют эмпирической.

Определение: Эмпирической функцией распределения (функцией распределения выборки) называют функцию F*(х), определяющую для каждого значения х относительную частоту события X < х.
Итак, по определению,
F*(х) = nх/n,
где nх - число вариант, меньших х; n - объем выборки.
Таким образом, для того чтобы найти, например, F*(x2), надо число вариант, меньших х2, разделить на объем выборки:
F*(x2) = nх2/n.

Определение: Функцию распределения F(х) генеральной совокупности называют теоретической функцией распределения.
Различие между эмпирической и теоретической функциями состоит в том, что теоретическая функция F(х) определяет вероятность события X<х, а эмпирическая функция F*(x) определяет относительную частоту этого же события.
Из теоремы Бернулли следует, что относительная частота события X<х, т. е. F*(x) стремится по вероятности к вероятности F(х) этого события. Другими словами, при больших n значения функций F*(х) и F(х) мало отличаются одно от другого в том смысле, что limP[|F(x) - F*(х)I<ε] = 1 (ε>0).
Отсюда следует целесообразность использования эмпирической функции распределения выборки для приближенного представления теоретической (интегральной) функции распределения генеральной совокупности.

Эмпирическая функция распределения случайной величины X определяется следующей формулой
Основные свойства функции F*(x).
1. Значения эмпирической функции принадлежат отрезку 0 ≤ F*(x) ≤ 1.
2. F*(x) – неубывающая ступенчатая функция.
3. Если x1 — наименьшая варианта, то F*(x) = 0, для x ≤ x1.
4. Если xk — наибольшая варианта, то F*(x) = 1, для x > xk.

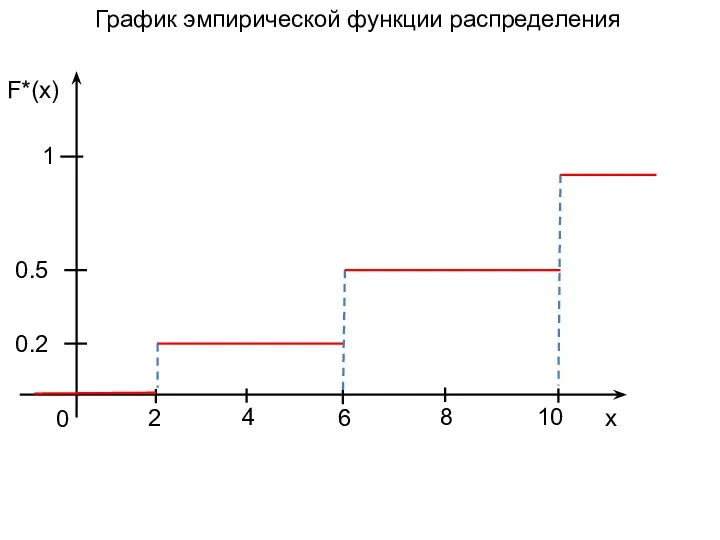
Пример. Построить эмпирическую функцию по данному распределению выборки:
варианты хi: 2 6 10
частоты ni: 12 18 30
Решение. Найдем объем выборки n: 12 + 18 + 30 = 60.
1. Наименьшая варианта х1=2, следовательно, F*(x)=0 при х≤2 (или x≤х1).
2. Значение X<6, а именно х1=2, наблюдалось 12 раз, следовательно, F*(х) = 12/60 = 0,2 при 2<х<6.
3. Значения X < 10, а именно х1 = 2 и х2 = 6, наблюдались 12+18 = 30 раз, следовательно, F*(x) = 30/60 = 0,5 при 6<х<10.
4. Так как х1=10 - наибольшая варианта, то при F*(x) = 0 при х>10.
Искомая эмпирическая функция

График эмпирической функции распределения
0
F*(x)
x
2
4
6
8
10
0.2
0.5
1

8. Полигон и гистограмма
Для наглядности строят различные графики статистического распределения и, в частности, полигон и гистограмму.
Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат - соответствующие им частоты ni. Точки (xi; ni) соединяют отрезками прямых и получают полигон частот.
Для построения полигона относительных частот на оси абсцисс откладывают варианты xi, а на оси ординат - соответствующие им относительные частоты ni/n. Точки (xi;ni/n) соединяют отрезками прямых и получают полигон относительных частот.

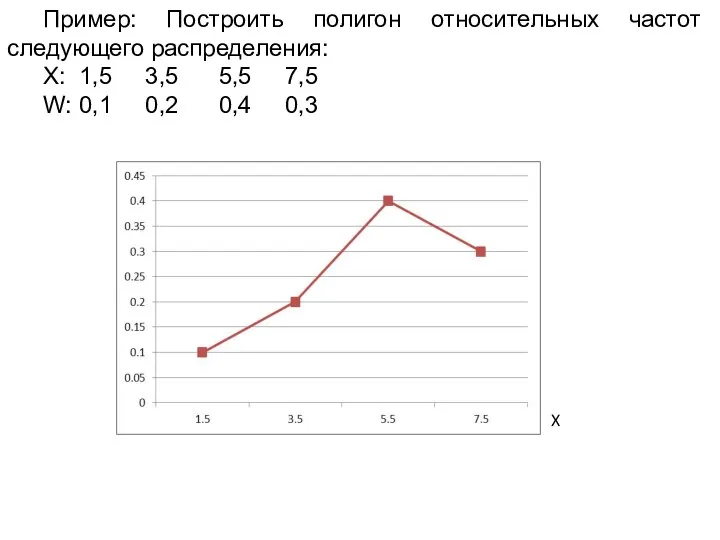
Пример: Построить полигон относительных частот следующего распределения:
X: 1,5 3,5 5,5 7,5
W: 0,1 0,2 0,4 0,3
X

В случае непрерывного признака целесообразно строить гистограмму.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению ni/h (плотность частоты).
Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы (h), а над ними проводят отрезки, параллельные оси абсцисс на расстоянии ni/h.
Площадь i-го частичного прямоугольника равна h*ni/h=ni - сумме частот вариант i-го интервала.
Cледовательно, площадь гистограммы частот равна сумме всех частот, т. е. объему выборки.