Содержание
- 2. Тема урока: Решение задач. Цель урока: 1)Рассмотреть решение задач с помощью теоремы Пифагора. 2) Развивающая: развитие
- 3. Вступительное слово учителя: объявление целей и задач урока. Проверка домашнего задания. Решение задач. Тестирование. Сообщение об
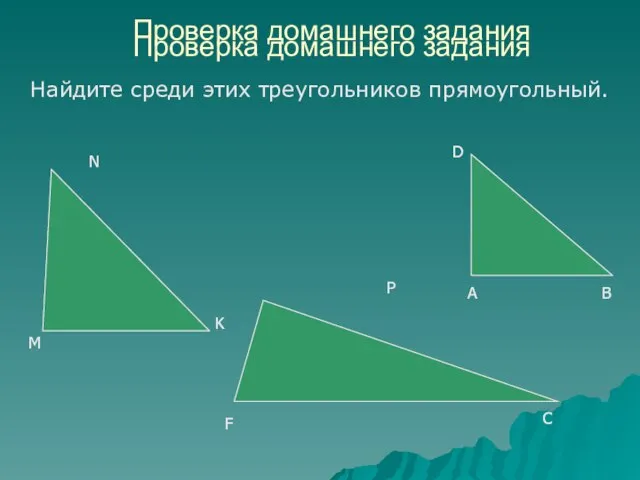
- 4. Проверка домашнего задания Найдите среди этих треугольников прямоугольный. Проверка домашнего задания
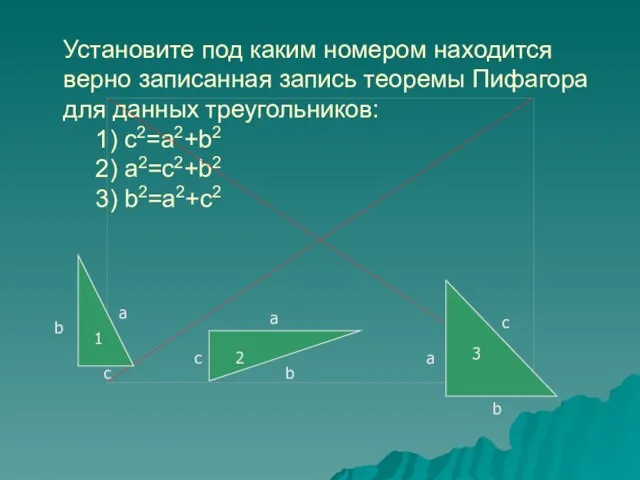
- 5. Установите под каким номером находится верно записанная запись теоремы Пифагора для данных треугольников: 1) c2=a2+b2 2)
- 6. Если a, b, c – стороны треугольника, то определите какие из данных треугольников являются прямоугольными: 1)
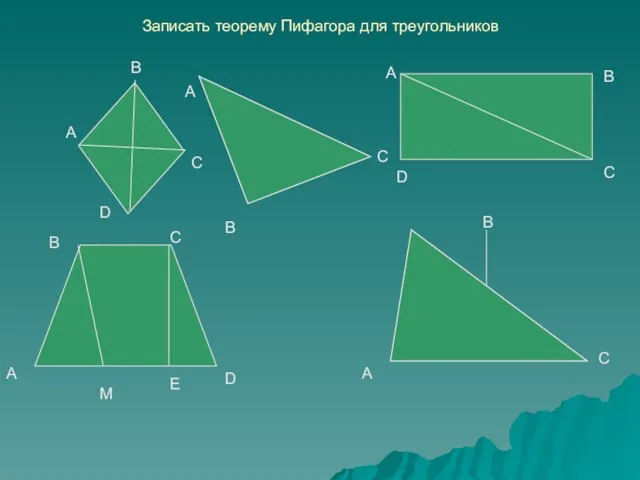
- 7. Записать теорему Пифагора для треугольников A B A B C D C A B C D
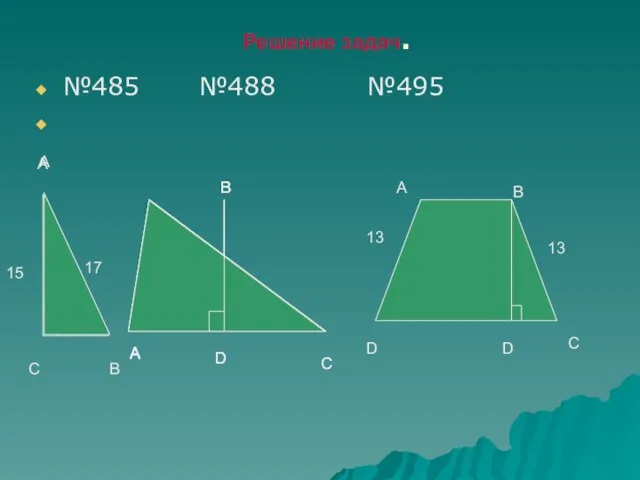
- 8. Решение задач. №485 №488 №495 A B C 17 15 A B C D D A
- 9. Пифагор Самосский Древнегреческий мыслитель, религиозный и политический деятель, основатель пифогареизма. Пифагор покинул родной остров Самос в
- 10. Теорема Пифагора. Теорема геометрии, устанавливающая связь между сторонами прямоугольного треугольника. Теорема была, по-видимому, известна до Пифагора(6
- 11. Итоги урока. При решении задач с применением теоремы Пифагора нужно: 1)указать прямоугольный треугольник; 2)записать для него
- 13. Скачать презентацию






 Думаємо колективно, працюємо оперативно, сперечаємось доказово – це для всіх обов'язково
Думаємо колективно, працюємо оперативно, сперечаємось доказово – це для всіх обов'язково Доли. Устный счет
Доли. Устный счет Доли. Обыкновенные дроби
Доли. Обыкновенные дроби Элементы теории фредгольмовых отображений
Элементы теории фредгольмовых отображений Упрощение выражений. Урок-сказка
Упрощение выражений. Урок-сказка Решение уравнений
Решение уравнений Признаки классификации статистической сводки
Признаки классификации статистической сводки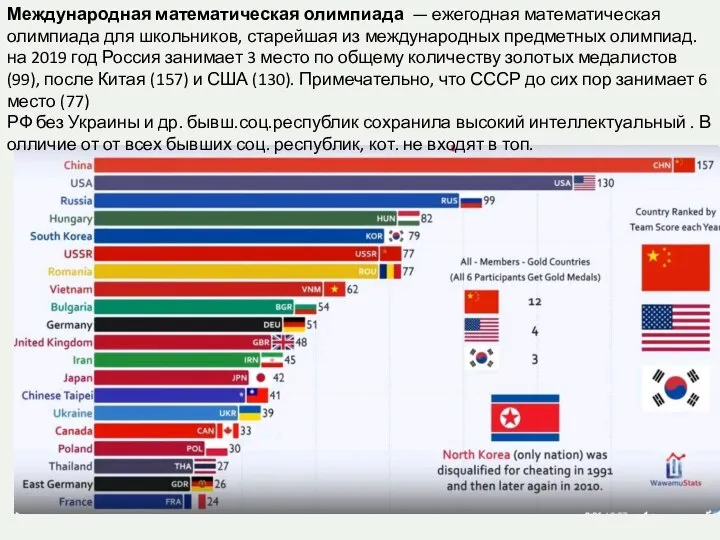 Международная математическая олимпиада
Международная математическая олимпиада Технология квантового обучения в преподавании математики
Технология квантового обучения в преподавании математики Сравнение отрезков и углов геометрических фигур
Сравнение отрезков и углов геометрических фигур Презентация на тему Математический КВН 8 класс
Презентация на тему Математический КВН 8 класс  Условия неопределенности выбора. Ограниченная рациональность
Условия неопределенности выбора. Ограниченная рациональность Векторы. Действия с векторами
Векторы. Действия с векторами Вычитание и сложение чисел
Вычитание и сложение чисел Нумерационные случаи сложения и вычитания чисел второго десятка
Нумерационные случаи сложения и вычитания чисел второго десятка Взаимное расположение графиков линейных функций. 7 класс
Взаимное расположение графиков линейных функций. 7 класс Обработка многократных измерений
Обработка многократных измерений Запомни координаты. Игра
Запомни координаты. Игра Теорема Пифагора для пятиклассников
Теорема Пифагора для пятиклассников Приложения производной
Приложения производной Порядок элемента. Теорема Лагранжа
Порядок элемента. Теорема Лагранжа Теорія множин. Відношення
Теорія множин. Відношення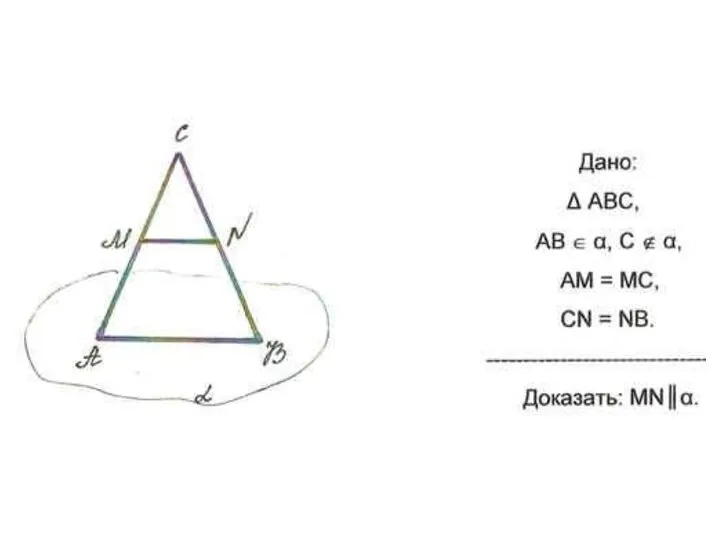 Параллельные прямые. Решение задач
Параллельные прямые. Решение задач урок 1 и 2 (1)
урок 1 и 2 (1) Обеспечивающие подсистемы АИС. Математическое обеспечение
Обеспечивающие подсистемы АИС. Математическое обеспечение Аналоги теореми порівняння Колмогорова та їх застосування
Аналоги теореми порівняння Колмогорова та їх застосування Как можно заменить произведение равных сомножителей?
Как можно заменить произведение равных сомножителей? Многоранники
Многоранники