Бинарные отношения

— Почему ты не пьешь больше чаю? — спросил Заяц заботливо.
— Что значит «больше»? — обиделась Алиса. — Я вообще ничего тут не пила!
— Тем более! — сказал Шляпа. — Выпить больше, чем ничего, — легко и просто.
Вот если бы ты выпила меньше,
чем ничего, это был бы фокус!
Л. Кэрролл

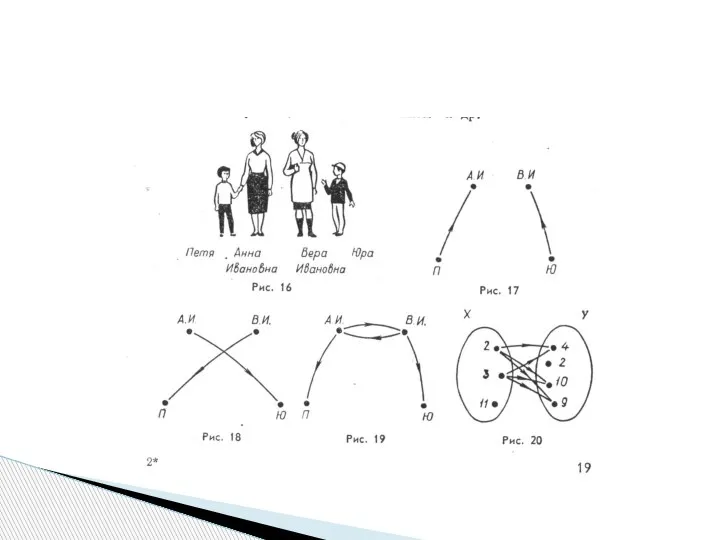
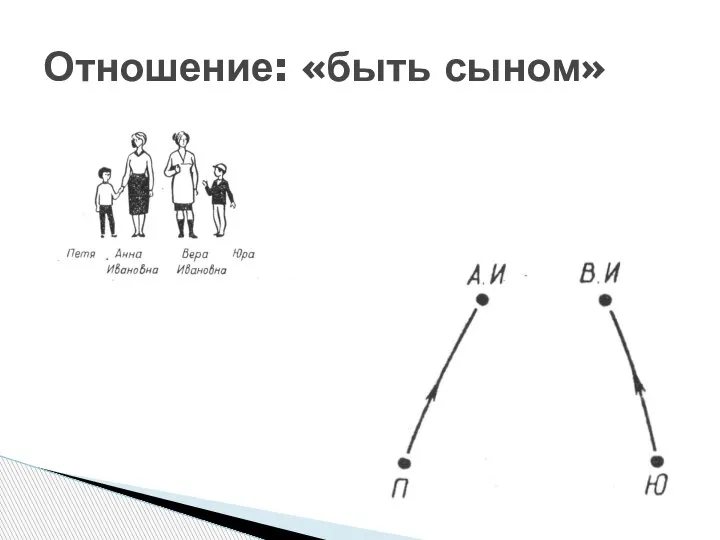
Отношение: «быть сыном»

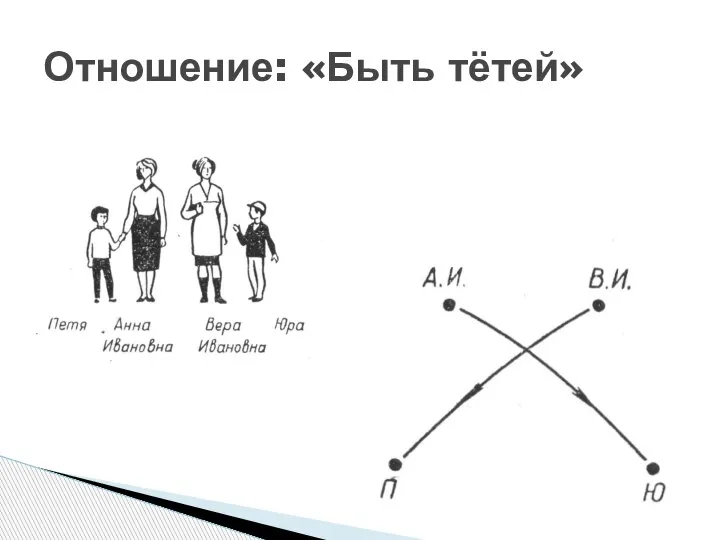
Отношение: «Быть тётей»

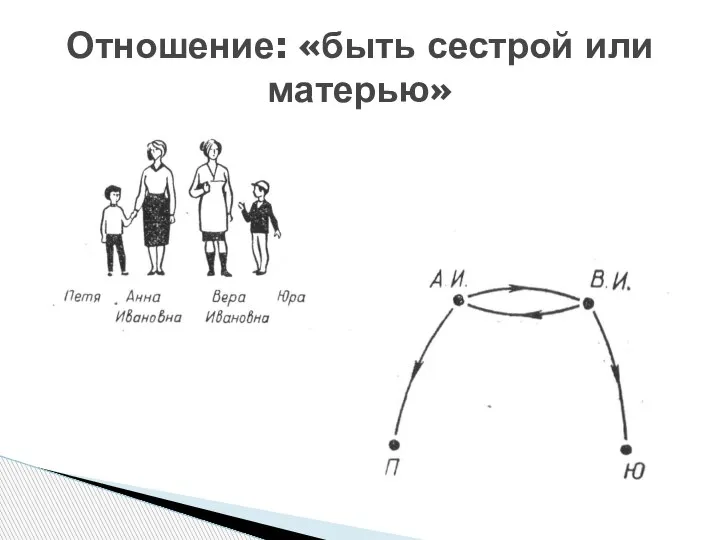
Отношение: «быть сестрой или матерью»

Постройте схемы отношений:
«быть двоюродным братом»
«быть племянником»

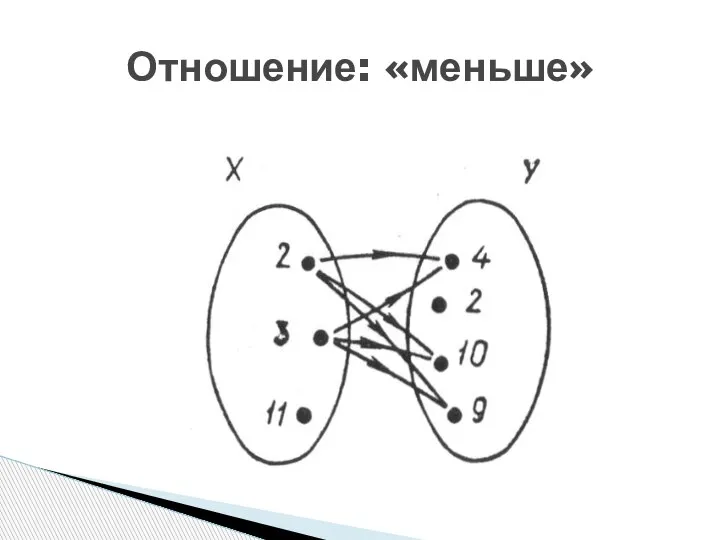
Отношение: «меньше»

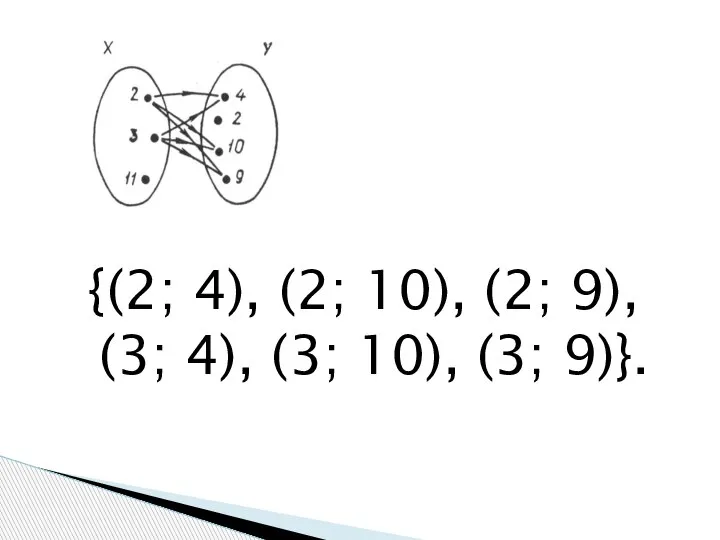
{(2; 4), (2; 10), (2; 9), (3; 4), (3; 10), (3; 9)}.

между элементами двух множеств есть множество пар, которое представляет подмножество декартова произведения множеств.
Отношение

R1 = {(2; 4), (2; 10), (2; 9), (3; 4), (3; 10), (3; 9)}.
Отношение «меньше».

R2 = {(2; 4); (2; 2); (2; 10); (3; 9)}.
Отношение: «быть делителем»

Сколько всего существует отношений между элементами множеств???

Запишите с помощью фигурных скобок все пары элементов, находящихся в отношении «кратно» между элементами множеств
{8; 9; 10; 11} и {4; 5; 8; 11}.

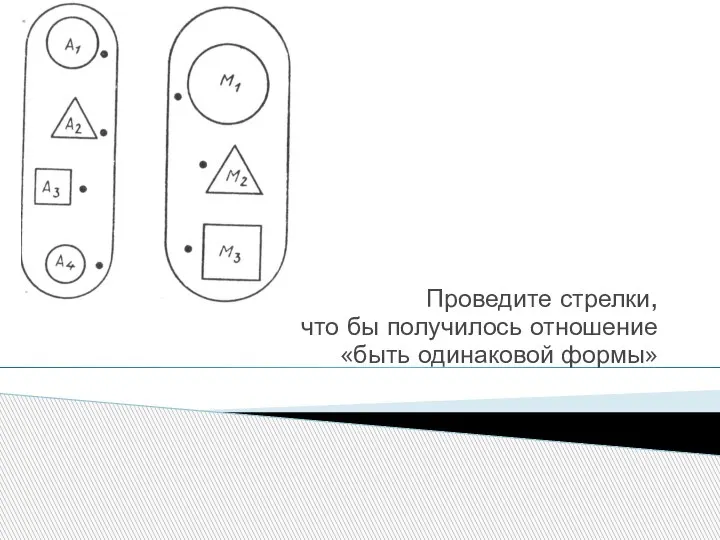
Проведите стрелки,
что бы получилось отношение
«быть одинаковой формы»

а) «больше в 10 раз» между элементами множеств
{30; 50; 70; 90} и {3; 5; 7;9};
б) «меньше на 5» между элементами множеств {0; 5; 11; 9} и {0; 5; 14; 16}.
Начертите граф отношения:

n-местным отношением R на непустом множестве М подмножество R ⊂ Мn
При n = 2 отношение R называется бинарным.
То есть бинарным отношением между элементами множеств А и В называют любое подмножество R множества А×В и записывают R ⊂ А × В.
Для отношения R обратным является отношение R-1 ⊂ В × А.
Определение

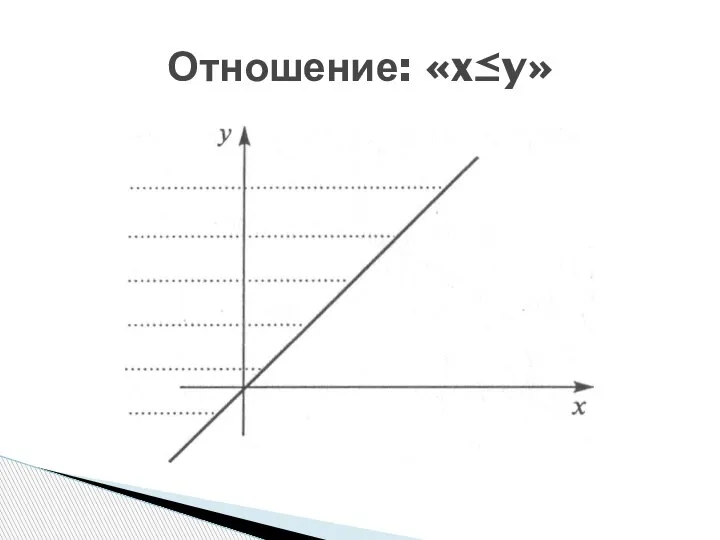
Отношение: «x≤y»

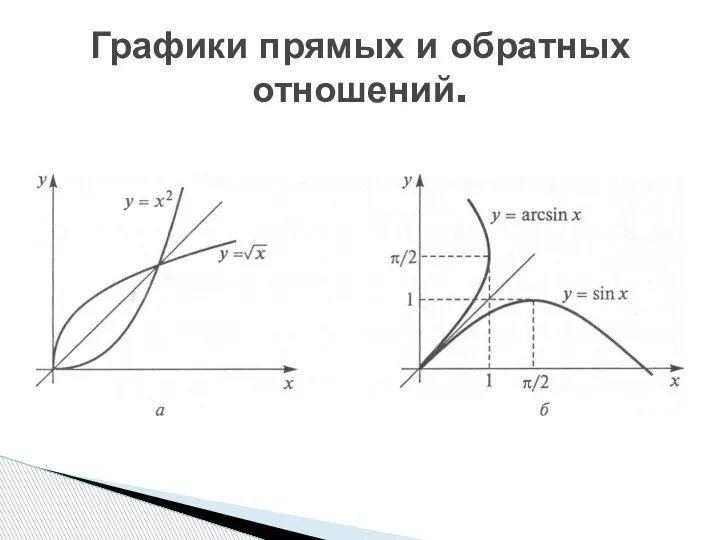
Графики прямых и обратных отношений.

Способы задания бинарных отношений
1. Любое отношение может быть задано в виде списка, элементами которого являются пары, определяемые этим отношением.
Пример.
A={2,3,5,7};
B={24,25,26};
A×B={(2,24),(2,25),(2,26),(3,24),(3,25),(3,26),(5,24),(5,25),
(5,26),(7,24),(7,25),(7,26)}
R⊆A×B
R—“быть делителем”,
R=
{(2,24),(2,26),(3,24),(5,25)}

Способы задания бинарных отношений
2. Бинарное отношение может быть задано с помощью матрицы.
R⊆X×Y
|X|=n, |Y|=m.
n – количество строк,
m – количество столбцов.
Ячейка (i,j) матрицы соответствует паре (xi,yj) элементов, где xi∈X, a yj∈Y.
В ячейку (i,j) помещается 1, если (xi,yj)∈R.
В ячейку (i,j) помещается 0, если (xi,yj)∉R.

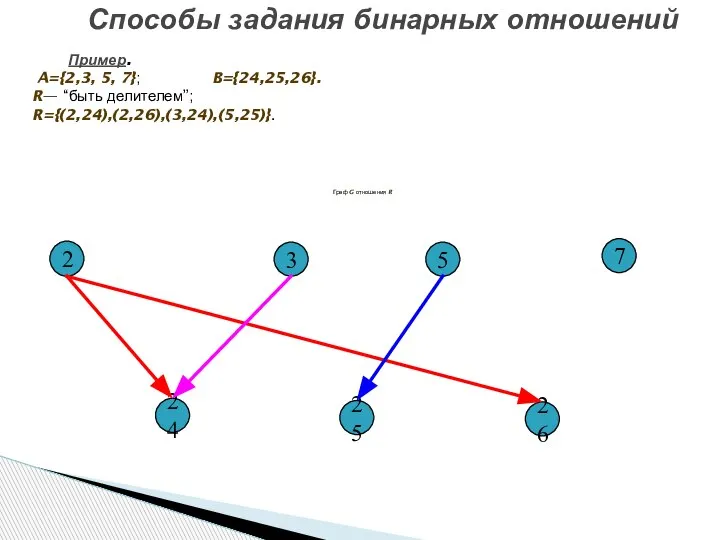
Способы задания бинарных отношений
Пример.
A={2,3,5,7};
B={24,25,26};
R— “быть делителем”
R={(2,24),(2,26),(3,24),(5,25)}
B
A

Способы задания бинарных отношений
3. Бинарное отношение R на множествах X и Y может быть задано графически.
Если пара (xi,yj) принадлежит отношению R, соединяем изображенные точки xi, yj линией, направленной от первого элемента пары ко второму.
Направленные линии, соединяющие пары точек, называются дугами, а точки, обозначающие элементы множеств – вершинами графа.

Способы задания бинарных отношений
Пример.
A={2,3, 5, 7}; B={24,25,26}.
R— “быть делителем”;
R={(2,24),(2,26),(3,24),(5,25)}.
Граф G отношения R
2
3
5
7
24
25
26

Свойства бинарных отношений.

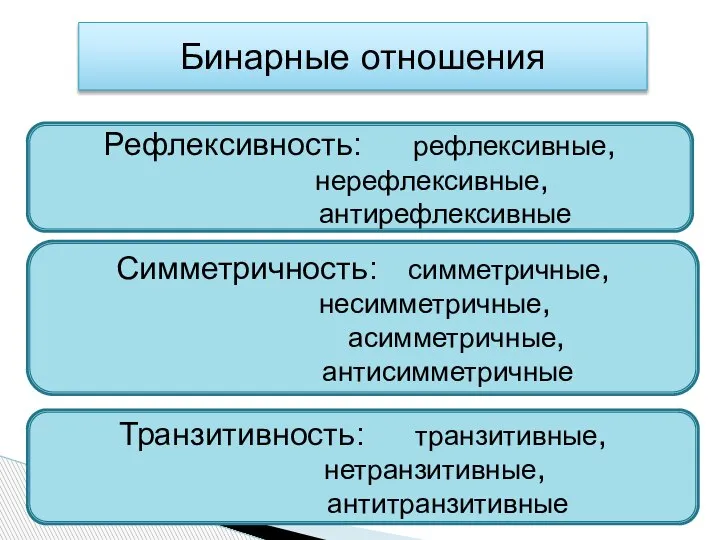
Бинарные отношения
Рефлексивность: рефлексивные,
нерефлексивные,
антирефлексивные
Симметричность: симметричные,
несимметричные,
асимметричные,
антисимметричные
Транзитивность: транзитивные,
нетранзитивные,
антитранзитивные

Рефлексивность
Определение 1. Бинарное отношение R на множестве М называется рефлексивным, если каждый элемент этого множества находится в отношении с самим собой: xRx ∀х ∈ М.
Пример.
1. Отношение сравнимости рефлексивно (при любом натуральном т и на любом множестве целых чисел).
2. Отношение строгого неравенства на множестве вещественных чисел не рефлексивно.
3. Отношение делимости рефлексивно (на любом множестве целых чисел, не содержащем нуля).

Рефлексивность
Определение. Бинарное отношение R на множестве М называется антирефлексивным, если ни один элемент этого множества не находится в отношении с самим собой: ∀х ∈ М неверно, что xRx.
Пример.
1. Отношение строгого неравенства на множестве вещественных чисел антирефлексивно.
2. Отношение взаимной простоты антирефлексивно на любом множестве целых чисел, не содержащем 1 и —1;
рефлексивно на множествах {1},{—1},{—1; 1}
и не является ни рефлексивным, ни антирефлексивным в ином случае.

Рефлективность: aRa.
2. Антирефлективность.
Имеет место, когда отношение не обладает свойством 1 для любых а.

Симметричность
Определение. Бинарное отношение R на множестве М называется симметричным, если вместе с каждой парой (х;у) в отношение входит и симметричная пара (у; х): ∀х,у ∈M xRy = yRx.
Пример.
1. Отношение сравнимости симметрично при любом натуральном т и на любом множестве целых чисел.
2. Отношение строгого неравенства на множестве вещественных чисел не симметрично.
3. Отношение взаимной простоты симметрично на любом множестве целых чисел.

Симметричность
Определение . Бинарное отношение R на множестве М называется асимметричным, если ни одна пара не входит в отношение вместе с симметричной ей: ∀х, у ∈ М, если xRy, то неверно, что yRx.
Пример.
1. Отношение строгого неравенства на множестве вещественных чисел асимметрично.
2. Отношение делимости не является асимметричным ни на каком множестве целых чисел, не содержащем нуля.

Симметричность
Определение. Бинарное отношение R на множестве М называется антисимметричным, если никакая пара, состоящая из разных элементов, не входит в отношение вместе с симметричной ей: ∀х, у ∈ М, если xRy и yRx, то х = у.

3. Симметричность любых двух элементов.
Отношение R на множестве М называется симметричным, если для любых a, b ∈М одновременно справедливо aRb и bRa.
4. Антисимметричность.
Если для несовпадающих элементов а ≠b верно отношение aRb, то ложно bRa.

Симметричность
Определение. Бинарное отношение R на множестве М называется антисимметричным, если никакая пара, состоящая из разных элементов, не входит в отношение вместе с симметричной ей: ∀х, у ∈ М, если xRy и yRx, то х = у.
Пример.
1. Отношение нестрогого неравенства на множестве вещественных чисел антисимметрично.
2. Отношение делимости является антисимметричным на любом множестве целых чисел, не содержащем нуля.

Транзитивность
Определение. Бинарное отношение R на множестве М называется транзитивным, если вместе с парами (х; у) и (у; z) в отношение входит и пара (х, z), т. е. ∀х,у,z ∈ М, если xRy и yRz, то xRz.
Замечание . Свойство транзитивности хорошо иллюстрируется отношением достижимости: если пункт у достижим из пункта х, а из пункт z - из пункта у, то пункт z достижим из пункта х.

Транзитивность
Определение. Бинарное отношение R на множестве М называется транзитивным, если вместе с парами (х; у) и (у; z) в отношение входит и пара (х, z), т. е. ∀х,у,z ∈ М, если xRy и yRz, то xRz.
Пример 1. Отношение сравнимости транзитивно при любом натуральном т и на любом множестве целых чисел.
2. Отношение строгого (нестрогого) неравенства транзитивно на любом подмножестве вещественных чисел.
3. Отношение взаимной простоты не является транзитивным на любом множестве целых чисел. Например, 2 взаимно просто с 3; 3 взаимно просто с 4, но 2 и 4 не взаимно просты.

5. Транзитивность.
Если aRb и bRc, то aRc для любых а, b, с ∈М.
6. Антитранзитивность.
Имеет место, когда отношение не обладает свойством 5.

7. Асимметричность.
Ни для одной пары а и b не выполняется одновременно aRb и bRa.
8. Связность.
Для любых а и Ь, если а ≠b, то aRb или bRa.

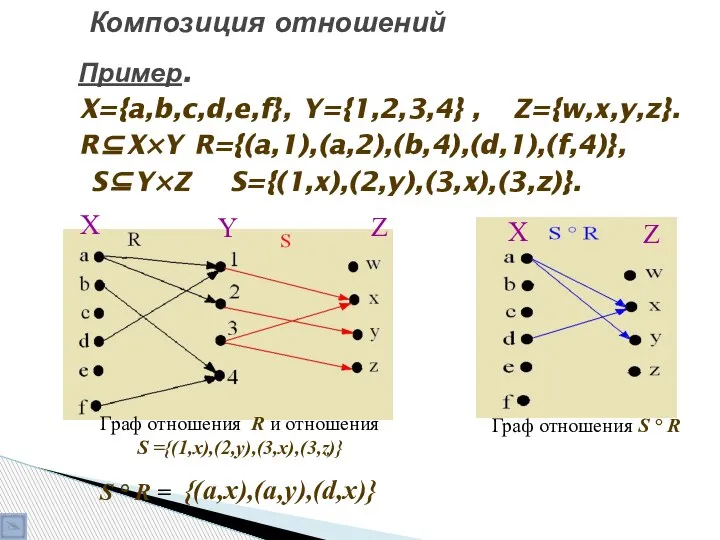
Композиция отношений
Пусть R и S – отношения,
R⊆X×Y, S⊆Y×Z, где X, Y, Z – некоторые множества.
Композицией отношений R и S называется отношение, состоящее из упорядоченных пар (x,z), x∈X, z∈Z, для которых существует элемент y∈Y такой, что выполняются условия (x,y)∈R, (y,z)∈S.
Композиция отношений R и S обозначается S ° R.

Композиция отношений
Пример.
X={a,b,c,d,e,f}, Y={1,2,3,4} , Z={w,x,y,z}.
R⊆X×Y R={(a,1),(a,2),(b,4),(d,1),(f,4)},
S⊆Y×Z S={(1,x),(2,y),(3,x),(3,z)}.
S ° R =
{(a,x),(a,y),(d,x)}
Z
X

Отношение эквивалентности
Бинарное отношение называется отношением эквивалентности (обозначается ~), если оно
1) рефлексивно;
2) симметрично;
3) транзитивно.
Пример.
R1 — “=” на любом множестве.
R2 — “учиться в одной группе” на множестве студентов университета.

Отношение порядка
Бинарное отношение называется отношением частичного порядка (обозначается ≤), если оно
1) рефлексивно;
2) антисимметрично;
3) транзитивно.
Если на множестве задано отношение частичного порядка, то это множество называется частично упорядоченным.
Пример.
R1 — “являться нестрогим включением”, заданное на системе множестве.

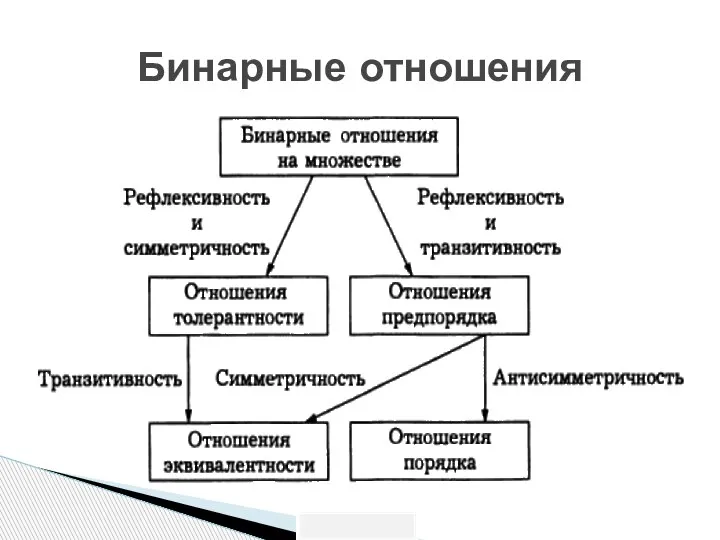
Бинарные отношения

Контрольные вопросы:
Что понимается под соответствием между множествами?
Какое отношение называется бинарным?
Какое бинарное отношение называется рефлексивным? Приведите пример.
Какое бинарное отношение называется антирефлексивным? Приведите пример.
Какое бинарное отношение называется симметричным? Приведите пример.
Какое бинарное отношение называется асимметричным? Приведите пример.
Какое бинарное отношение называется антисимметричным? Приведите пример.
Какое бинарное отношение называется транзитивным? Приведите пример.