Содержание
- 2. Вероятность случайного события Степень объективной возможности случайного события можно измерять числом. Это число называется вероятностью случайного
- 3. Абсолютная и относительная частота
- 4. Статистическое определение вероятности Вероятностью события А в данном испытании называют число P(A), около которого группируются значения
- 5. Полной группой событий называется множество всех событий для данного испытания, если его результатом становится выполнение хотя
- 8. Классическое определение вероятности
- 9. Противоположные события С каждым событием A связано противоположное событие В, состоящее в том, что событие A
- 10. Достоверные события Событие называется достоверным, если оно наступает всегда, при любом испытании. Вероятность достоверного события всегда
- 11. Невозможные события Событие называют невозможным, если оно не наступает никогда, то есть благоприятных исходов для него
- 12. Независимые события Несколько событий А1, А2,…Аk называются независимыми в совокупности, если вероятность появления любого из них
- 13. Сумма событий Суммой событий А и В называют событие С=А+В, состоящее в наступлении хотя бы одного
- 14. Произведение событий Произведением событий А и В называют событие С=АВ, состоящее в том, что в результате
- 15. Теорема сложения вероятностей совместимых событий Вероятность суммы двух совместимых событий А и В равна сумме вероятностей
- 16. Теорема сложения вероятностей несовместимых событий Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий: Р(А+В)=Р(А)+Р(В)
- 17. Теорема умножения вероятностей независимых событий Вероятность произведения двух независимых событий равна произведению вероятностей этих событий Р(АВ)=Р(А)Р(В)
- 18. Условная вероятность Пусть события А и В – зависимые. Условной вероятностью события Р(А /В) называется вероятность
- 19. Теорема умножения вероятностей Вероятность произведения двух событий А и В равна произведению вероятности одного из них
- 20. Вопрос 1 Вероятность наступления некоторого события НЕ МОЖЕТ быть равна: 3/2 1 0 2/3
- 21. Вопрос 2 Среди перечисленных событий достоверным является: выпадение 6 очков при выбрасывании игральной кости выпадение менее
- 22. Вопрос 3 Среди перечисленных событий при однократном бросании игральной кости совместимы Выпадение четного числа очков и
- 23. Вопрос 4 Игральный кубик бросают один раз. Вероятность того, что на грани выпадет число очков большее
- 24. Вопрос 5 При испытании партии приборов относительная частота исправных изделий оказалась равной 0,98. Число неисправных приборов
- 25. В урне 3 белых и 9 черных шаров. Из урны наугад вынимается 1 шар. Какова вероятность
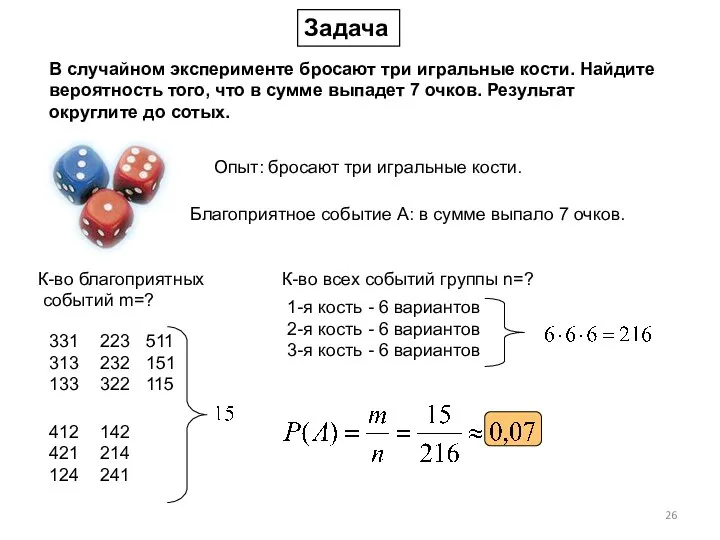
- 26. В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков.
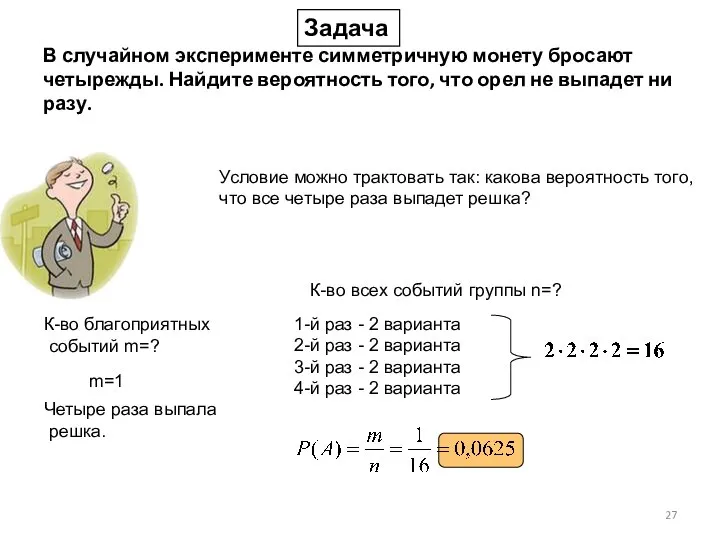
- 27. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орел не выпадет ни разу.
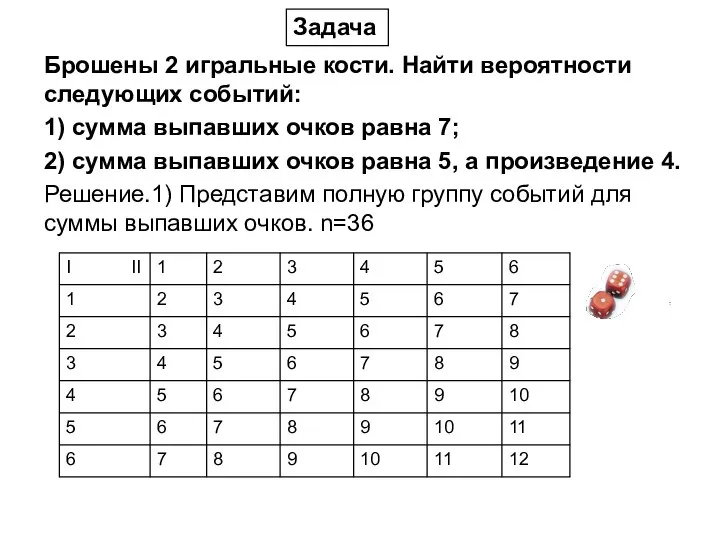
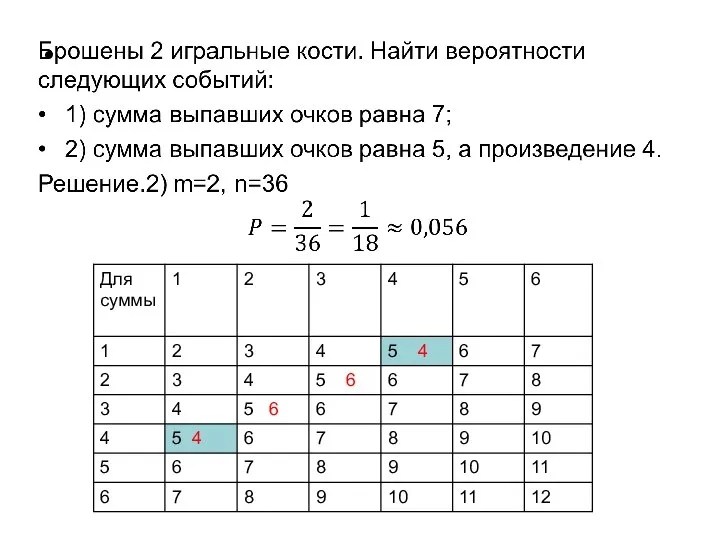
- 28. Брошены 2 игральные кости. Найти вероятности следующих событий: 1) сумма выпавших очков равна 7; 2) сумма
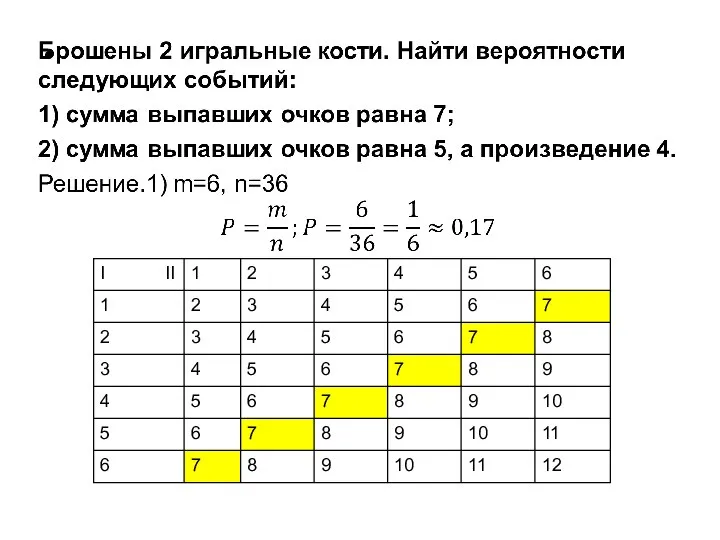
- 29. Брошены 2 игральные кости. Найти вероятности следующих событий: 1) сумма выпавших очков равна 7; 2) сумма
- 33. Ребенок играет с карточками разрезной азбуки с буквами А,А,Е, К,Р, Т. Найти вероятность, что он случайно
- 34. Задача
- 35. Задача
- 36. Стрелок производит один выстрел по мишени. Событие А – 10 очков P(A)=0,11 Событие B – 9
- 37. Стрелок производит один выстрел по мишени. Событие А – 10 очков P(A)=0,11 Событие B – 9
- 38. Задача
- 39. Сигнализация имеет 2 независимых датчика. Вероятность срабатывания 1-го равна 0,95, а второго 0,98. Найти вероятность, что:
- 42. 10 человек собрались в кино. Билеты купили в один ряд, места с 1 по 10 распределили
- 43. m= , n=
- 45. Скачать презентацию





































 Решение задач. Диагностика 1
Решение задач. Диагностика 1 Математический диктант. 6 класс
Математический диктант. 6 класс Числовые ряды
Числовые ряды Соотношение числа и цифры. Считаем от 1 до 9
Соотношение числа и цифры. Считаем от 1 до 9 Обзор мультимедийных дисков по математике 1. Виртуальная школа Кирилла и Мефодия. 2. Серия «Все задачи школьной математики». 3. «Ма
Обзор мультимедийных дисков по математике 1. Виртуальная школа Кирилла и Мефодия. 2. Серия «Все задачи школьной математики». 3. «Ма Повторим правила образования и записи чисел
Повторим правила образования и записи чисел Диофантово уравнение
Диофантово уравнение Векторы
Векторы Задачі_на_наслідки_із_аксіом_стереометрії
Задачі_на_наслідки_із_аксіом_стереометрії Числовые головоломки
Числовые головоломки 6cc84cfba09801fa77f2178065bede8f
6cc84cfba09801fa77f2178065bede8f Методы оптимизации. Ограничения в виде равенств и неравенств
Методы оптимизации. Ограничения в виде равенств и неравенств Наибольший общий делитель (НОД) и наименьшее общее кратное чисел (НОК)
Наибольший общий делитель (НОД) и наименьшее общее кратное чисел (НОК) Лекция. Матрицы.Операции над матрицами.Определители матриц 2 и 3 порядка
Лекция. Матрицы.Операции над матрицами.Определители матриц 2 и 3 порядка Regresní a korelační analýza
Regresní a korelační analýza Предел функции (часть 2)
Предел функции (часть 2)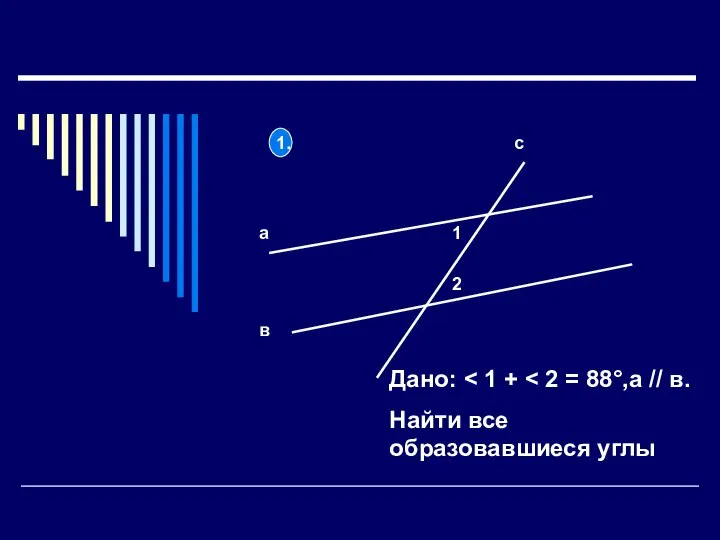 Признаки равенства треугольников
Признаки равенства треугольников Угол между прямой и плоскостью. Теорема о трёх перпендикулярах
Угол между прямой и плоскостью. Теорема о трёх перпендикулярах Подготовка к ЕГЭ (профильный уровень). Задания 5
Подготовка к ЕГЭ (профильный уровень). Задания 5 Уравнения и неравенства в целых числах
Уравнения и неравенства в целых числах Теорема Виета. Устная работа
Теорема Виета. Устная работа Минимизация переключательных функций
Минимизация переключательных функций Прямая и плоскость в пространстве. Лекция 6
Прямая и плоскость в пространстве. Лекция 6 Таблица умножения девяти. Тренажёр-раскраска
Таблица умножения девяти. Тренажёр-раскраска Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда Методика изучения одномерных геометрических фигур в курсе математики начальных классов: точка, линия, прямая
Методика изучения одномерных геометрических фигур в курсе математики начальных классов: точка, линия, прямая Диаграммы Ламерея. Качественный анализ дискретных ДС
Диаграммы Ламерея. Качественный анализ дискретных ДС Сложение десятичных дробей
Сложение десятичных дробей