Логарифмические уравнения

Свойства логарифма

Уравнения, содержащие неизвестное под знаком логарифма или в основании логарифма называются логарифмическими уравнениями.

Решение уравнений, содержащих неизвестное под знаком логарифма, основано на следующих теоремах:

Основные методы решения логарифмических уравнений
По определению логарифма;
Метод потенцирования;
Метод введения новой переменной;
Метод логарифмирования;
Метод приведения к одному основанию;
Функционально-графический метод.

Методы решения логарифмических уравнений
По определению логарифма.
На основе определения логарифма решаются уравнения, в которых по данным основанию и числу определяются логарифм, по данному логарифму и основанию определяется число и по данному числу и логарифму определяется основание.
X=2,5

2. Метод потенцирования.
Под потенцированием понимается переход от равенства, содержащего логарифмы к равенству, не содержащего их.
f(x) = y(x)
Условия для проверки всегда составляем по исходящему уравнению !
при

1
3. Метод введения новой переменной
log22x – 4log2 x + 3=0
log2 x= t, x>0
t2­­­­ – 4t + 3=0
t1=3 t2=1
log2 x=1 log2 x=3
x=2
x=8
Ответ: x=2; 8

4. Метод логарифмирования
x0,5lgx=0,01x2
Прологарифмируем обе части уравнения по основанию 10
lg x 0,5lgx=lg 0,01x2
0,5 lg2x – 2lg x + 2 = 0
t2 – 4t + 4 = 0
t=lg x
0,5t2 – 2t - 2 = 0
(t-2)2 = 0
t = 2 lg x = 2
Ответ: x=100

5. Метод приведения логарифмов к одному и тому же основанию
log9 (37 – 12x) * log7-2x 3 = 1
ОДЗ
0,5log3 (37 - 12x) = log3 (7 – 2x)
log3 (37 - 12x) = log3 (7 – 2x)2
37 – 12x = (7 – 2x)2
37 – 12x = 49 -28x + 4x2
X2 – 4x + 3 = 0
x1­ = 1
x2 = 3 – посторонний корень
Ответ: х = 1

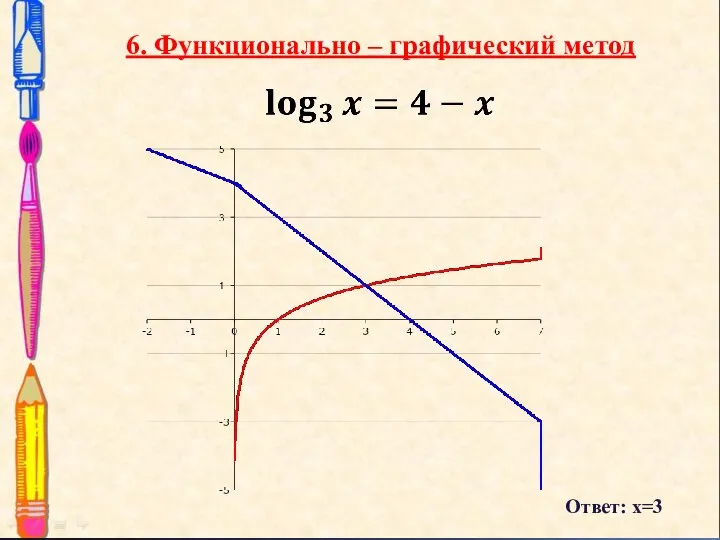
6. Функционально – графический метод
Ответ: х=3

Для решения ЛУ графическим методом надо построить в одной и той же системе координат графики функций, стоящих в левой и правой частях уравнения и найти абсциссу их точки пересечения
Найти корни уравнения
Так как функция у= log3 х возрастающая, а функция у =4-х убывающая на (0; + ∞ ),то заданное уравнение на этом интервале имеет один корень.

7. Использование свойств монотонности функции
log3 x = 11 – x
Так как функции y = log3 x возрастает, а у = 11 – x убывает на (0;+∞),
то уравнение имеет единственное решение, которое можно найти методом подбора: х = 9

Самостоятельная работа (в парах)
Укажите метод и решите уравнения:
Ответы (самопроверка)
15
0,25; 16
2; -4
0, 125; 2
5
125; 0,04
-4
3; 27