Слайд 2Как помочь учащимся легче воспринимать новый материал, как сделать, чтобы они меньше

совершали ошибок? Задумываясь над этим, поняла, что только тогда, когда учитель знает трудности учеников, проблему можно решить.
Слайд 3При изучении ряда тем программы требуется сформировать навыки, которые для учащихся являются

сложными и требуют от них, в свою очередь, овладения не которыми вспомогательными навыками. Так, например, для того чтобы научиться пользоваться формулой квадрата суммы двух слагаемых, учащиеся должны научиться находит сами слагаемые, их квадраты, их произведение и удвоенное произведение.
Опыт показывает, что одновременно и вспомогательными данными, и основным навыком не всем учащимся оказывается под силу.
Слайд 4В своей работе пользуюсь следующим методом. Примерно за две недели до изучения

нового материала начинаю на устных упражнениях готовить ребят к восприятию его. Так при изучении упомянутой выше формулы квадрата суммы двух слагаемых система упражнений следующая. Показываю ученикам сумму ( а + 3 ), прошу назвать первое слагаемое, второе слагаемое; показываю ( в – 5 ) – задание аналогичное.
Слайд 5На следующем уроке выписываю на доске столбик из 10 различных сумм, прошу

назвать слагаемые, квадрат первого слагаемого, квадрат второго слагаемого. Смотрим с учащимися и убеждаемся еще раз, что квадраты любых чисел положительны. На следующих уроках закрепляю умение находить слагаемые, их квадраты, произведение первого и второго слагаемого. Задания чередуются и даются выборочно для написанных заранее на доске сумм, учитель только показывает сумму и сообщает задание.( Это может делать и сильный ученик.)
Слайд 6Далее ввожу понятие удвоенного произведения слагаемых. В итоге после вывода формулы
(

а + b ) 2= а2 + 2аb + b2
ребята оказываются способны находить результат сразу ( например
( 2а + 3 )2 = 4а2 + 12 а + 9,
а не
( 2а )2 + 2·2а ·3 + 32 )
не делают ошибок в знаках, не забывают просчитывать 2аb.
Слайд 7Предварительные упражнения хорошо помогают восприятию формулы корней квадратного уравнения. Использую такую систем:
Выписываю

различные квадратные трехчлены и поясняю что есть а, что – b , что – с. Затем ученики находят а, в, с для нескольких трехчленов. На первых уроках только называем коэффициенты ( выписываю по 10 различных трехчленов ).
Называем а, b, с и вычисляем в ( на одном уроке ).
Вычисляем в2 и ас. Это делаем на одном уроке.
Слайд 8На другом уроке прошу найти b/2 и (b/2)2- учитель только указывает один

из выписанных заранее трехчленов, у которых b четное число. В дальнейшем ученики сами выбирают, что возводить в квадрат b или (b/2). Учитель указывает только один из выписанных заранее трехчленов.
Вычисляем 4ас, а также повторяем вычисления b2 , ( b/2 )2.
Находим значение (b2 – 4ас) или (b/2)2- ас ( дети приучаются выбирать, что именно).
Слайд 9Упражняемся на трех – четырех уроках. К моменту вывода корней квадратного
трехчлена

почти у всех учеников оказывается сформированным навык нахождения
Такие упражнения, проводимые в устном счете, мобилизуют ребят, они кажутся простыми и являются доступными для всех.








 Практико-ориентированные задачи по математике про шины
Практико-ориентированные задачи по математике про шины Статистические характеристики: среднее арифметическое, мода, медиана называются средними результатами измерений
Статистические характеристики: среднее арифметическое, мода, медиана называются средними результатами измерений Обучение для выполнения НИР 5 курса. Занятие №2
Обучение для выполнения НИР 5 курса. Занятие №2 Отношение чисел
Отношение чисел Обыкновенные дифференциальные уравнения
Обыкновенные дифференциальные уравнения Применение интегральной технологии при изучении алгебраических уравнений
Применение интегральной технологии при изучении алгебраических уравнений Рівняння. Видатні українські математики
Рівняння. Видатні українські математики Формулы приведения
Формулы приведения Моделирование – способ, процесс замещения оригинала его аналогом (моделью)
Моделирование – способ, процесс замещения оригинала его аналогом (моделью) Вариационная форма
Вариационная форма Презентация на тему История возникновения геометрии
Презентация на тему История возникновения геометрии  Интерактивный плакат Треугольник
Интерактивный плакат Треугольник Системы уравнений и методы их решения
Системы уравнений и методы их решения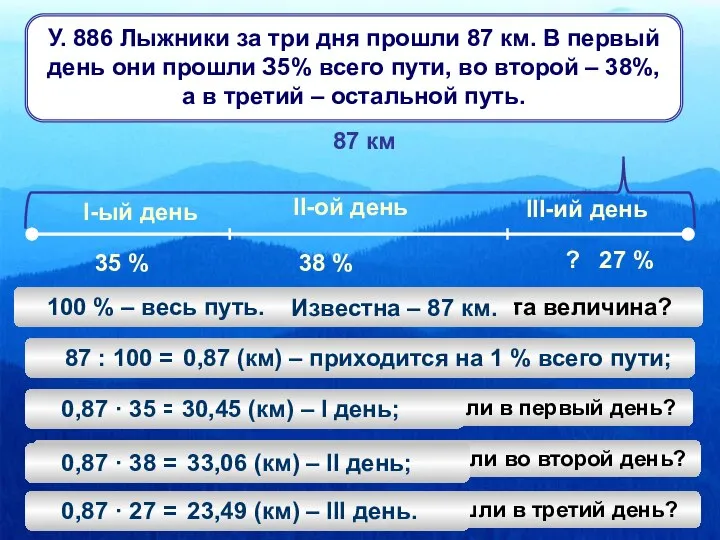 Задачи о лыжниках
Задачи о лыжниках Золотое сечение - красота и гармония в математических расчетах
Золотое сечение - красота и гармония в математических расчетах Презентация на тему Действия с векторами
Презентация на тему Действия с векторами  Сложение чисел. Как можно найти значение суммы 7 + 7
Сложение чисел. Как можно найти значение суммы 7 + 7 Подготовка к ЕГЭ по математике. Задание 16 (задачи по планиметрии)
Подготовка к ЕГЭ по математике. Задание 16 (задачи по планиметрии) Сложение и вычитание десятичных дробей. 18 февраля в истории Кубани
Сложение и вычитание десятичных дробей. 18 февраля в истории Кубани Числовой луч (1 класс)
Числовой луч (1 класс) Онға дейінгі сандармен әрекеттер
Онға дейінгі сандармен әрекеттер Арифметический квадратный корень. Самостоятельная работа
Арифметический квадратный корень. Самостоятельная работа Предел числовой последовательности
Предел числовой последовательности Признаки параллельности прямых
Признаки параллельности прямых Шкала отношений
Шкала отношений Презентация на тему Решение планиметрических задач на нахождение площади фигуры
Презентация на тему Решение планиметрических задач на нахождение площади фигуры  Альтернативные издержки и кривая производственных возможностей
Альтернативные издержки и кривая производственных возможностей Функция одной переменной. Предел функции в точке и непрерывность функции. Точки разрыва. (Лекция 2)
Функция одной переменной. Предел функции в точке и непрерывность функции. Точки разрыва. (Лекция 2)