Содержание
- 2. 6. ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ 6.1 Теоремы о дифференцируемых функциях 6.2 Исследование функции и построение её графика 6.3
- 3. 6. ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ 6.2 Исследование функции и построение её графика 6.2.1 Возрастание и убывание функции 6.2.2
- 4. 6.2.1 ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИИ то функция называется возрастающей. Если Пусть функция y = f(x) определена
- 5. Пусть функция y = f(x) дифференцируема на отрезке [a; b]. Тогда: f(x) – возрастающая f(x) –
- 6. Пусть функция y = f(x) дифференцируема на отрезке [a; b]. Тогда: f(x) – возрастающая, f(x) –
- 7. а) если то это интервал возрастания, б) если то это интервал убывания. 1) Найти область определения
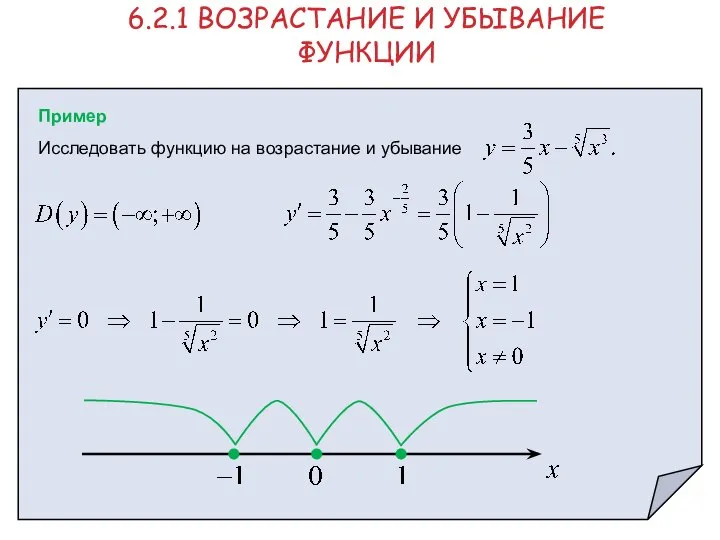
- 8. 6.2.1 ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИИ Пример Исследовать функцию на возрастание и убывание
- 9. 6.2.1 ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИИ Пример Функция возрастает при Функция убывает при
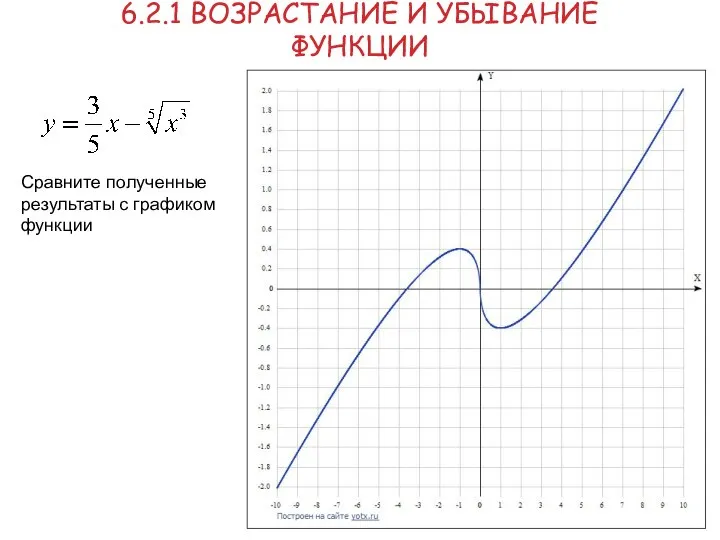
- 10. 6.2.1 ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИИ Сравните полученные результаты с графиком функции
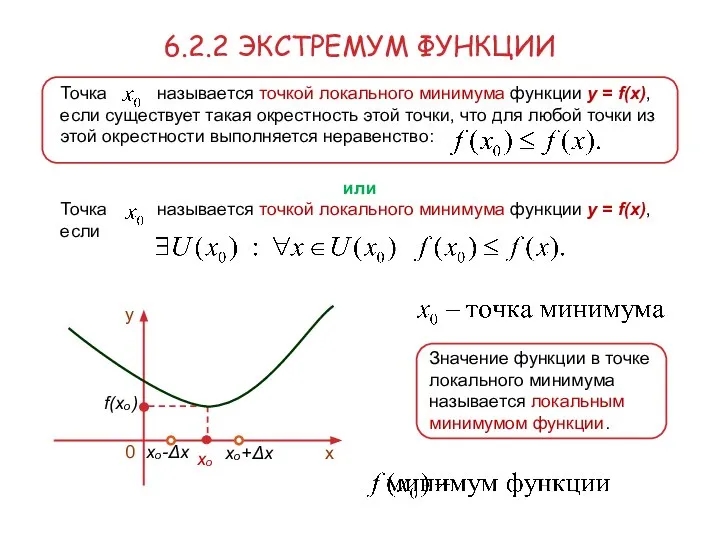
- 11. Точка называется точкой локального максимума функции y = f(x), если существует такая окрестность этой точки, что
- 12. Точка называется точкой локального минимума функции y = f(x), если существует такая окрестность этой точки, что
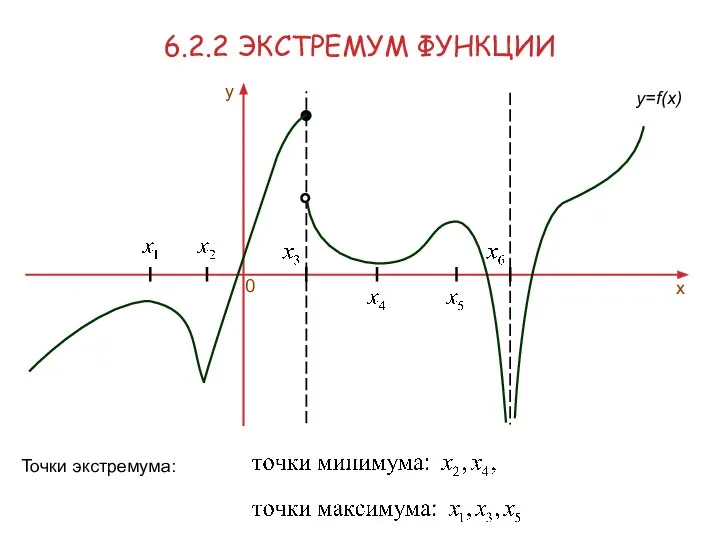
- 13. 6.2.2 ЭКСТРЕМУМ ФУНКЦИИ Точки экстремума:
- 14. Значение функции в точке локального максимума называется локальным максимумом функции. 6.2.2 ЭКСТРЕМУМ ФУНКЦИИ Значение функции в
- 15. Если функция y = f(x) дифференцируема в некоторой точке и имеет в ней экстремум, то производная
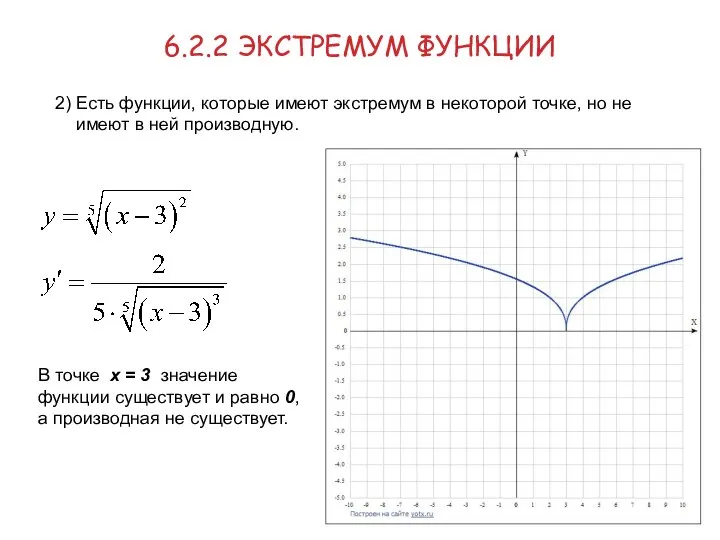
- 16. 6.2.2 ЭКСТРЕМУМ ФУНКЦИИ 2) Есть функции, которые имеют экстремум в некоторой точке, но не имеют в
- 17. Пусть функция y = f(x) непрерывна в некоторой окрестности точки хₒ и дифференцируема в ней, за
- 18. Пусть функция y = f(x) дважды непрерывно дифференцируема в некоторой окрестности точки хₒ, пусть f′ (xₒ)
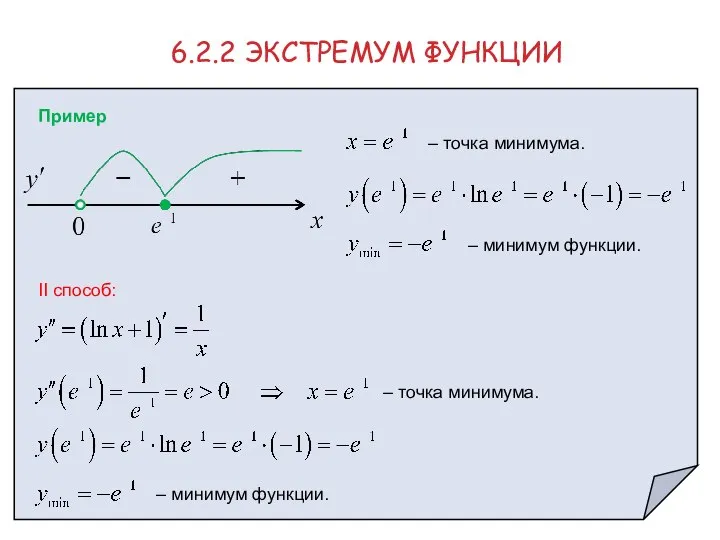
- 19. 6.2.2 ЭКСТРЕМУМ ФУНКЦИИ Пример Исследовать функцию на экстремум I способ:
- 20. 6.2.2 ЭКСТРЕМУМ ФУНКЦИИ Пример II способ: – точка минимума. – минимум функции. – точка минимума. –
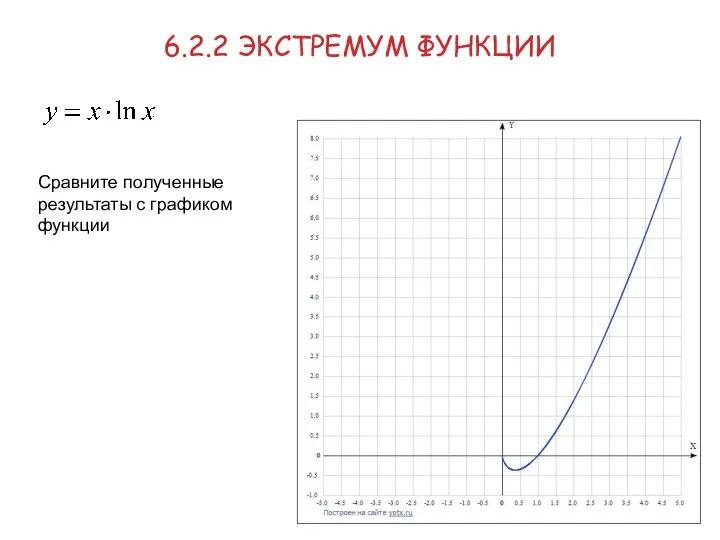
- 21. 6.2.2 ЭКСТРЕМУМ ФУНКЦИИ Сравните полученные результаты с графиком функции
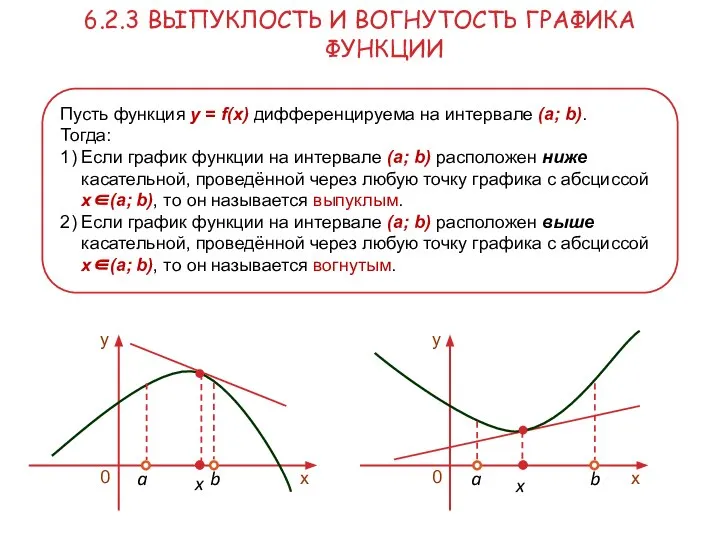
- 22. 6.2.3 ВЫПУКЛОСТЬ И ВОГНУТОСТЬ ГРАФИКА ФУНКЦИИ Пусть функция y = f(x) дифференцируема на интервале (a; b).
- 23. Пусть функция y = f(x) дважды непрерывно дифференцируема на интервале (a; b). Тогда для любой точки
- 24. Пусть функция y = f(x) дважды непрерывно дифференцируема в точке xₒ. Пусть точка М(xₒ; f(xₒ)) есть
- 25. Пусть функция y = f(x) непрерывна в некоторой окрестности критической точки 2-го рода хₒ и дважды
- 26. 1) Найти область определения функции y = f(x). 2) Найти производную второго порядка функции. 3) Найти
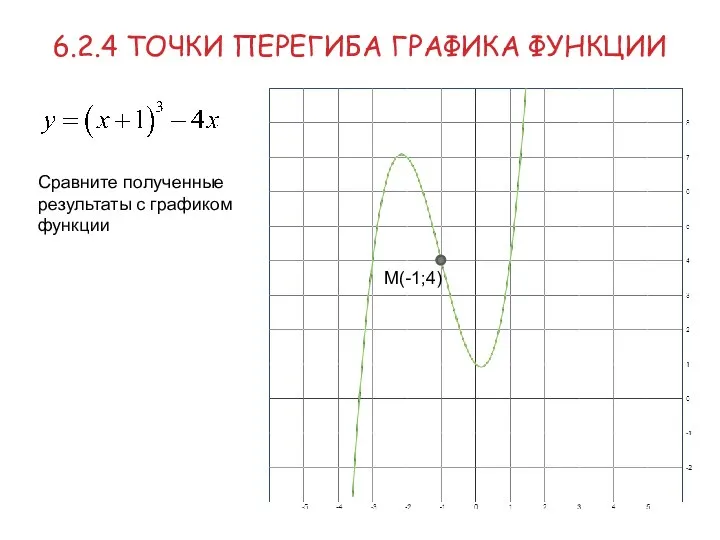
- 27. 6.2.4 ТОЧКИ ПЕРЕГИБА ГРАФИКА ФУНКЦИИ Пример Исследовать функцию на выпуклость и вогнутость, найти точки перегиба График
- 28. 6.2.4 ТОЧКИ ПЕРЕГИБА ГРАФИКА ФУНКЦИИ М(-1;4) Сравните полученные результаты с графиком функции
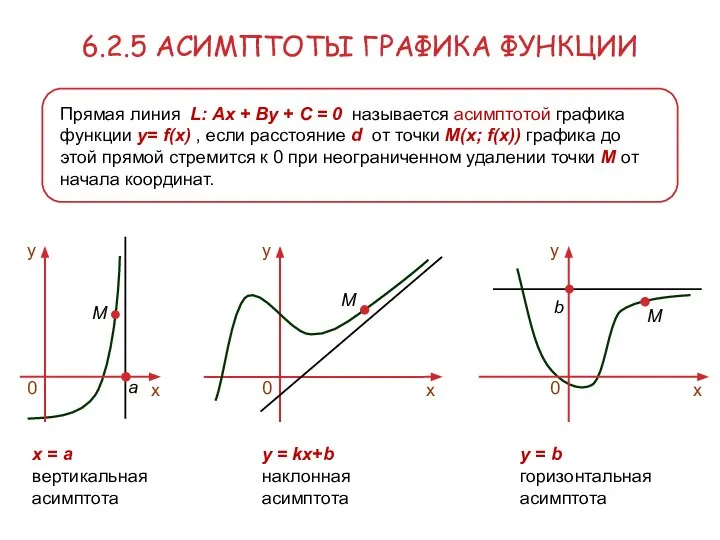
- 29. 6.2.5 АСИМПТОТЫ ГРАФИКА ФУНКЦИИ x = a вертикальная асимптота Прямая линия L: Ax + By +
- 30. Прямая L: x = a является вертикальной асимптотой графика функции y = f(x) тогда и только
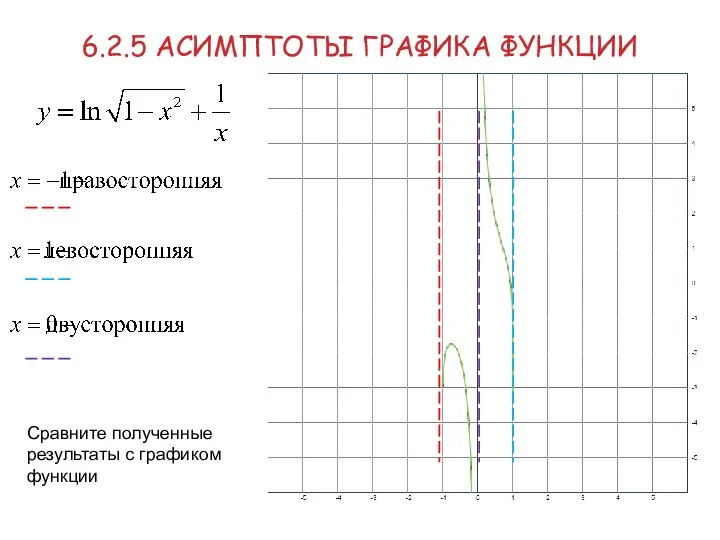
- 31. 6.2.5 АСИМПТОТЫ ГРАФИКА ФУНКЦИИ Пример Найти вертикальные асимптоты графика функции Найдём область определения: Исследуем функцию на
- 32. 6.2.5 АСИМПТОТЫ ГРАФИКА ФУНКЦИИ Пример Значит, х = 0 – точка разрыва 2-го рода. Получили: х
- 33. 6.2.5 АСИМПТОТЫ ГРАФИКА ФУНКЦИИ Сравните полученные результаты с графиком функции
- 34. Прямая L: y = kx+b является наклонной асимптотой графика функции y = f(x) тогда и только
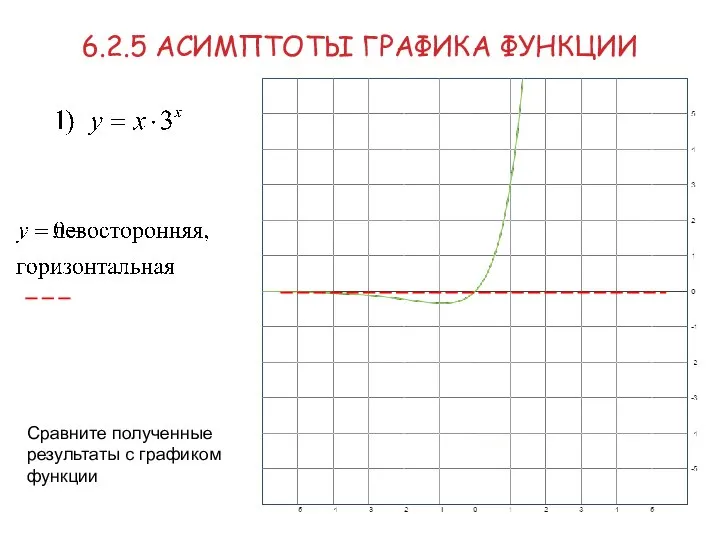
- 35. 6.2.5 АСИМПТОТЫ ГРАФИКА ФУНКЦИИ Примеры Найти асимптоты графика функции: вертикальных асимптот нет. Найдём наклонные асимптоты (сначала
- 36. 6.2.5 АСИМПТОТЫ ГРАФИКА ФУНКЦИИ Сравните полученные результаты с графиком функции
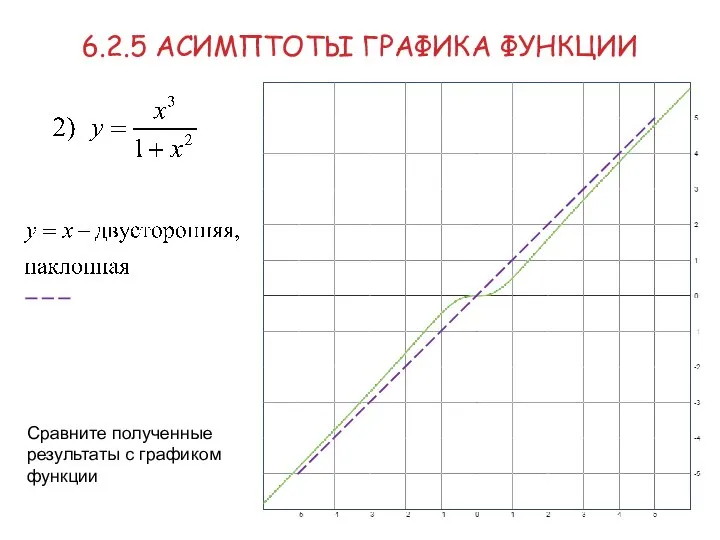
- 37. 6.2.5 АСИМПТОТЫ ГРАФИКА ФУНКЦИИ Примеры Найти асимптоты графика функции: вертикальных асимптот нет. Найдём наклонные асимптоты (для
- 38. 6.2.5 АСИМПТОТЫ ГРАФИКА ФУНКЦИИ Сравните полученные результаты с графиком функции
- 39. 1) Найти область определения функции y = f(x). 2) Исследовать функцию на непрерывность, найти точки разрыва
- 41. Скачать презентацию



![Пусть функция y = f(x) дифференцируема на отрезке [a; b]. Тогда: f(x)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1049410/slide-4.jpg)
![Пусть функция y = f(x) дифференцируема на отрезке [a; b]. Тогда: f(x)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1049410/slide-5.jpg)




















 قدرمطلقی درجه اول
قدرمطلقی درجه اول Способы решения показательных уравнений
Способы решения показательных уравнений Преобразования графиков
Преобразования графиков Математика. 3 класс
Математика. 3 класс Презентация на тему Страна отрицательных чисел
Презентация на тему Страна отрицательных чисел  Презентация на тему Угол вписанный в окружность
Презентация на тему Угол вписанный в окружность  Великолепная пятерка. Математический калейдоскоп
Великолепная пятерка. Математический калейдоскоп Обобщающий урок по начертательной геометрии прямая. Плоскость
Обобщающий урок по начертательной геометрии прямая. Плоскость Раскрытие скобок
Раскрытие скобок Планиметрия. Четырёхугольники
Планиметрия. Четырёхугольники Решение по готовы чертежам по теме: Длина окружности, 9 класс
Решение по готовы чертежам по теме: Длина окружности, 9 класс Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями Матричный способ решения СЛАУ и метод Крамера
Матричный способ решения СЛАУ и метод Крамера Рациональные приемы вычислений
Рациональные приемы вычислений Подготовка к ВПР. Равенство
Подготовка к ВПР. Равенство pril1
pril1 Шкала. Координатный луч
Шкала. Координатный луч Степенные ряды
Степенные ряды Числовые промежутки
Числовые промежутки Prezentado de enspezoj
Prezentado de enspezoj Сравнение чисел. 1 класс
Сравнение чисел. 1 класс Раскрытие скобок
Раскрытие скобок Математика 1 класс. УМК Перспектива. Урок 1. Форма предметов
Математика 1 класс. УМК Перспектива. Урок 1. Форма предметов Построение информационной модели метода изготовления изделия
Построение информационной модели метода изготовления изделия Геометрические построения
Геометрические построения Числовая окружность на координатной плоскости
Числовая окружность на координатной плоскости ЕГЭ 2021. Задания 1-19 (11 класс)
ЕГЭ 2021. Задания 1-19 (11 класс) Метрология
Метрология