Содержание
- 2. План вебинара Разбор ДЗ – ключевые моменты. Функция и отображения. Вычисление пределов: + рациональных функций; +
- 3. Задача 2 (1) Исходное (ложь; sgn(0)=0): Отрицание (истина):
- 4. (2) Исходное (-; теорема Ферма): Отрицание (+):
- 5. (3) Исходное (+): Отрицание:
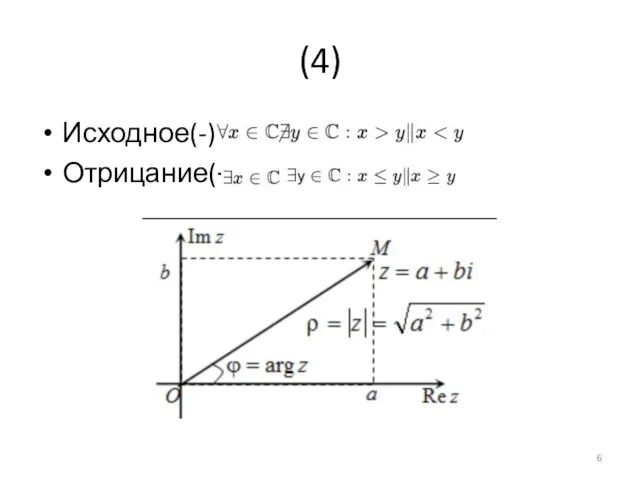
- 6. (4) Исходное(-): Отрицание(+):
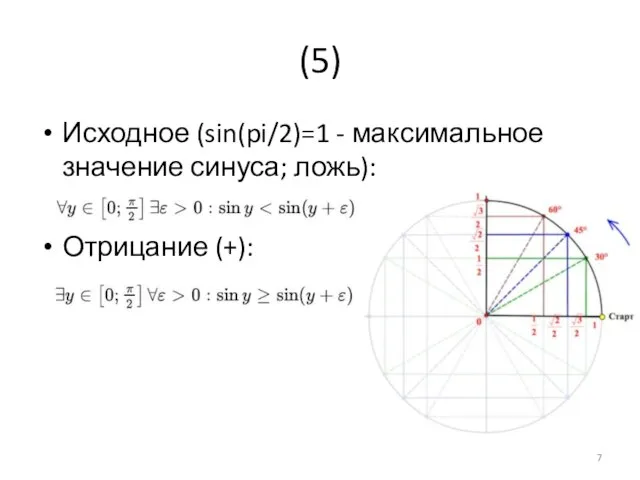
- 7. (5) Исходное (sin(pi/2)=1 - максимальное значение синуса; ложь): Отрицание (+):
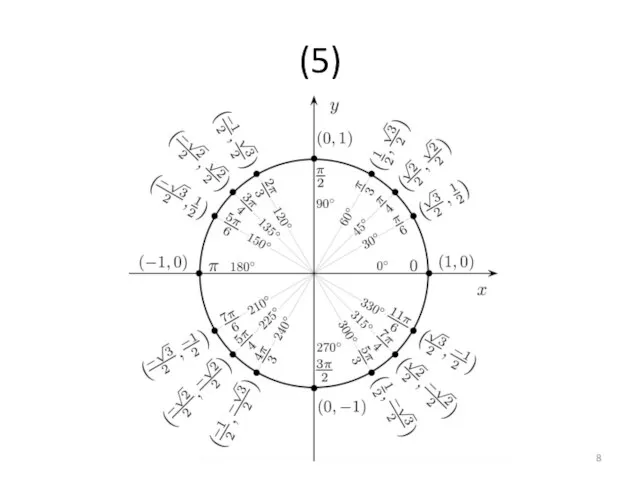
- 8. (5)
- 9. (6) Исходное (+): Отрицание: Принадлежность множеству не меняется. ε в обоих случаях положительно.
- 10. (7) Исходное (+): Отрицание:
- 11. Множества, №1
- 12. Формула Стирлинга (к следующему дз)
- 13. ГРАФИК – для иллюстрации Число е: https://ru.wikipedia.org/wiki/E_(%D1%87%D0%B8%D1%81%D0%BB%D0%BE)
- 14. Полезные формулы (напоминание) x1, x2 – корни уравнения ax 2 + bx+ c = 0 Формулы
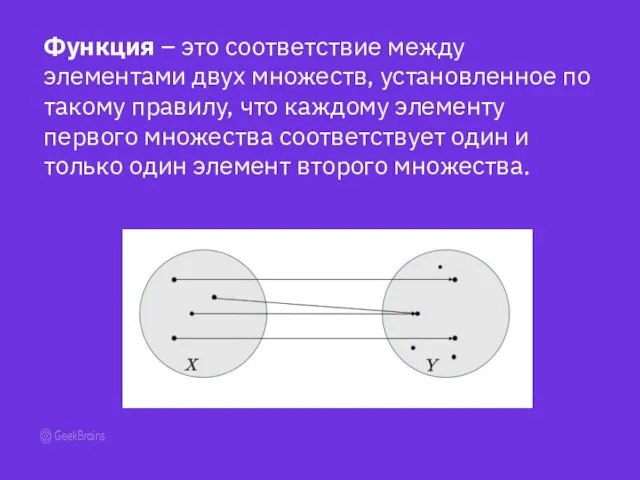
- 16. Функция – это соответствие между элементами двух множеств, установленное по такому правилу, что каждому элементу первого
- 17. Виды отображений: сюрьекция Отображение называется сюръекцией, если каждый элемент множества Y является образом хотя бы одного
- 18. Виды отображений: инъекция Отображение называется инъекцией, если разные элементы множества Х переводятся в разные элементы множества
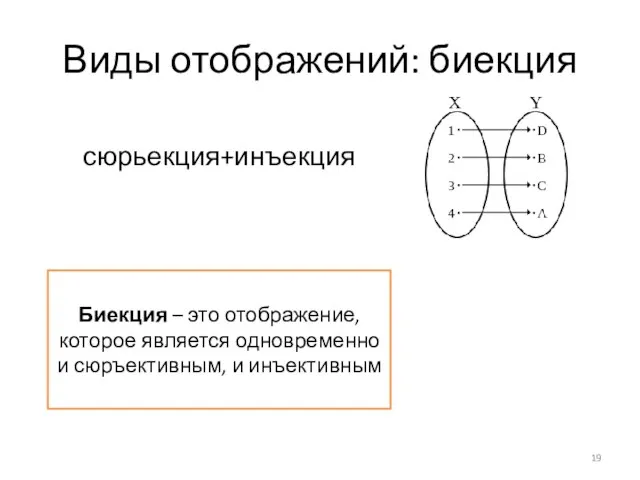
- 19. Виды отображений: биекция Биекция – это отображение, которое является одновременно и сюръективным, и инъективным сюрьекция+инъекция
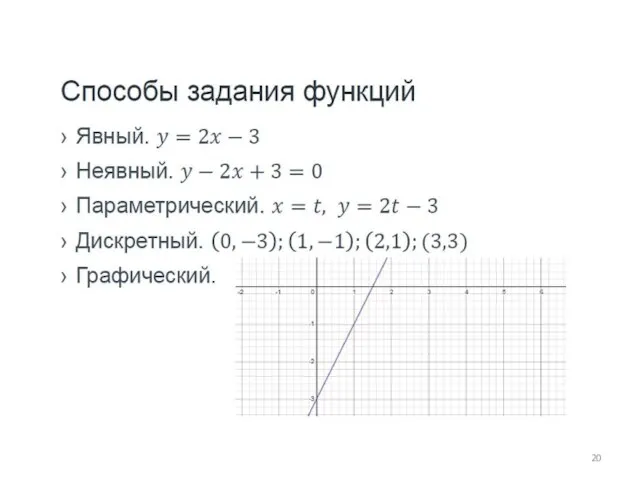
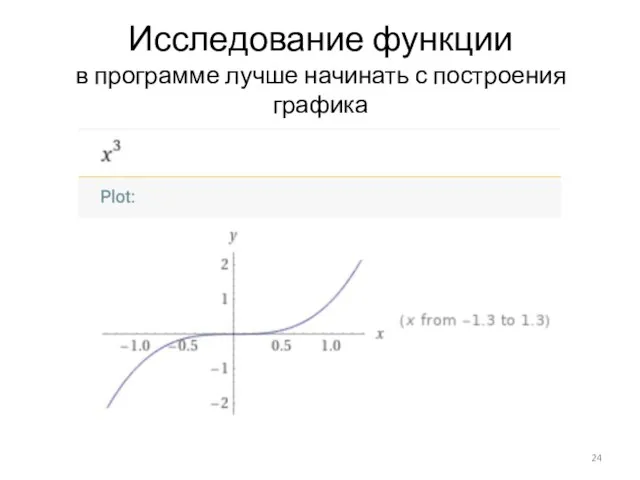
- 21. Исследование функции в программе лучше начинать с построения графика Область определения — множество, на котором задаётся
- 22. Исследование функции в программе лучше начинать с построения графика 4) Отрезки знакопостоянства: f(x)>0; f(x) 5) Чётность
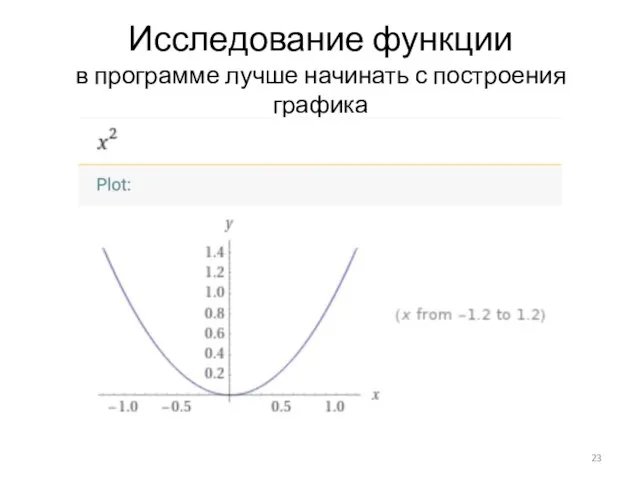
- 23. Исследование функции в программе лучше начинать с построения графика
- 24. Исследование функции в программе лучше начинать с построения графика
- 25. Исследование функции в программе лучше начинать с построения графика 6) Ограниченность функции: есть ли максимальное и
- 26. Нахождение предела функции: начало Подставляем в функцию значение, к которому стремится «икс»; Устанавливаем вид неопределённости.
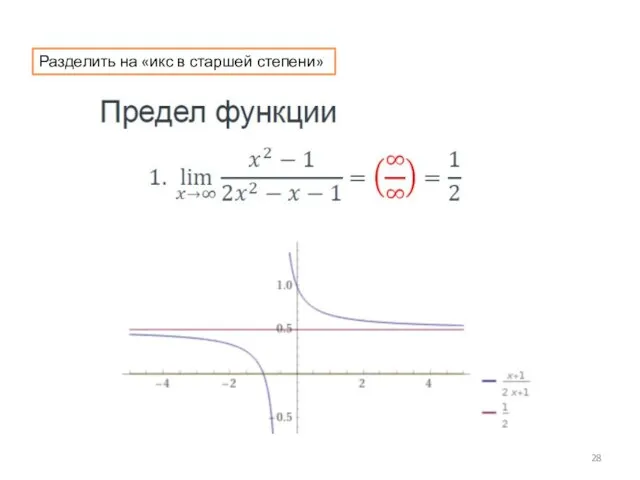
- 28. Разделить на «икс в старшей степени»
- 29. Разделить на «икс в старшей степени»
- 32. Разложить на множители
- 33. Разложить на множители ax^2+bx+c=0 x1, x2 – корни, Тогда ax^2+bx+c = a(x-x1)(x-x2)
- 35. Разделить на «икс в старшей степени»
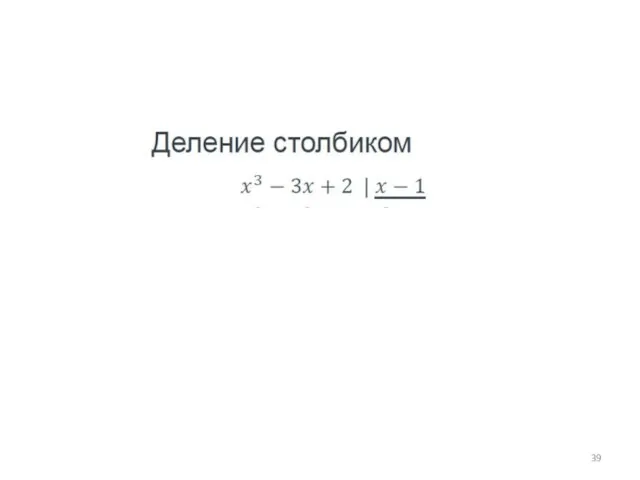
- 38. Разложить на множители ax 2 + bx+ c = a ( x – x1 ) (
- 46. Умножить на сопряжённый множитель
- 63. Эквивалентности в пределах
- 64. Продолжение следует…
- 66. Скачать презентацию
















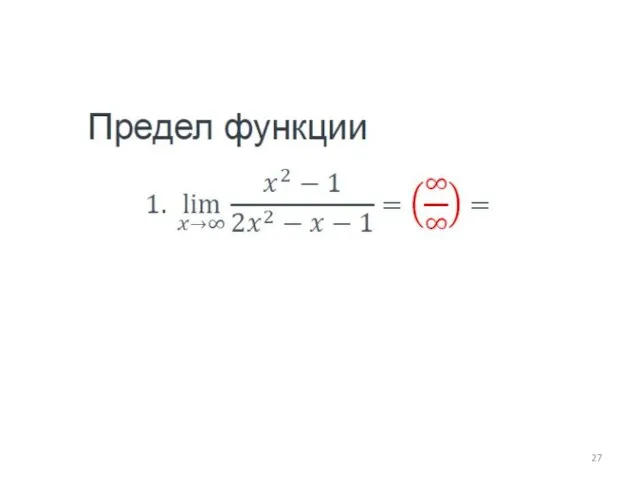























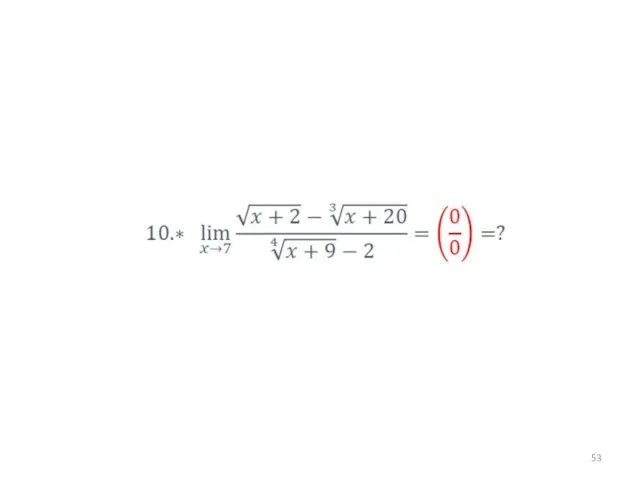











 Презентация на тему Формулы сокращённого умножения
Презентация на тему Формулы сокращённого умножения  тринометрические функции
тринометрические функции Деление одночлена на одночлен
Деление одночлена на одночлен Теоремы сложения и умножения вероятностей
Теоремы сложения и умножения вероятностей Двоичная арифметика
Двоичная арифметика Презентация на тему Умножение суммы на число
Презентация на тему Умножение суммы на число  Обучение решению задач на движение при обобщающем повторении
Обучение решению задач на движение при обобщающем повторении Обчислення площі прямокутника, розв'язування задач, пов'язаних із площею прямокутника. 4 клас
Обчислення площі прямокутника, розв'язування задач, пов'язаних із площею прямокутника. 4 клас Область визначення функції
Область визначення функції Презентация на тему Тренажер по формулам сокращенного умножения
Презентация на тему Тренажер по формулам сокращенного умножения  Презентация на тему ПРОИЗВОДНАЯ СТЕПЕННОЙ ФУНКЦИИ
Презентация на тему ПРОИЗВОДНАЯ СТЕПЕННОЙ ФУНКЦИИ  Таблицы, часть 1, 5-9 классы
Таблицы, часть 1, 5-9 классы Predel_funktsii_v_tochke
Predel_funktsii_v_tochke Цилиндр, конус, шар. Решение задач
Цилиндр, конус, шар. Решение задач Название круглых сотен
Название круглых сотен Треугольник и его виды
Треугольник и его виды Классическое определение вероятности
Классическое определение вероятности Множества и операции над ними
Множества и операции над ними Reshenie_zadach_1
Reshenie_zadach_1 Площадь параллелограмма
Площадь параллелограмма Десятичные дроби. Тест
Десятичные дроби. Тест Система географических координат
Система географических координат Интерактивная игра-тренажёр. Считаем с Лунтиком (2 класс). Умножение и деление на 5
Интерактивная игра-тренажёр. Считаем с Лунтиком (2 класс). Умножение и деление на 5 Диаграммы. Фронтальная работа. 6 класс
Диаграммы. Фронтальная работа. 6 класс неопред интеграл
неопред интеграл Презентация на тему Математический КВН
Презентация на тему Математический КВН  Математическое моделирование. Основные положения
Математическое моделирование. Основные положения Математический диктант №2. Геометрия 7класс. Первый признак равенства треугольников
Математический диктант №2. Геометрия 7класс. Первый признак равенства треугольников