Многогранник

Тетраэдр
Каждая грань многогранника – правильный треугольник.
Это многогранник называется правильный тетраэдр.

Гексаэдр
Каждая грань многогранника – квадрат.
Этот многогранник называется правильный гексаэдр или куб.

Октаэдр
Каждая грань многогранника – правильный треугольник.
Этот многогранник называется правильный октаэдр.

Додекаэдр
Каждая грань многогранника – правильный пятиугольник.
Этот многогранник называется правильный додекаэдр.

Икосаэдр
Каждая грань многогранника – правильный треугольник.
Этот многогранник называется правильный икосаэдр.

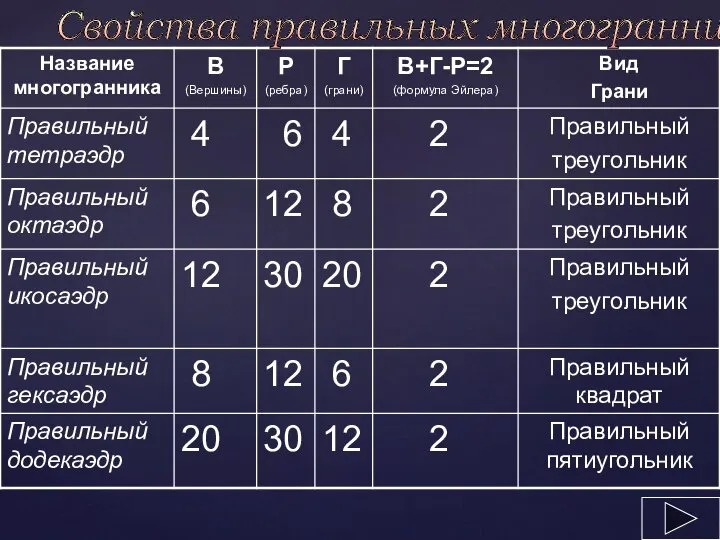
Свойства правильных многогранников

Леонард Эйлер
(1707 – 1783 гг.)
немецкий математик и физик
Формула Эйлера
(для правильных многогранников):
Г + В – Р = 2

Иоганн Кеплер
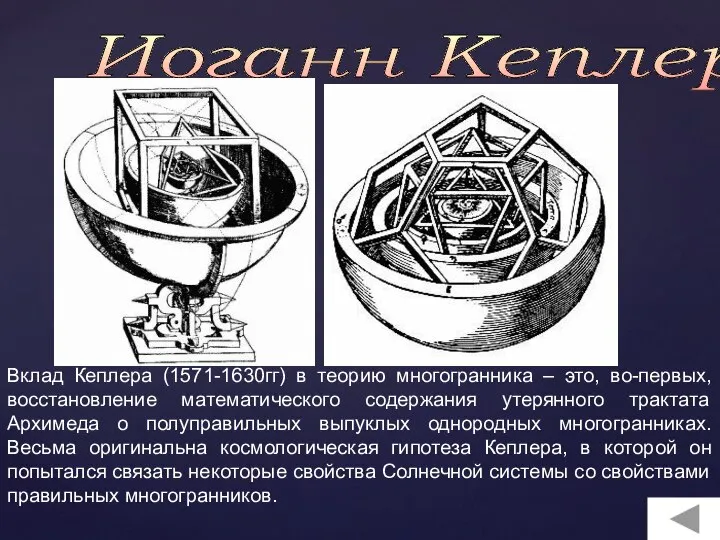
Вклад Кеплера (1571-1630гг) в теорию многогранника – это, во-первых, восстановление математического содержания утерянного трактата Архимеда о полуправильных выпуклых однородных многогранниках. Весьма оригинальна космологическая гипотеза Кеплера, в которой он попытался связать некоторые свойства Солнечной системы со свойствами правильных многогранников.

Тела Кеплера-Пуансо

Букет Пуансо
Букет Платона

Многогранники в искусстве
Альбрехт Дюрер «меланхолия»

Звёздчатый октаэдр
У октаэдра есть только одна звездчатая форма. Её можно рассматривать как соединение двух тетраэдров.

Большой звёздчатый додекаэдр
Большой звездчатый додекаэдр принадлежит к семейству тел Кеплера-Пуансо, то есть правильных невыпуклых многогранников. Грани большого звездчатого додекаэдра – пентаграммы, как и у малого звездчатого додекаэдра. У каждой вершины соединяются три грани. Вершины большого звездчатого додекаэдра совпадают с вершинами описанного додекаэдра.
Большой звездчатый додекаэдр был впервые описан Кеплером в 1619 г. Это последняя звездчатая форма правильного додекаэдра.

Икосаэдр
Икосаэдр имеет 20 граней. Если каждую из них продолжить неограниченно, то тело будет окружено великим многообразием отсеков-частей пространства, ограниченных плоскостями граней. Все звёздчатые формы икосаэдра можно получить добавлением к исходному телу таких отсеков. Не считая самого икосаэдра, продолжения его граней отделяют от пространства 20+30+60+120+20+60+12+30+60+60 отсеков десяти различных форм и размеров. Большой икосаэдр состоит из всех этих кусков, за исключением последних шестидесяти.

Икосододекаэдр
Икосододекаэдр имеет 32 грани, из которых 12 являются правильными пятиугольными гранями, а остальные 20 – правильные треугольники. Что касается вопроса о том, могут ли получившиеся многогранники оказаться правильными, то на него давно получен ответ. Великий математик Каши ещё в 1811 году доказал, что список правильных многогранников исчерпывается пятью Платоновыми телами вкупе с четырьмя многогранниками Кеплера - Пуансо.

Тайная Вечеря

Примеры

Многогранники в архитектуре
Музей Плодов в Яманаши Ицуко Хасегава

Великая пирамида в Гизе

Великие пирамиды в Гизе

Александрийский маяк

Фаросский маяк