Слайд 2Понятие вектора
А
В
Отрезок, для которого указано, какой из
его концов считается началом,
а какой
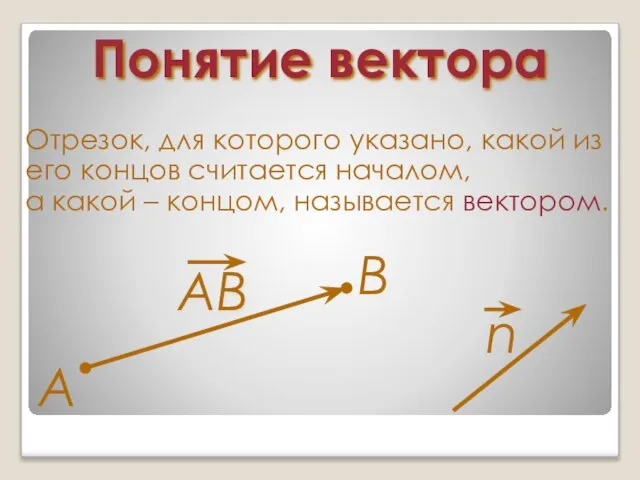
– концом, называется вектором.
Слайд 3Нулевой вектор
Любая точка на плоскости может рассматриваться как вектор.
М
Такой вектор называется

нулевым.
Слайд 5Коллинеарность векторов
Два ненулевых вектора называются
коллинеарными, если они лежат на одной
прямой

или на параллельных прямых.
Слайд 6Сонаправленные векторы
Два коллинеарных вектора
называются сонаправленными,
если у них совпадают направления.

Слайд 7Противоположно направленные векторы
Два коллинеарных вектора называются
противоположно направленными, если
они не сонаправлены.

Слайд 8Равные векторы
Векторы называются равными, если
они сонаправлены и их длины равны.

Слайд 9Откладывание вектора от данной точки
А
В
М
N

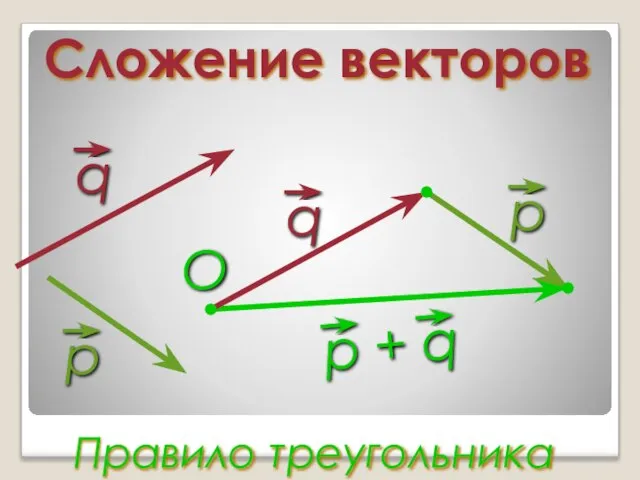
Слайд 10Сложение векторов
Правило треугольника
O
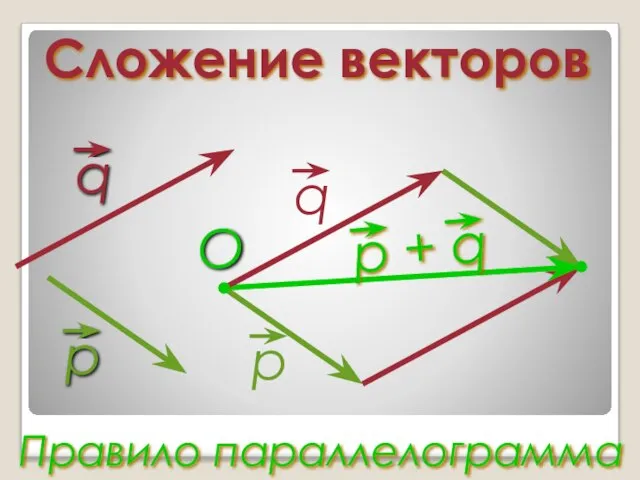
Слайд 11Сложение векторов
Правило параллелограмма
O
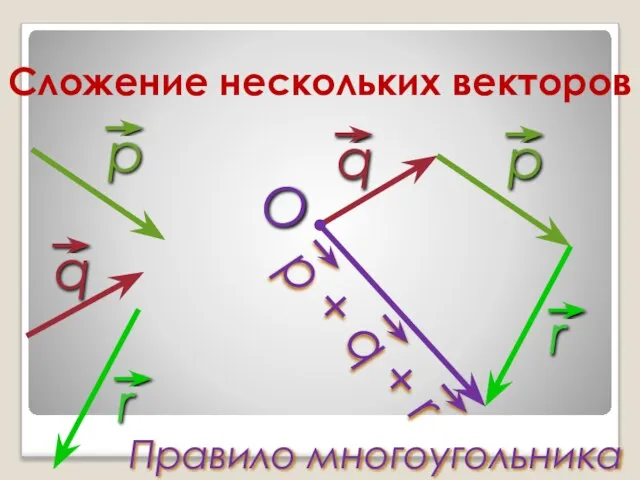
Слайд 12Сложение нескольких векторов
O
Правило многоугольника
Слайд 13Свойства сложения
− переместительный закон
− сочетательный закон
− разность векторов

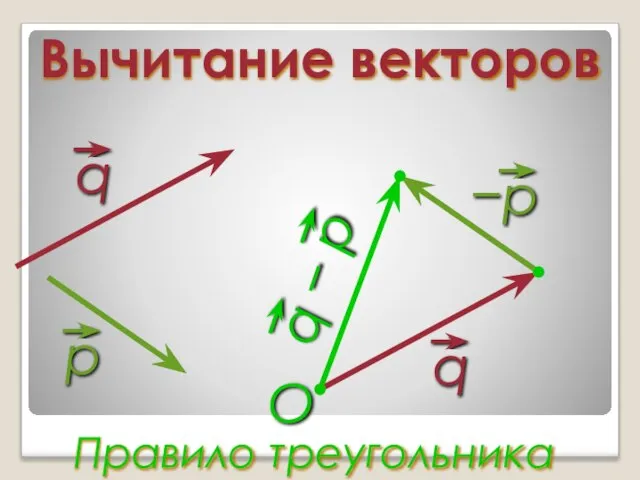
Слайд 14Вычитание векторов
Правило треугольника
O
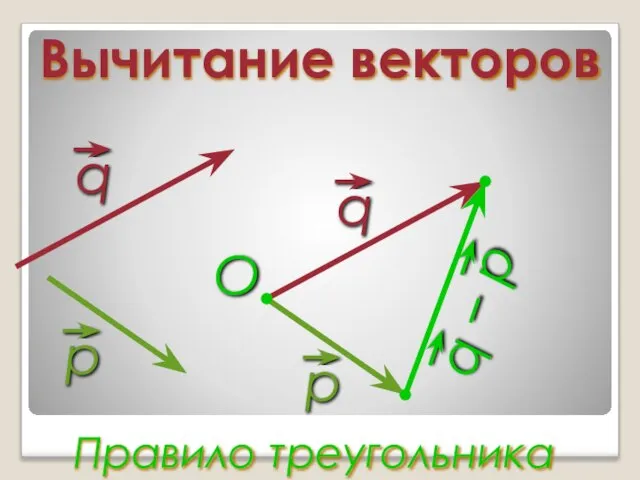
Слайд 15Вычитание векторов
Правило треугольника
O
Слайд 16Умножение вектора
на число
Коллинеарны
















 Момент силы относительно точки О
Момент силы относительно точки О Координатный метод в решении задач на плоскости Белобородова Н. Е., учитель математики МАОУ «СОШ №2»
Координатный метод в решении задач на плоскости Белобородова Н. Е., учитель математики МАОУ «СОШ №2»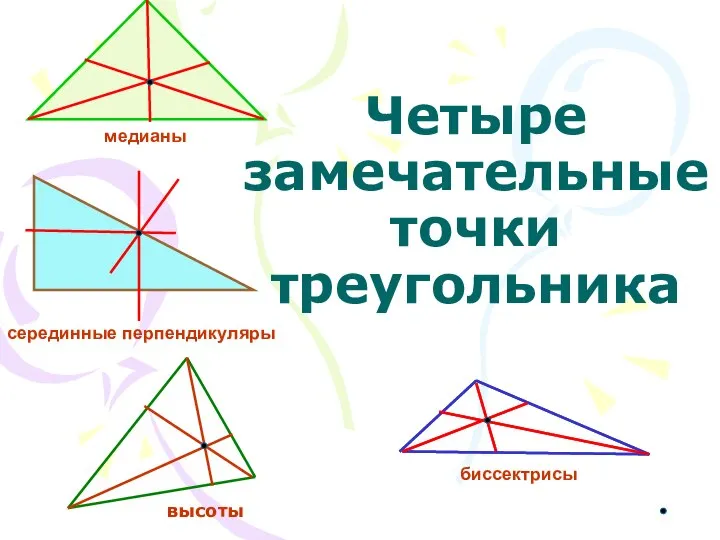 Четыре замечательные точки треугольника
Четыре замечательные точки треугольника Производная суммы, произведения и частного двух функций
Производная суммы, произведения и частного двух функций Задачи на построение сечений. 10 класс
Задачи на построение сечений. 10 класс Площадь ромба
Площадь ромба Проценты. Задачи на концентрацию, сплавы. ЕГЭ В11
Проценты. Задачи на концентрацию, сплавы. ЕГЭ В11 Расширение и углубление знаний учащихся о преобразованиях графиков функций
Расширение и углубление знаний учащихся о преобразованиях графиков функций 2._3
2._3 Խնդիր Հաշվել a, b, c կողմեր ունեցող եռանկյան մակերեսը
Խնդիր Հաշվել a, b, c կողմեր ունեցող եռանկյան մակերեսը Основные тригонометрические тождества. Формулы приведения
Основные тригонометрические тождества. Формулы приведения Решение уравнений. Буквенные выражения
Решение уравнений. Буквенные выражения Выделение целой части из неправильной дроби и представление смешанной дроби в виде неправильной
Выделение целой части из неправильной дроби и представление смешанной дроби в виде неправильной Взаимное расположение прямой и окружности (7 класс)
Взаимное расположение прямой и окружности (7 класс) Геометрия и искусство
Геометрия и искусство Формулы двойного аргумента
Формулы двойного аргумента Вариационно-статистический метод анализа
Вариационно-статистический метод анализа Занимательная математика.Игры с кубиками, 1 класс
Занимательная математика.Игры с кубиками, 1 класс Таблица умножения на 2
Таблица умножения на 2 Цифра 10
Цифра 10 Координатная плоскость
Координатная плоскость Презентация на тему Евклид
Презентация на тему Евклид  Задания для домашнего обучения
Задания для домашнего обучения Понятие теории игр
Понятие теории игр Иррациональные уравнения (часть 1)
Иррациональные уравнения (часть 1) Углы треугольника
Углы треугольника Математическое моделирование. Линейное программирование
Математическое моделирование. Линейное программирование Рівнобедрений трикутник і його властивості
Рівнобедрений трикутник і його властивості