Слайд 2Рассмотрите данные треугольники
Есть у них что-то похожее?
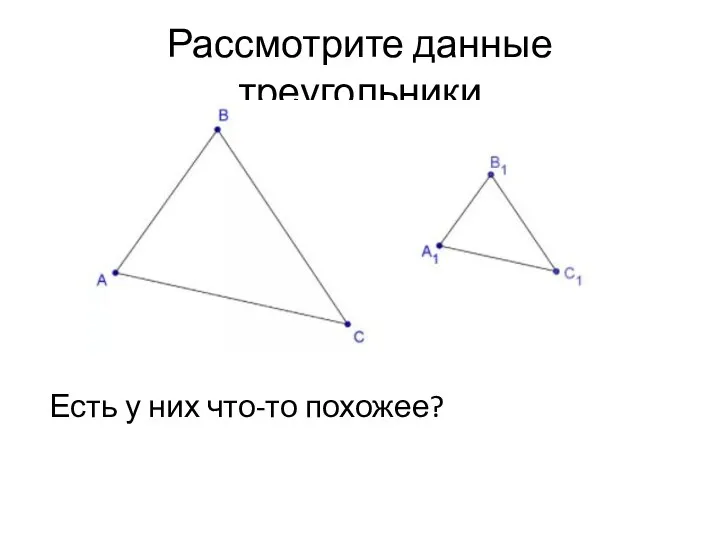
Слайд 3У треугольников равные углы, но стороны первого треугольника длиннее.
Такие треугольники называются подобными
Слайд 4Чем интересны подобные треугольники?
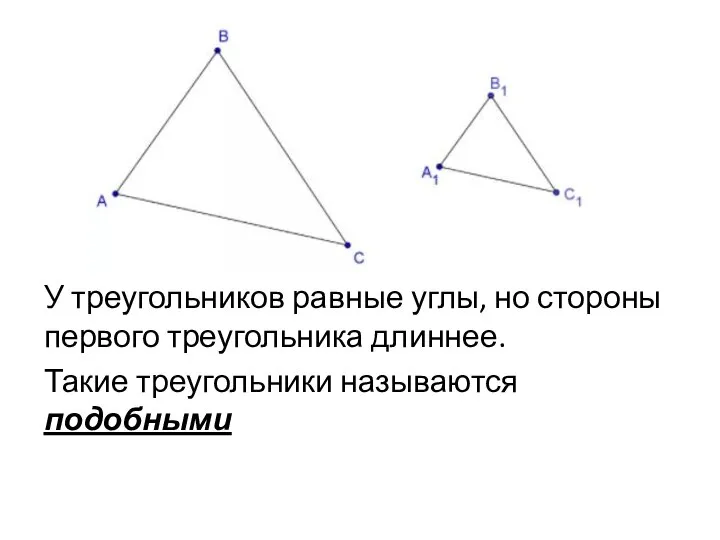
Во-первых, у них углы соответственно равны.
На данном рисунке равны
углы: А=А1, В=В1, С=С1
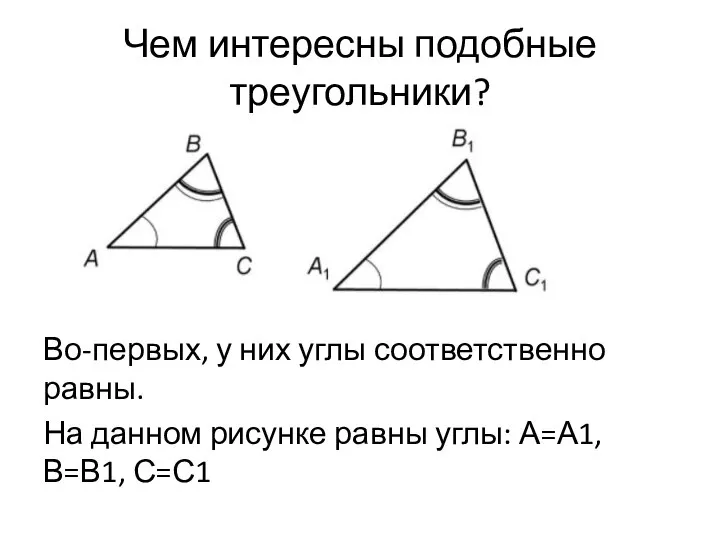
Слайд 5Что со сторонами?
Здесь немного сложней. Стороны пропорциональны. То есть, у одного треугольника
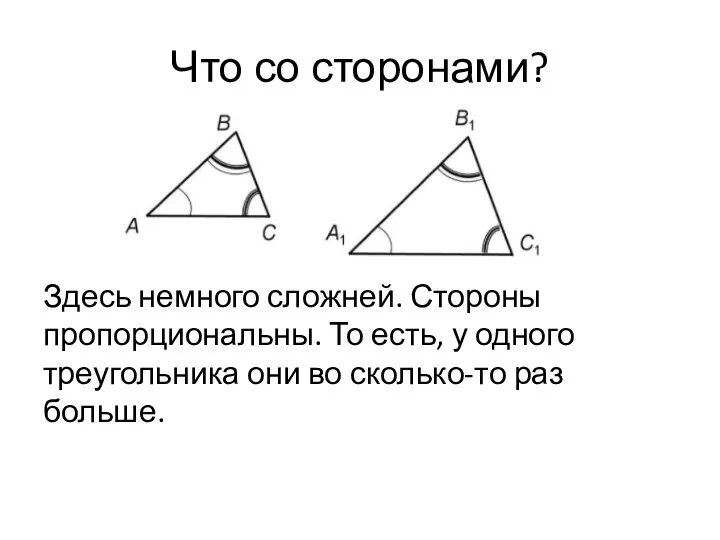
они во сколько-то раз больше.
Слайд 6Если разделить сходственные стороны, то мы получим число. Причем для всех сходственных
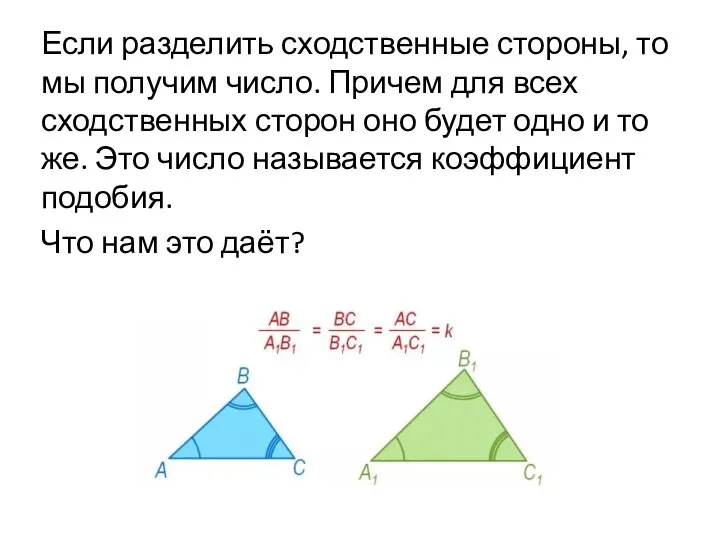
сторон оно будет одно и то же. Это число называется коэффициент подобия.
Что нам это даёт?
Слайд 7Мы можем найти стороны треугольника, пользуясь этим свойством. Пример: (на рис.)
Необходимо найти
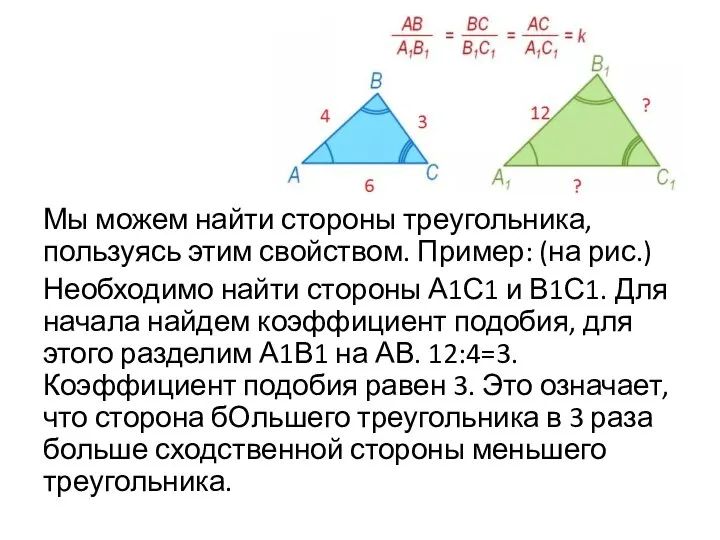
стороны А1С1 и В1С1. Для начала найдем коэффициент подобия, для этого разделим А1В1 на АВ. 12:4=3. Коэффициент подобия равен 3. Это означает, что сторона бОльшего треугольника в 3 раза больше сходственной стороны меньшего треугольника.






 Подготовка к контрольной работе
Подготовка к контрольной работе Расстояние между точками с заданными координатами. Координаты середины отрезка
Расстояние между точками с заданными координатами. Координаты середины отрезка Урок по алгебре и началам анализа. Форма проведения - деловая игра Выборы!
Урок по алгебре и началам анализа. Форма проведения - деловая игра Выборы! Окружность. 7 класс
Окружность. 7 класс Пирамиды. Объём пирамиды
Пирамиды. Объём пирамиды Теория вероятности. Сокращение дробей
Теория вероятности. Сокращение дробей Приёмы устных вычислений вида 240 ● 4, 203 ● 4, 960 : 3
Приёмы устных вычислений вида 240 ● 4, 203 ● 4, 960 : 3 Какие бывают числа
Какие бывают числа Дроби и проценты. Построение диаграмм
Дроби и проценты. Построение диаграмм Среднее арифметическое
Среднее арифметическое О треугольниках
О треугольниках Квадрат та його властивості
Квадрат та його властивості #УчимсяСМарусей. Фрагмент урока математики в 5 классе с использованием умной колонки
#УчимсяСМарусей. Фрагмент урока математики в 5 классе с использованием умной колонки Роль диагностики в обучении математи
Роль диагностики в обучении математи Основные постулаты
Основные постулаты krivye-vtorogo-poryadka
krivye-vtorogo-poryadka формулы
формулы Основные тригонометрические тождества. Преобразование тригонометрических выражений
Основные тригонометрические тождества. Преобразование тригонометрических выражений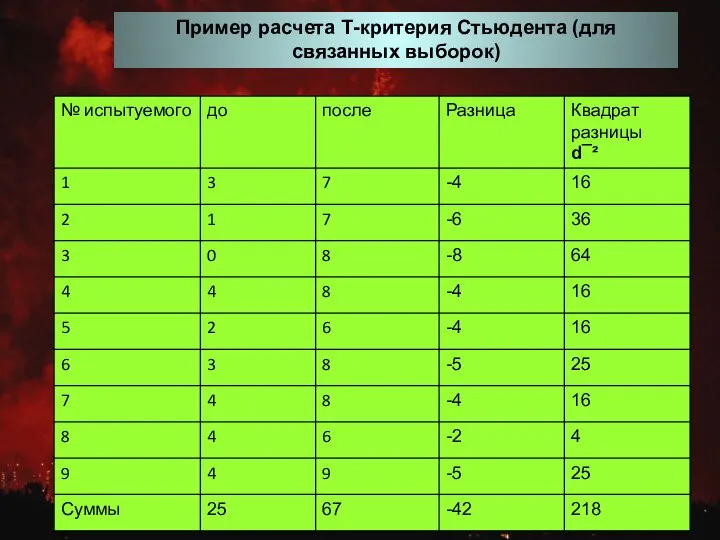 Пример расчета Т-критерия Стьюдента (для связанных выборок)
Пример расчета Т-критерия Стьюдента (для связанных выборок) Теоремы Чевы и Менелая
Теоремы Чевы и Менелая Графическое решение задач
Графическое решение задач Решение задач
Решение задач Урок математики в 1 классе
Урок математики в 1 классе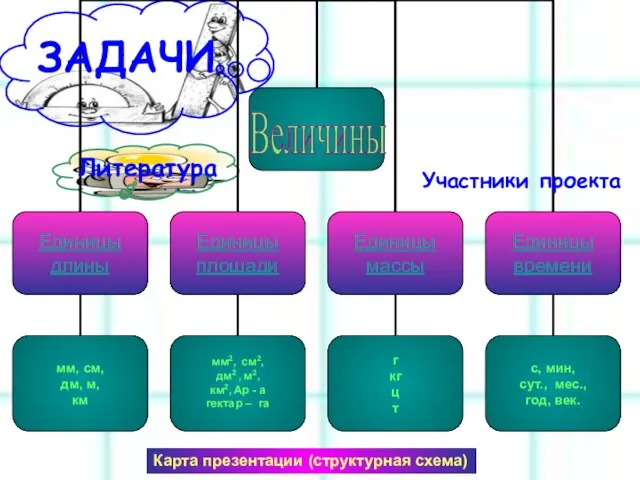 Презентация на тему Величины (4 класс)
Презентация на тему Величины (4 класс)  Законы алгебры логики. Задания
Законы алгебры логики. Задания Число и цифра 3
Число и цифра 3 Построение биссектрисы угла. Билеты
Построение биссектрисы угла. Билеты Область определения и множество значений тригонометрических функций
Область определения и множество значений тригонометрических функций