Функция y=cosx и окружающий нас мир

Функция y = cos x определена на всей числовой прямой, и множеством её значений является отрезок [−1;1].
Следовательно, график этой функции расположен в полосе между прямыми y= −1 и y=1.
Так как функция y = cos x периодическая с периодом 2π, то достаточно построить её график на каком-нибудь промежутке длиной 2π, тогда на промежутках, получаемых сдвигами выбранного отрезка на 2πn, n∈Z, график будет таким же.

Рассмотрим поведение функции и отметим важнейшие точки на промежутке [0;π]
В координатной плоскости
На числовой окружности

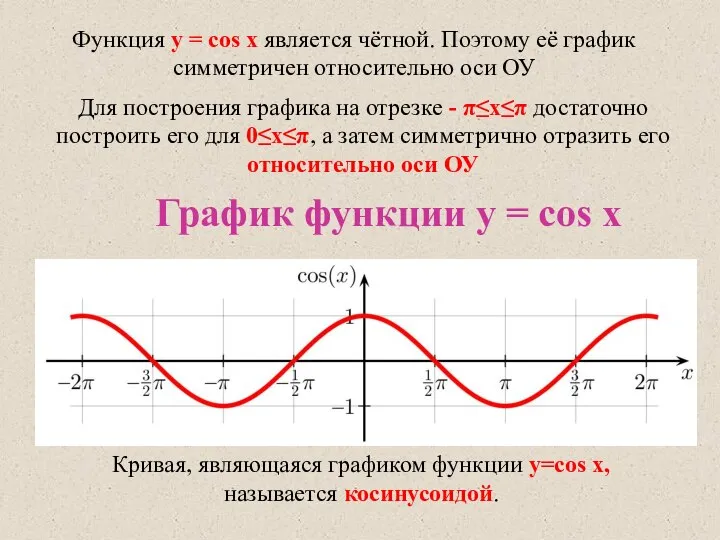
Функция y = cos x является чётной. Поэтому её график симметричен относительно оси ОУ
Для построения графика на отрезке - π≤x≤π достаточно построить его для 0≤x≤π, а затем симметрично отразить его относительно оси ОУ
График функции y = cos x
Кривая, являющаяся графиком функции y=cos x, называется косинусоидой.

Свойства функции y = cos x
1. Область определения — множество R всех действительных чисел. D(y) = (-∞; + ∞)
2. Множество значений Е(у) = [−1;1]
3. Функция периодическая с периодом T= 2π.
4. Функция чётная cos(-x) = cos x
(график симметричен относительно оси ОУ).
5. Функция ограничена и сверху, и снизу.
6. Функция y=cos x принимает:
- значение, равное 0, при x=π/2+πn,n∈Z;
- наибольшее значение, равное 1, при x=2πn,n∈Z;
- наименьшее значение, равное −1, при x=π+2πn,n∈Z;

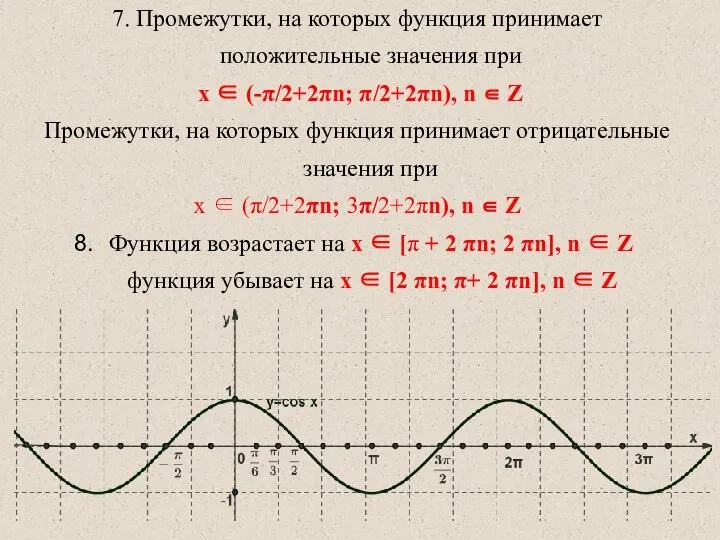
7. Промежутки, на которых функция принимает положительные значения при
x ∈ (-π/2+2πn; π/2+2πn), n ∈ Z
Промежутки, на которых функция принимает отрицательные значения при
x ∈ (π/2+2πn; 3π/2+2πn), n ∈ Z
Функция возрастает на x ∈ [π + 2 πn; 2 πn], n ∈ Z
функция убывает на x ∈ [2 πn; π+ 2 πn], n ∈ Z

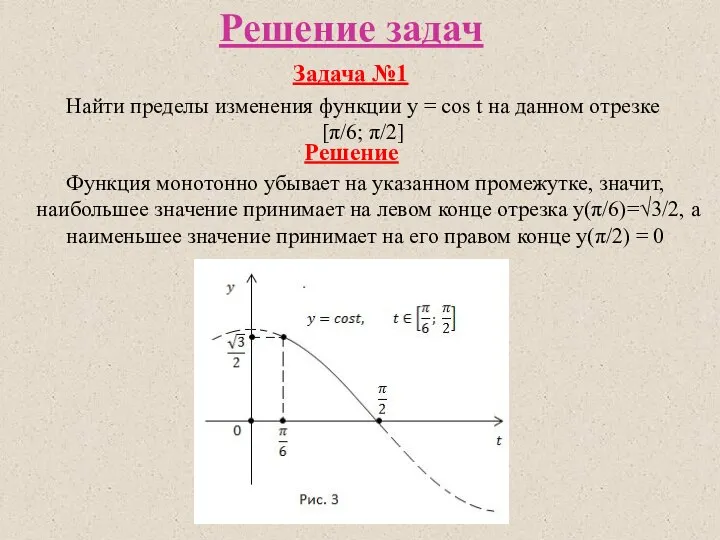
Решение задач
Задача №1
Найти пределы изменения функции y = cos t на данном отрезке [π/6; π/2]
Функция монотонно убывает на указанном промежутке, значит, наибольшее значение принимает на левом конце отрезка у(π/6)=√3/2, а наименьшее значение принимает на его правом конце у(π/2) = 0
Решение