Параллельные алгоритмы вычислительной алгебры. Распараллеливание на компьютерах с распределенной памятью
Содержание
- 2. Часть 5: Распараллеливание на компьютерах с распределенной памятью Linpack LAPACK DAG алгоритм
- 3. Blas Basic Linear Algebra Subprograms - BLAS Level 1 – операции с векторами (скалярное произведение вектор,
- 4. Linpack Linear Algebra Package Пакет для решения систем линейных уравнений и задачи о наименьших квадратах Опубликован
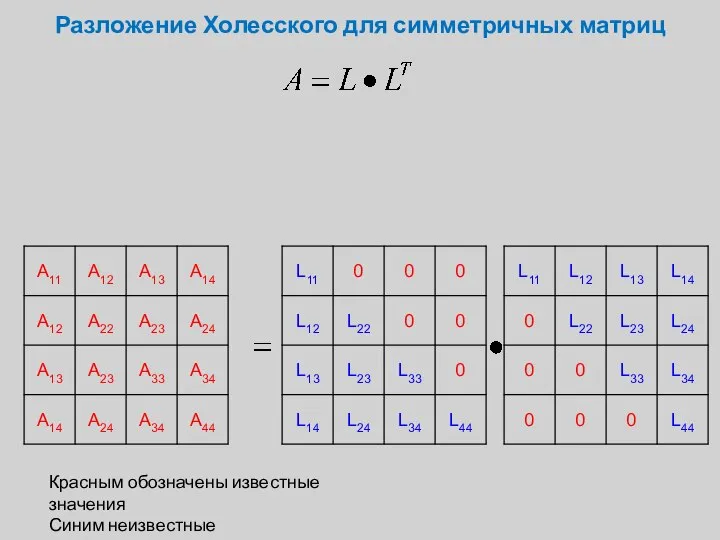
- 5. Разложение Холесского для симметричных матриц Красным обозначены известные значения Синим неизвестные
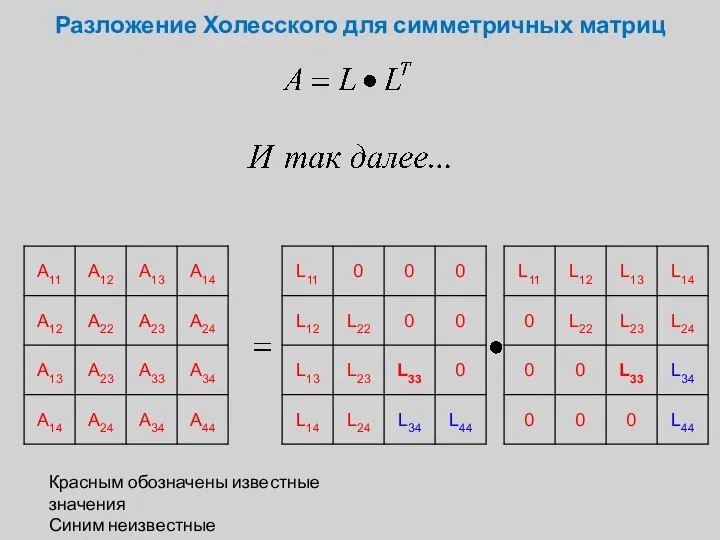
- 6. Разложение Холесского для симметричных матриц Красным обозначены известные значения Синим неизвестные
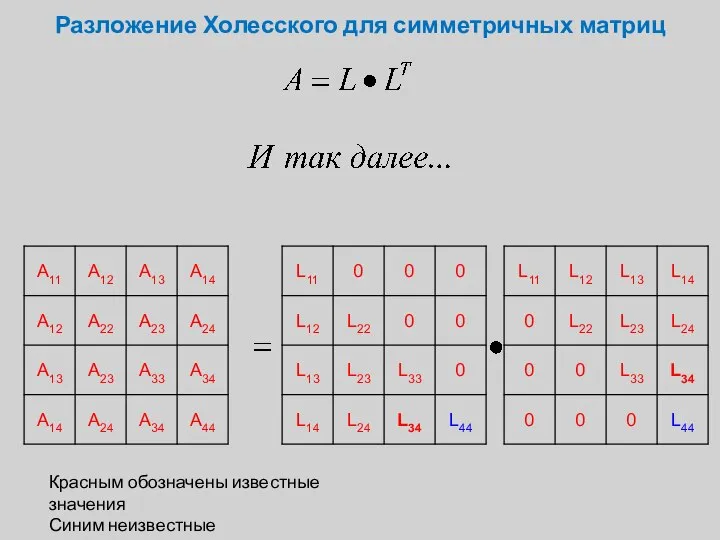
- 7. Разложение Холесского для симметричных матриц Красным обозначены известные значения Синим неизвестные
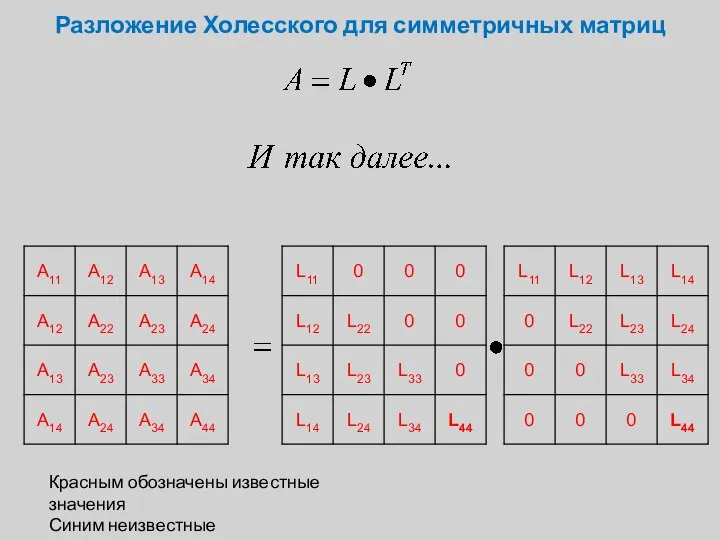
- 8. Разложение Холесского для симметричных матриц Красным обозначены известные значения Синим неизвестные
- 9. Разложение Холесского для симметричных матриц Красным обозначены известные значения Синим неизвестные
- 10. Разложение Холесского для симметричных матриц Красным обозначены известные значения Синим неизвестные
- 11. Разложение Холесского для симметричных матриц Красным обозначены известные значения Синим неизвестные
- 12. Разложение Холесского для симметричных матриц Красным обозначены известные значения Синим неизвестные
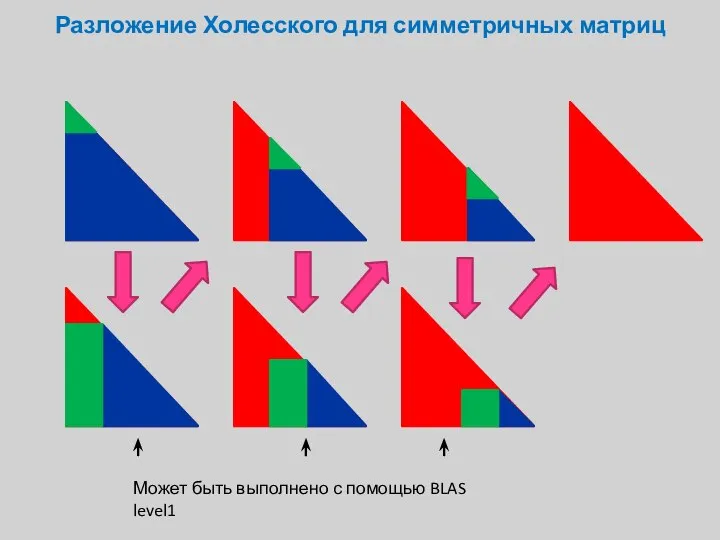
- 13. Разложение Холесского для симметричных матриц Может быть выполнено с помощью BLAS level1
- 14. Linpack Плюсы: Достаточно оптимизировать BLAS level 1 для процессора, чтоб получить оптимизированный Linpack Минусы: При увеличении
- 15. LAPACK Linear Algebra Package Пакет для решения систем линейных уравнений, поиска сингулярных значений матриц, задач о
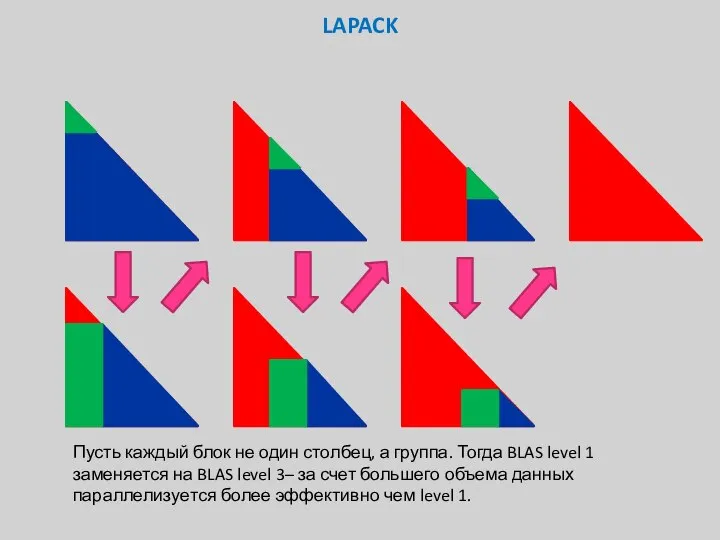
- 16. LAPACK Пусть каждый блок не один столбец, а группа. Тогда BLAS level 1 заменяется на BLAS
- 17. LAPACK Плюсы: Достаточно оптимизировать BLAS level 3 для процессора, чтоб получить оптимизированное разложение Холесского Минусы: Не
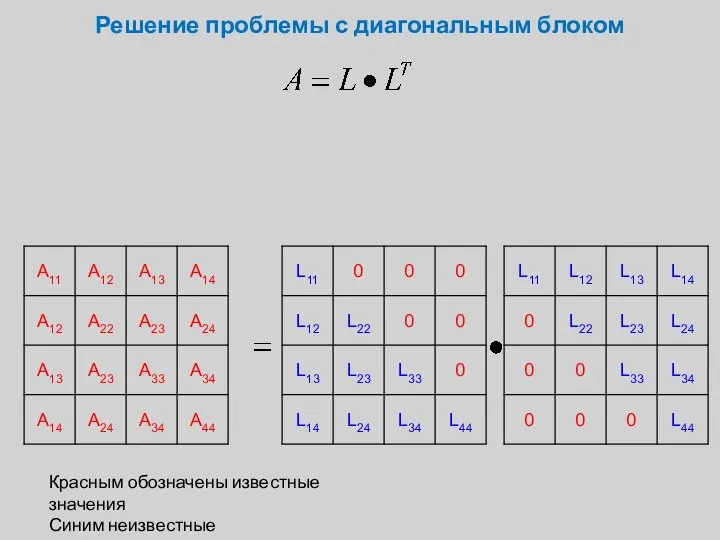
- 18. Решение проблемы с диагональным блоком Красным обозначены известные значения Синим неизвестные
- 19. Решение проблемы с диагональным блоком Красным обозначены известные значения Синим неизвестные
- 20. Решение проблемы с диагональным блоком Красным обозначены известные значения Синим неизвестные
- 21. Решение проблемы с диагональным блоком Красным обозначены известные значения Синим неизвестные
- 22. Разложение Холесского для симметричных матриц Красным обозначены известные значения Синим неизвестные
- 23. Решение проблемы с диагональным блоком Красным обозначены известные значения Синим неизвестные
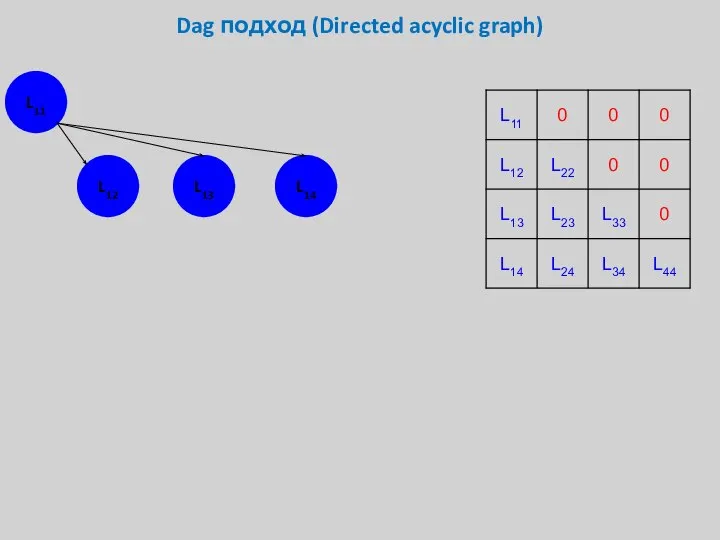
- 24. Dag подход (Directed acyclic graph) L11
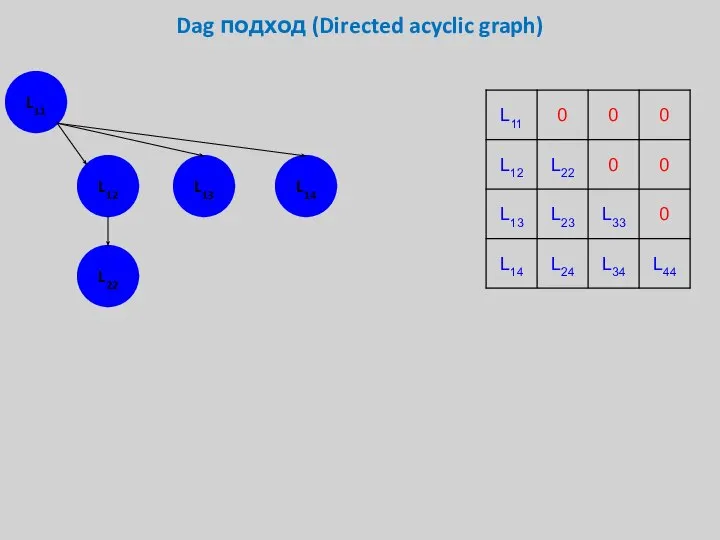
- 25. Dag подход (Directed acyclic graph) L11 L12 L13 L14
- 26. Dag подход (Directed acyclic graph) L11 L12 L13 L14 L22
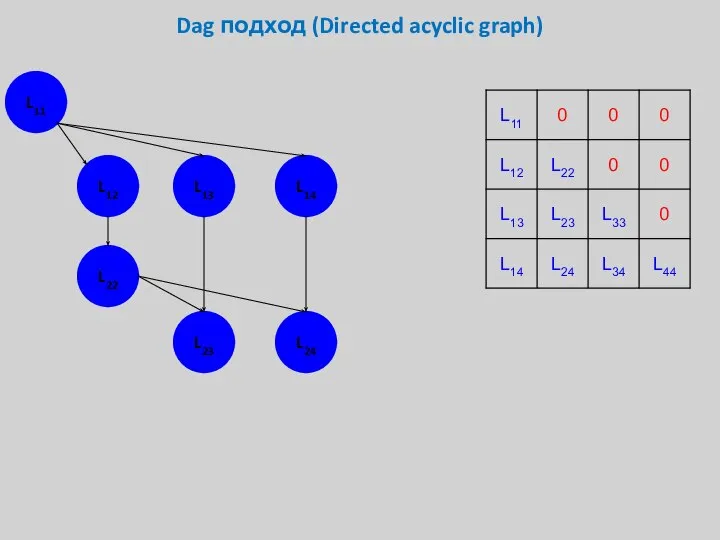
- 27. Dag подход (Directed acyclic graph) L11 L12 L13 L14 L22 L23 L24
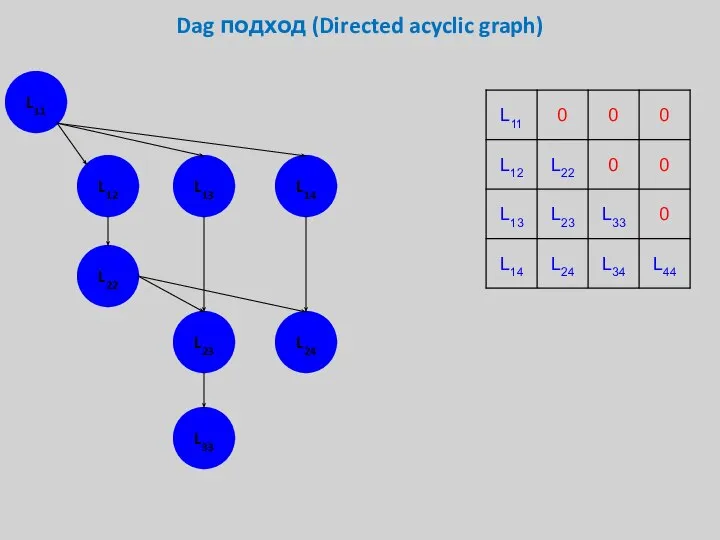
- 28. Dag подход (Directed acyclic graph) L11 L12 L13 L14 L22 L23 L24 L33
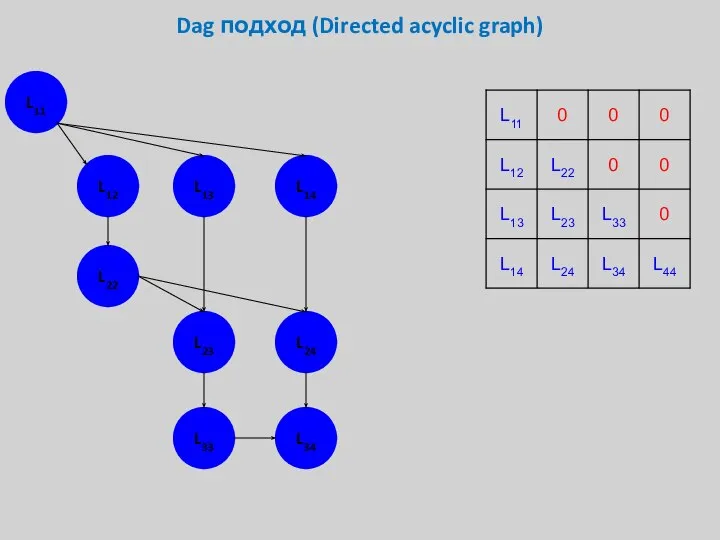
- 29. Dag подход (Directed acyclic graph) L11 L12 L13 L14 L22 L23 L24 L33 L34
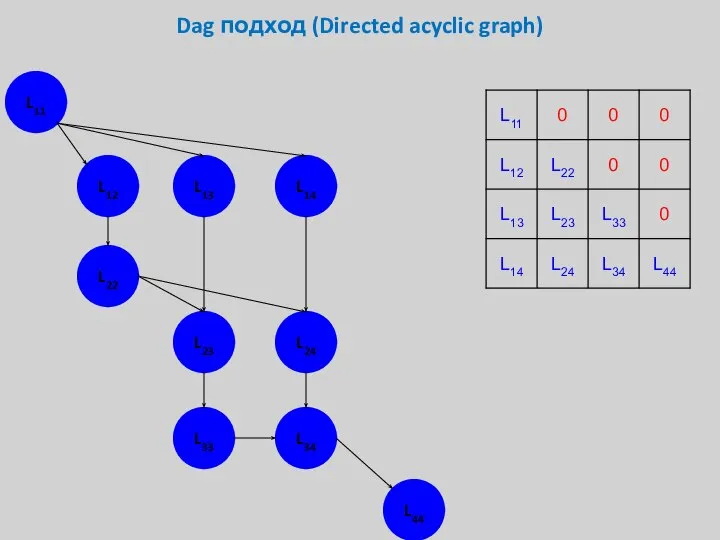
- 30. Dag подход (Directed acyclic graph) L11 L12 L13 L14 L22 L23 L24 L33 L34 L44
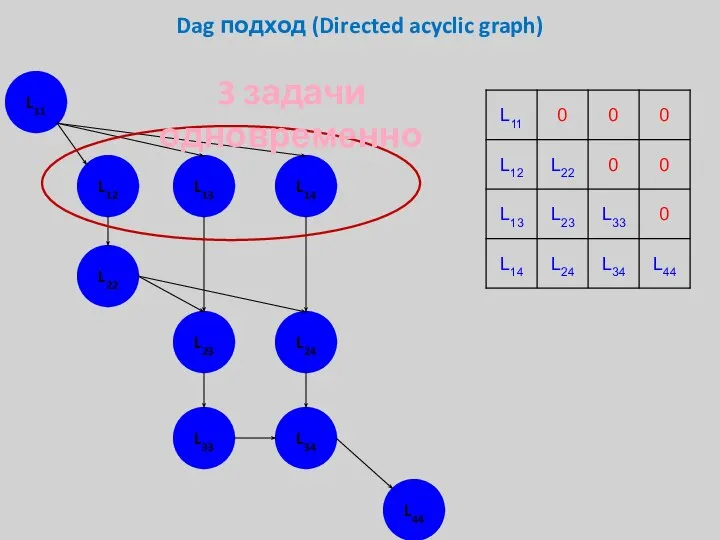
- 31. Dag подход (Directed acyclic graph) L11 L12 L13 L14 L22 L23 L24 L33 L34 L44 3
- 32. Dag подход (Directed acyclic graph) Более того, мы можем постепенно модифицировать Lij, а не только перед
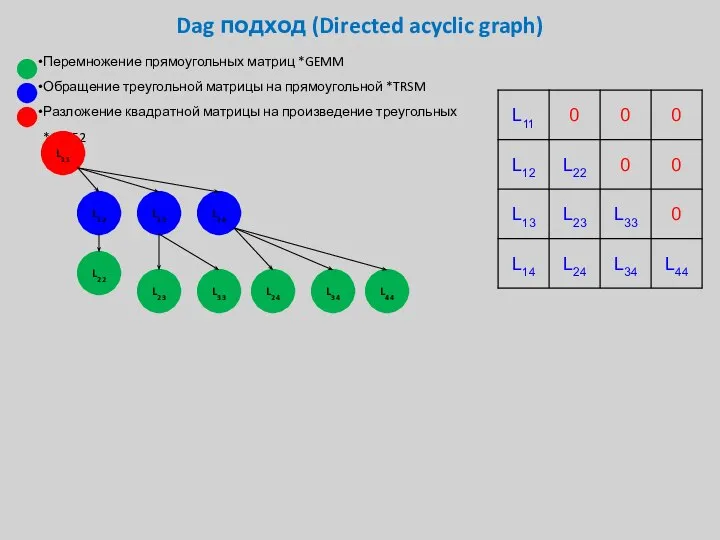
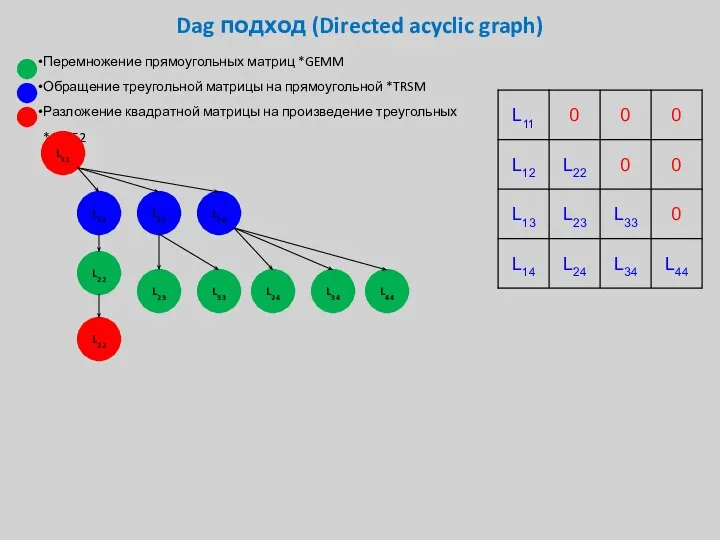
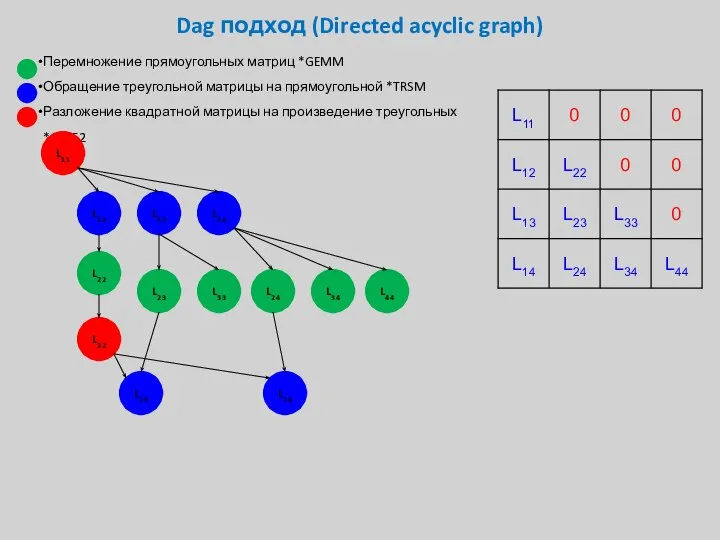
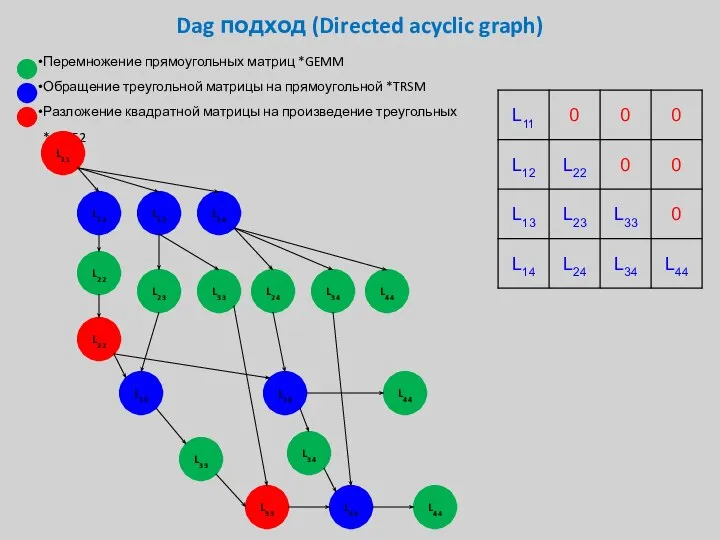
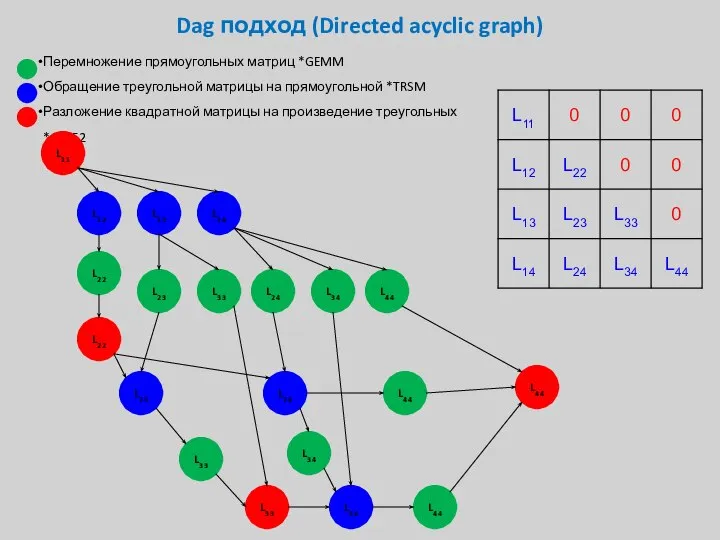
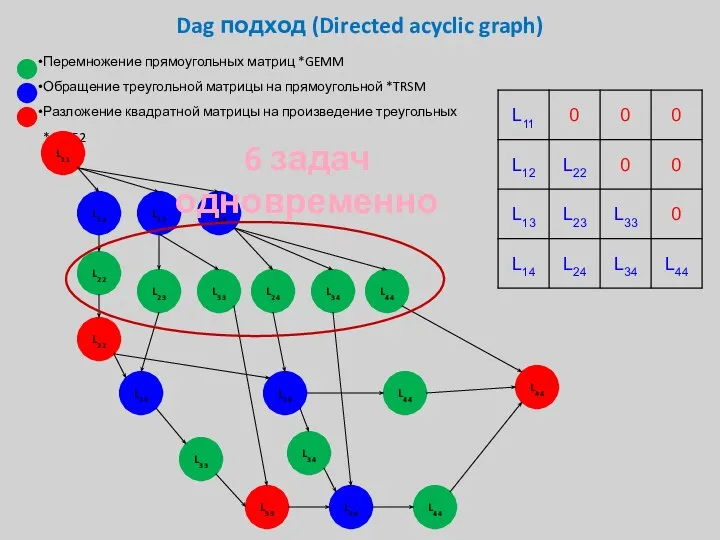
- 33. Dag подход (Directed acyclic graph) Перемножение прямоугольных матриц *GEMM Обращение треугольной матрицы на прямоугольной *TRSM Разложение
- 34. Dag подход (Directed acyclic graph) Перемножение прямоугольных матриц *GEMM Обращение треугольной матрицы на прямоугольной *TRSM Разложение
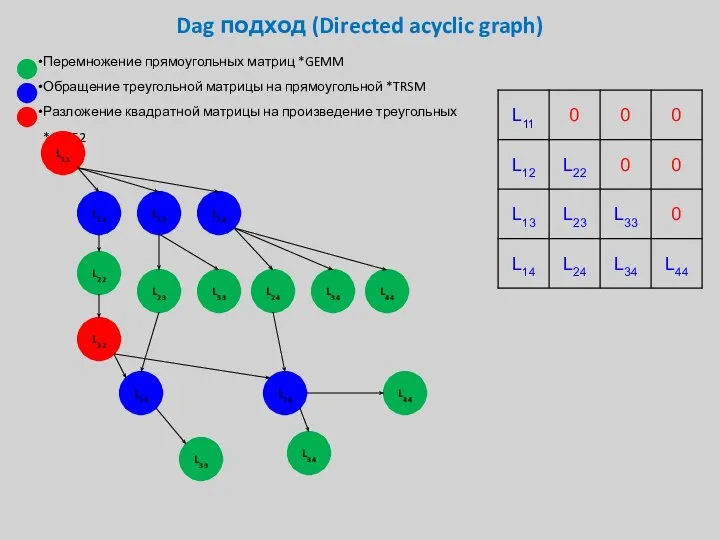
- 35. Dag подход (Directed acyclic graph) Перемножение прямоугольных матриц *GEMM Обращение треугольной матрицы на прямоугольной *TRSM Разложение
- 36. Dag подход (Directed acyclic graph) Перемножение прямоугольных матриц *GEMM Обращение треугольной матрицы на прямоугольной *TRSM Разложение
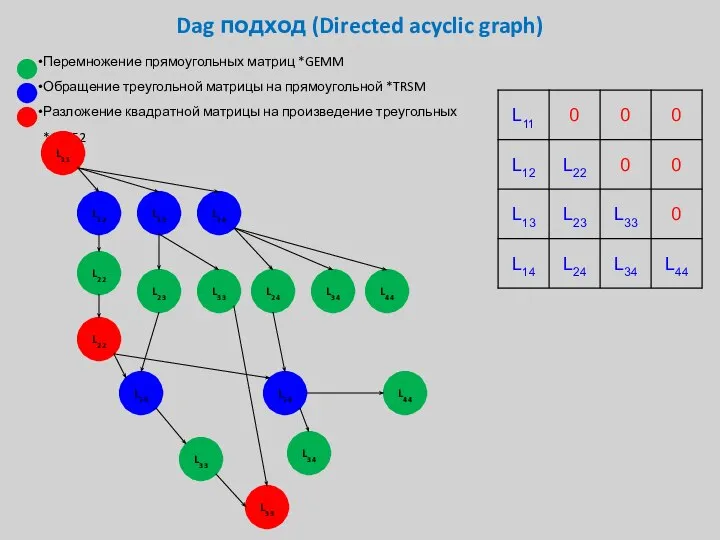
- 37. Dag подход (Directed acyclic graph) Перемножение прямоугольных матриц *GEMM Обращение треугольной матрицы на прямоугольной *TRSM Разложение
- 38. Dag подход (Directed acyclic graph) Перемножение прямоугольных матриц *GEMM Обращение треугольной матрицы на прямоугольной *TRSM Разложение
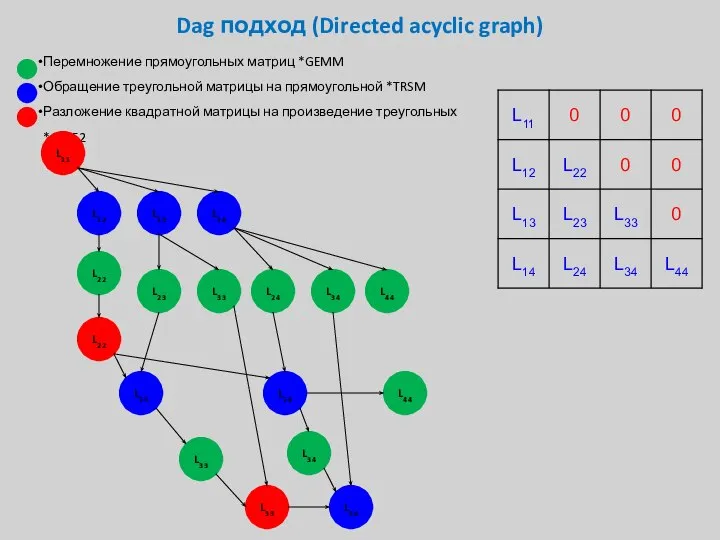
- 39. Dag подход (Directed acyclic graph) Перемножение прямоугольных матриц *GEMM Обращение треугольной матрицы на прямоугольной *TRSM Разложение
- 40. Dag подход (Directed acyclic graph) Перемножение прямоугольных матриц *GEMM Обращение треугольной матрицы на прямоугольной *TRSM Разложение
- 41. Dag подход (Directed acyclic graph) Перемножение прямоугольных матриц *GEMM Обращение треугольной матрицы на прямоугольной *TRSM Разложение
- 42. Dag подход (Directed acyclic graph) Перемножение прямоугольных матриц *GEMM Обращение треугольной матрицы на прямоугольной *TRSM Разложение
- 43. Dag подход (Directed acyclic graph) Перемножение прямоугольных матриц *GEMM Обращение треугольной матрицы на прямоугольной *TRSM Разложение
- 44. Dag подход (Directed acyclic graph) Плюсы: Очень хорошая шкалируемость на старте алгоритма Динамическое распределение задач Возможность
- 45. Далее... Как реализовать алгорититм для очень большого числа ядер (> 100)? Как модифицировать алгоритм в случае
- 47. Скачать презентацию





















 Найди фигуру (развиваем логику)
Найди фигуру (развиваем логику) Графики тригонометрических функций. 10 класс
Графики тригонометрических функций. 10 класс Отношения и пропорция
Отношения и пропорция Логарифмические уравнения и неравенства. Практическая работа
Логарифмические уравнения и неравенства. Практическая работа Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Практическое занятие №7 Минимизация логического автомата
Практическое занятие №7 Минимизация логического автомата Вырезаем квадрат
Вырезаем квадрат Подготовка к контрольной работе за полугодие
Подготовка к контрольной работе за полугодие Логарифмические уравнения и неравенства
Логарифмические уравнения и неравенства Многочлен и его стандартный вид
Многочлен и его стандартный вид Презентация на тему Параллельность прямых и плоскостей (10 класс)
Презентация на тему Параллельность прямых и плоскостей (10 класс)  Параллельные прямые. Задачи для подготовки к контрольной работе
Параллельные прямые. Задачи для подготовки к контрольной работе Пространственные векторы в асинхронном двигателе. Эйлер (1707-1783 гг)
Пространственные векторы в асинхронном двигателе. Эйлер (1707-1783 гг) Карточки по математике
Карточки по математике Математическое и сенсорное развитие детей раннего возраста
Математическое и сенсорное развитие детей раннего возраста Методика изучения длины
Методика изучения длины Математическая статистика
Математическая статистика Показатели вариации
Показатели вариации Случаи вычитания 11-
Случаи вычитания 11- Задачи на функции
Задачи на функции Сечение многогранников. Применение интерактивных методов обучения на уроках математики
Сечение многогранников. Применение интерактивных методов обучения на уроках математики Физико-математических КВН
Физико-математических КВН Группа предметов. Множество. Элемент множества. 3 класс
Группа предметов. Множество. Элемент множества. 3 класс Материал для внеклассной работы по математике. Бедный заяц (сказка)
Материал для внеклассной работы по математике. Бедный заяц (сказка) Презентация на тему Решение систем уравнений методом новой переменной
Презентация на тему Решение систем уравнений методом новой переменной  Золотое сечение. 9 класс
Золотое сечение. 9 класс Обратные задачи
Обратные задачи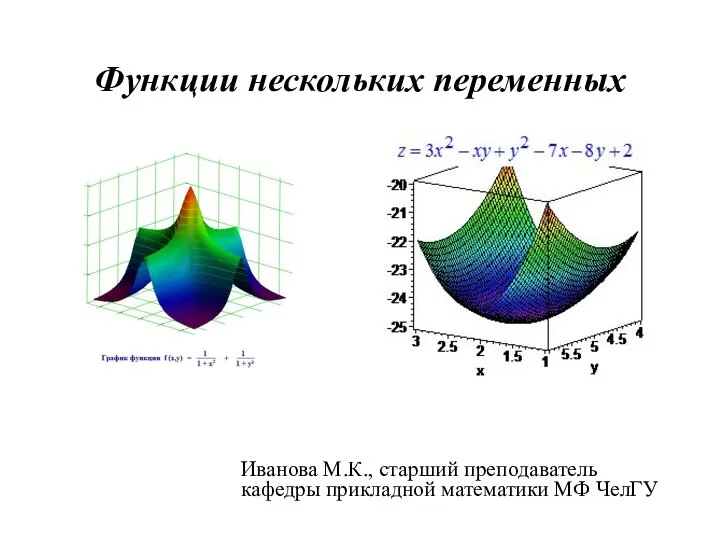 Функции нескольких переменных
Функции нескольких переменных