Содержание
- 2. Измерение центральной состоит в выборе одного числа, которое наилучшим образом описывает все значения признака из набора
- 3. Мода – наиболее часто встречающееся значение в выборке, наборе данных. Обозначается Мо. Выборка: 5,4 1,2 0,42
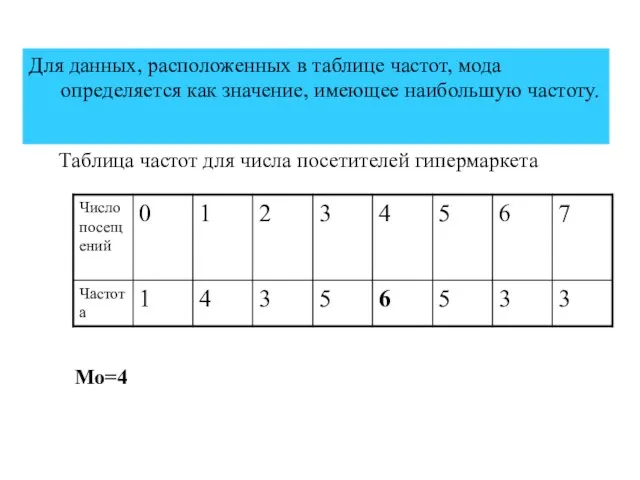
- 4. Для данных, расположенных в таблице частот, мода определяется как значение, имеющее наибольшую частоту. Таблица частот для
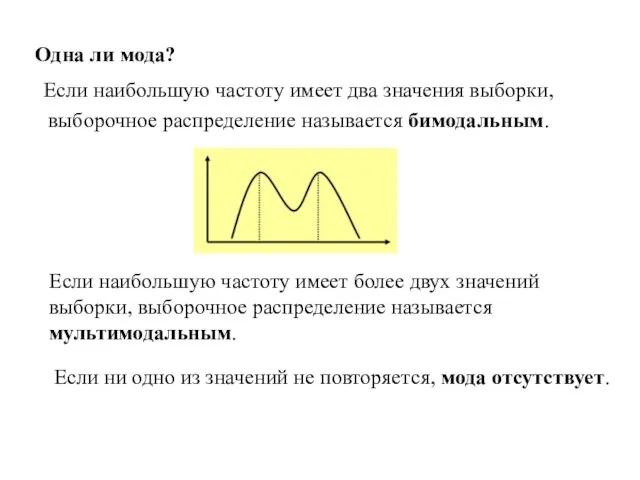
- 5. Одна ли мода? Если наибольшую частоту имеет два значения выборки, выборочное распределение называется бимодальным. Если наибольшую
- 6. Вариационный ряд Вариационный ряд - упорядоченные данные, расположенные в порядке возрастания значения признака
- 7. Медиана Если n нечетно, то медиана – это серединный элемент вариационного ряда, т.е. элемент, стоящий на
- 9. Медиана В Excel для вычисления медианы есть функция МЕДИАНА.
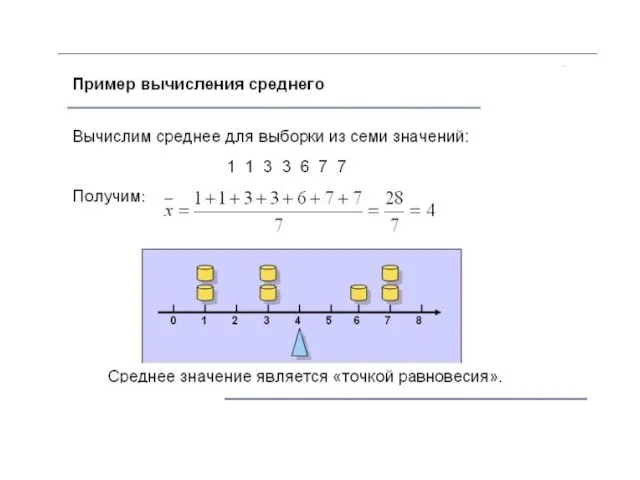
- 10. Среднее значение Выборочное среднее будем называть среднее арифметическое выборки, то есть сумму всех значений выборки, деленную
- 12. Пример. Покупателей гипермаркета попросили ответить на вопрос сколько денег в среднем они тратят при одном посещении
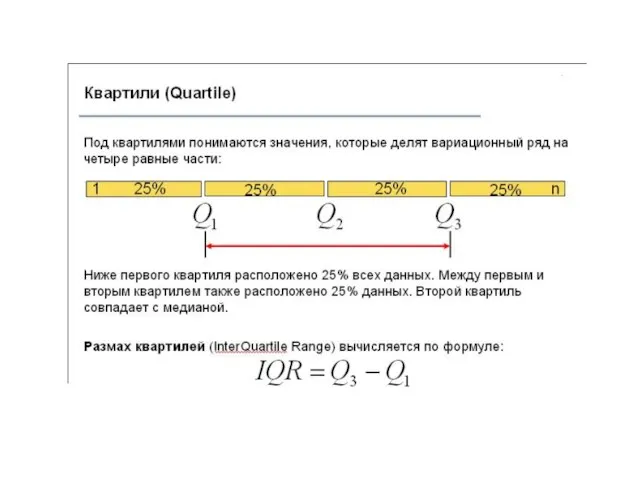
- 18. Для вычисления квартилей в Excel используется функция КВАРТИЛЬ(диапазон данных;номер квартиля) Номер квартиля – это 1,2,3
- 19. Выборочная дисперсия называется среднеквадратичным отклонением или стандартным отклонением Среднеквадратичное отклонение показывает насколько в среднем значения признака
- 21. Пример. Покупателей гипермаркета попросили ответить на вопрос сколько денег в среднем они тратят при одном посещении
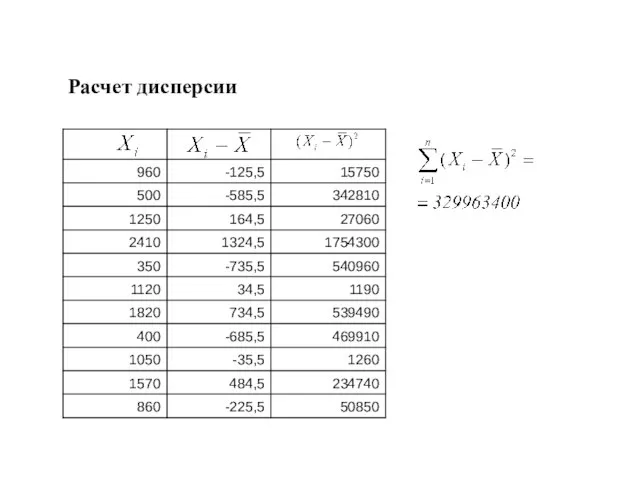
- 22. Расчет дисперсии
- 23. Расчет дисперсии
- 24. Расчет дисперсии
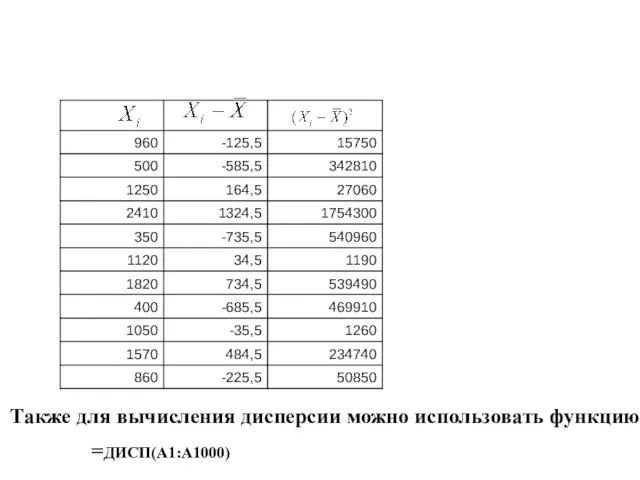
- 25. =ДИСП(A1:A1000) Также для вычисления дисперсии можно использовать функцию
- 26. Среднее отклонение потраченной суммы от среднего значения 1086 рублей равно 575 рублей.
- 27. В файле flat представлены данные о ценах на однокомнатные квартиры (тыс. USD), выставлявшихся на продажу в
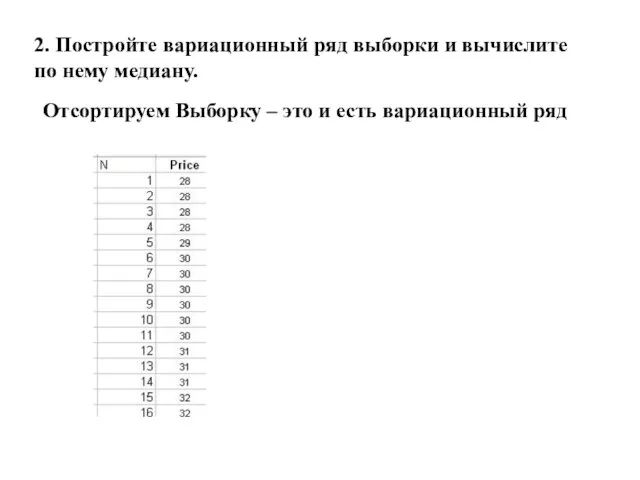
- 28. 2. Постройте вариационный ряд выборки и вычислите по нему медиану. Отсортируем Выборку – это и есть
- 29. 2. Постройте вариационный ряд выборки и вычислите по нему медиану. Отсортируем Выборку – это и есть
- 30. 2. Постройте вариационный ряд выборки и вычислите по нему медиану. Отсортируем Выборку – это и есть
- 31. 3. Вычислить медиану с помощью функции МЕДИАНА, сравните результаты.
- 32. 4. Вычислите размах выборки (см. формулу выше).
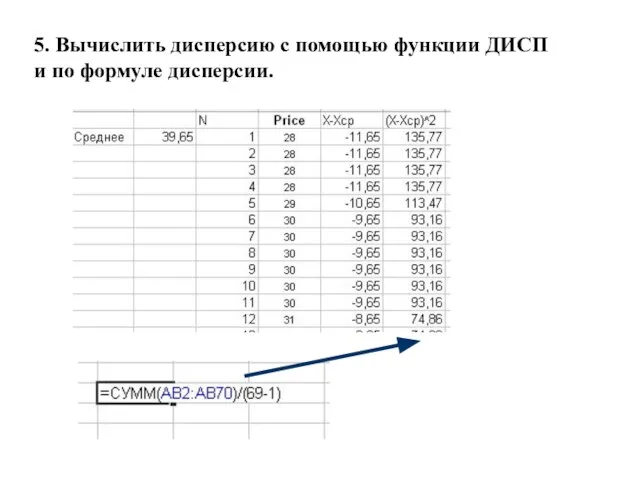
- 33. 5. Вычислить дисперсию с помощью функции ДИСП и по формуле дисперсии. См. формулу выше в слайдах
- 34. 5. Вычислить дисперсию с помощью функции ДИСП и по формуле дисперсии.
- 35. 6. Вычислить стандартное отклонение с помощью функции СТАНДОТКЛОН и по формуле стандартного отклонения.
- 36. 7. Вычислить нижний и верхний квартиль с помощью функции КВАРТИЛЬ. В качестве второго аргумента функции указать
- 38. Скачать презентацию



























 Прямоугольный параллепипед. Итоговое повторение
Прямоугольный параллепипед. Итоговое повторение Преобразование целого выражения в многочлен
Преобразование целого выражения в многочлен Тригонометрия. Учебно-игровое пособие
Тригонометрия. Учебно-игровое пособие Дискретные случайные величины
Дискретные случайные величины Геометрия в искусстве
Геометрия в искусстве Математический диктант выражениями в тетрадь
Математический диктант выражениями в тетрадь СДНФ и СКНФ — два представления булевой функции
СДНФ и СКНФ — два представления булевой функции Решение уравнений третьей степени при подготовке к ЕГЭ
Решение уравнений третьей степени при подготовке к ЕГЭ Статистическая обработка измерений
Статистическая обработка измерений Лето в цифрах. Маршрут поездки
Лето в цифрах. Маршрут поездки График функции y = kf (x)
График функции y = kf (x) Теорема о прямой, перпендикулярной к плоскости
Теорема о прямой, перпендикулярной к плоскости Равенство векторов
Равенство векторов Математика ЕГЭ. Первое занятие
Математика ЕГЭ. Первое занятие Метод Крамера
Метод Крамера Определенный интеграл. Формула Ньютона - Лейбница
Определенный интеграл. Формула Ньютона - Лейбница Деление круга на 2, 4, 8 частей
Деление круга на 2, 4, 8 частей Организация коррекционной работы по математике
Организация коррекционной работы по математике Найди соседей. Дидактическая игра
Найди соседей. Дидактическая игра Пирамида. Египетские пирамиды
Пирамида. Египетские пирамиды Числовое и буквенное выражения
Числовое и буквенное выражения Игровые моменты
Игровые моменты Переместительное свойство умножения
Переместительное свойство умножения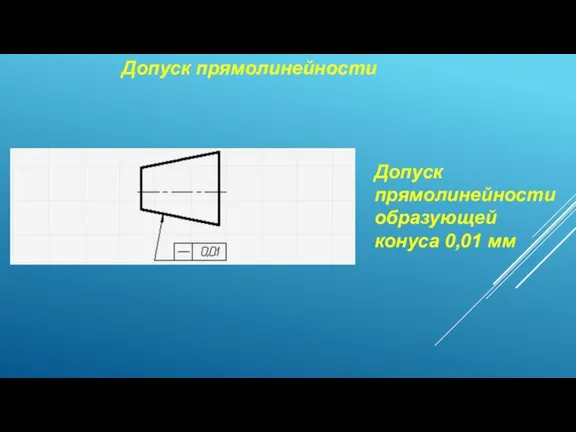 Допуск прямолинейности
Допуск прямолинейности Презентация на тему Сложение чисел с разными знаками
Презентация на тему Сложение чисел с разными знаками  Презентация на тему Перпендикулярность
Презентация на тему Перпендикулярность  Состав числа (домики)
Состав числа (домики) Элементы комбинаторики. Лекция 111
Элементы комбинаторики. Лекция 111