Содержание
- 2. При изучении реальных явлений часто бывает невозможно обследовать все элементы совокупности. Вместо изучения всех элементов совокупности,
- 3. - объем генеральной совокупности - объем репрезентативной выборки - частоты - частоты в генеральной совокупности
- 4. Для идеально составленной репрезентативной выборки должно выполняться равенство: Где i – порядковый номер значения признака (1≤i≤k).
- 5. Пример 1 Фабрика резиновых изделий выиграла тендер на изготовление армейских противогазов. Для определения того, сколько противогазов
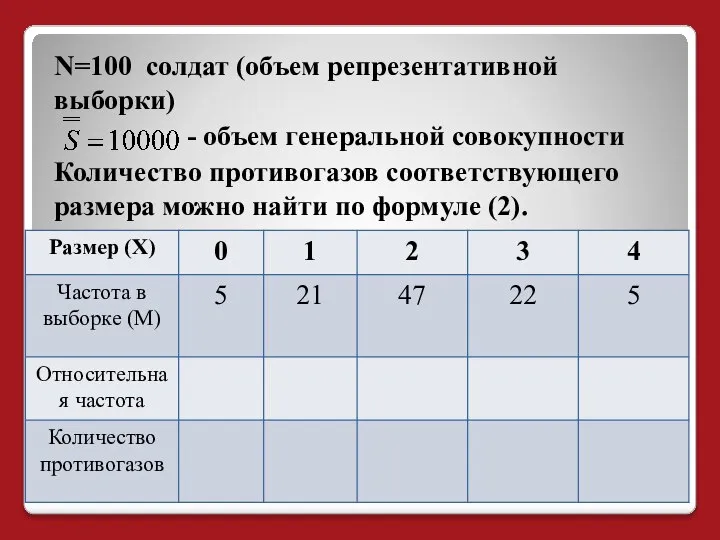
- 6. N=100 солдат (объем репрезентативной выборки) - объем генеральной совокупности Количество противогазов соответствующего размера можно найти по
- 7. Размах и центральные тенденции
- 8. 1. Размах, мода и медиана Имеются: 1) распределение случайной величины X — числа прочитанных за каникулы
- 9. Нужно сравнить интерес к чтению девочек и мальчиков этого класса. Для сравнения предложенных совокупностей могут быть
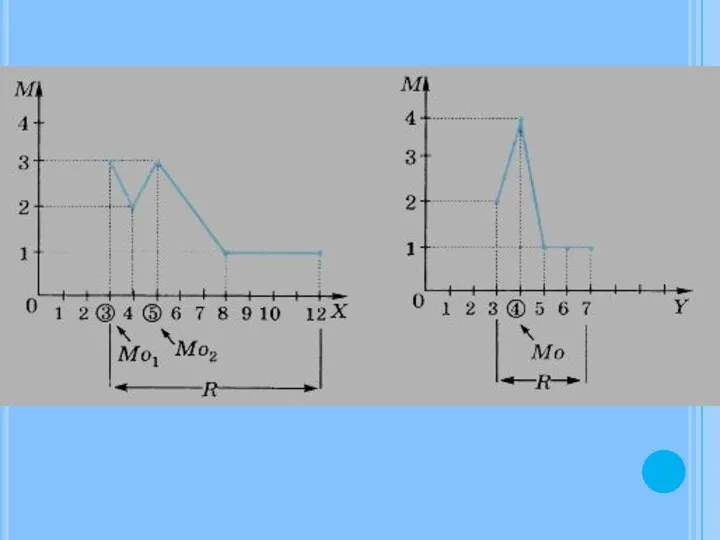
- 10. Размах (обозначается R) — разница между наибольшим и наименьшим значениями случайной величины. Мода (обозначим Мо) —
- 12. Пример 1. Вычислить размах, моду и медиану для последовательности: -2, 3, 4, -3, 0, 1, 3,
- 13. Средним значением случайной величины X (обозначается ) называют среднее арифметическое всех её значений. Если все значения
- 14. Если значения случайной величины Xl,Х2,...,Xk имеют в совокупности соответственно частоты М1,М2,…,Мk, то Зная, что , формулу
- 16. Скачать презентацию










 Математика и техника. Их связь и значение
Математика и техника. Их связь и значение Презентация на тему Что такое функция
Презентация на тему Что такое функция  МХСИ
МХСИ Переместительное свойство умножения
Переместительное свойство умножения Умножение на 1 и 0
Умножение на 1 и 0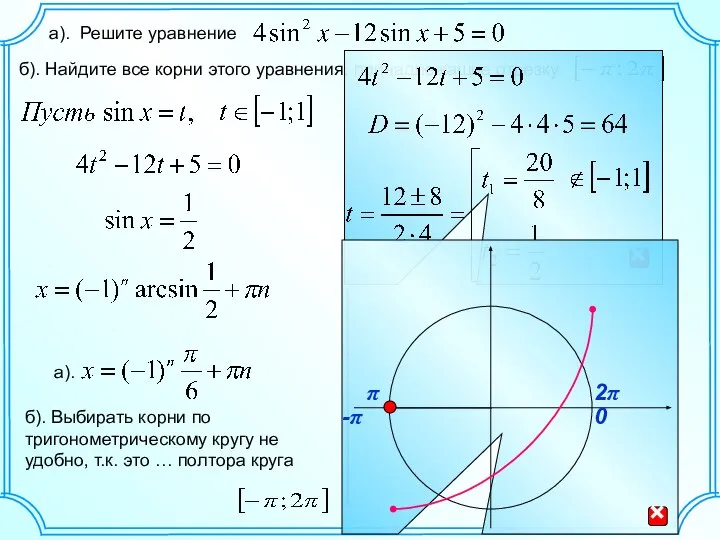 Решение уравнений C 22, по тригонометрии
Решение уравнений C 22, по тригонометрии Число и цифра 1. 1 класс
Число и цифра 1. 1 класс Математика ЕГЭ. Углы и прямые
Математика ЕГЭ. Углы и прямые Презентация на тему Диаграммы (6 класс)
Презентация на тему Диаграммы (6 класс)  Образование чисел, которые больше 20
Образование чисел, которые больше 20 Конструктивная геометрия. Лекция 5. Метрические задачи
Конструктивная геометрия. Лекция 5. Метрические задачи Неполные квадратные уравнения
Неполные квадратные уравнения Геометрические портреты
Геометрические портреты Предмет математика. Счёт предметов. Один, два, три…
Предмет математика. Счёт предметов. Один, два, три… Комбинаторные задачи
Комбинаторные задачи Треугольник. Классификация треугольников
Треугольник. Классификация треугольников Задачи и примеры по математике
Задачи и примеры по математике Конкурс А ну-ка, математики!
Конкурс А ну-ка, математики! Устные упражнения по теме: корень п –ой степени
Устные упражнения по теме: корень п –ой степени Погрешности измерений
Погрешности измерений Первое знакомство с понятием вероятность. Урок 145
Первое знакомство с понятием вероятность. Урок 145 Числа и точки на прямой
Числа и точки на прямой Некоторые методические приемы для работы с детьми ЗПР на уроках математики
Некоторые методические приемы для работы с детьми ЗПР на уроках математики Зачем изучать математику?
Зачем изучать математику? Преобразование подобия
Преобразование подобия LP (1)
LP (1) Контрольная работа
Контрольная работа Подобные слагаемые
Подобные слагаемые