Содержание
- 2. Литература 1. Берман Г.Н. Циклоида. – М.: Наука, 1980. 2. Веров С. Касательные к рулеттам. –
- 3. Учебные пособия по наглядной геометрии для 5, 6 классов издательства «Мнемозина»
- 4. 6 класс 5 класс
- 5. Авторский сайт: vasmirnov.ru
- 6. Циклоида Одним из древнейших способов образования кривых является кинематический способ, при котором кривая получается как траектория
- 7. Первым, кто стал изучать циклоиду, был Галилео Галилей (1564–1642). Он же придумал и её название.
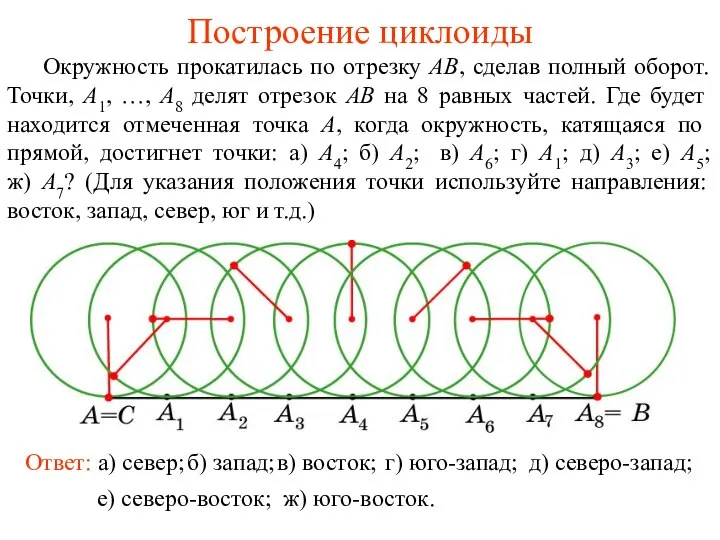
- 8. Построение циклоиды Окружность прокатилась по отрезку AB, сделав полный оборот. Точки, A1, …, A8 делят отрезок
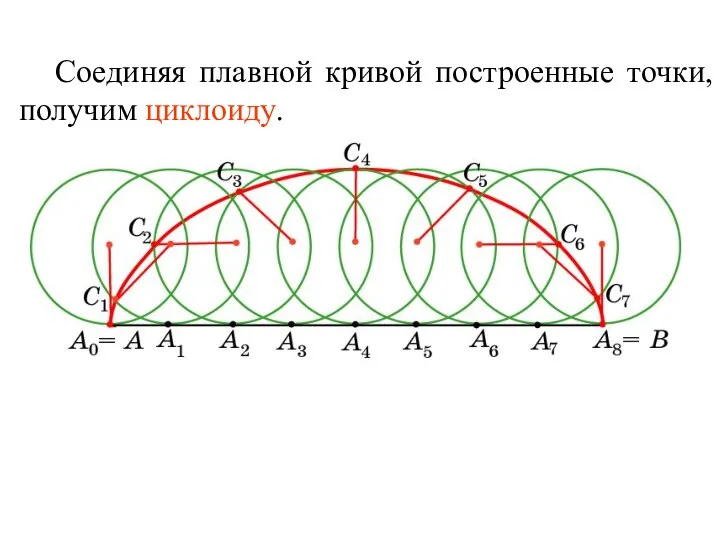
- 9. Соединяя плавной кривой построенные точки, получим циклоиду.
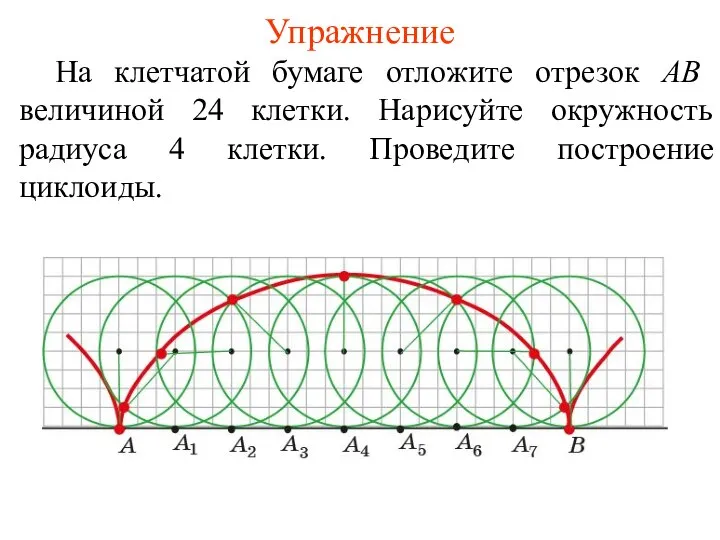
- 10. Упражнение На клетчатой бумаге отложите отрезок AB величиной 24 клетки. Нарисуйте окружность радиуса 4 клетки. Проведите
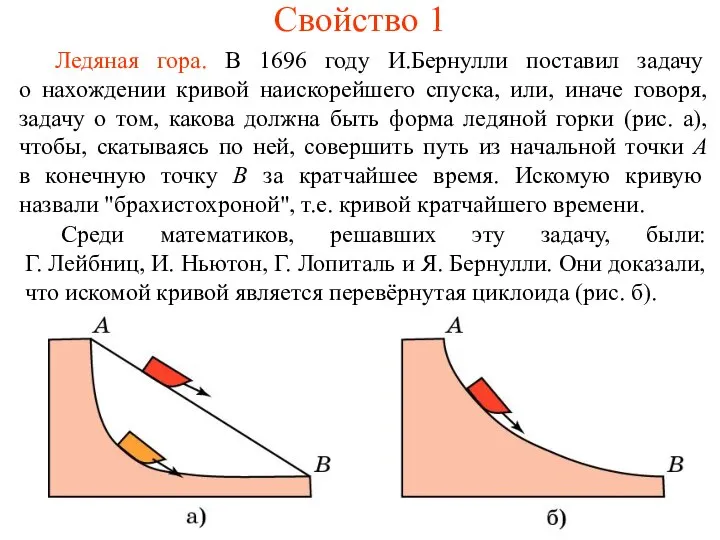
- 11. Свойство 1 Ледяная гора. В 1696 году И.Бернулли поставил задачу о нахождении кривой наискорейшего спуска, или,
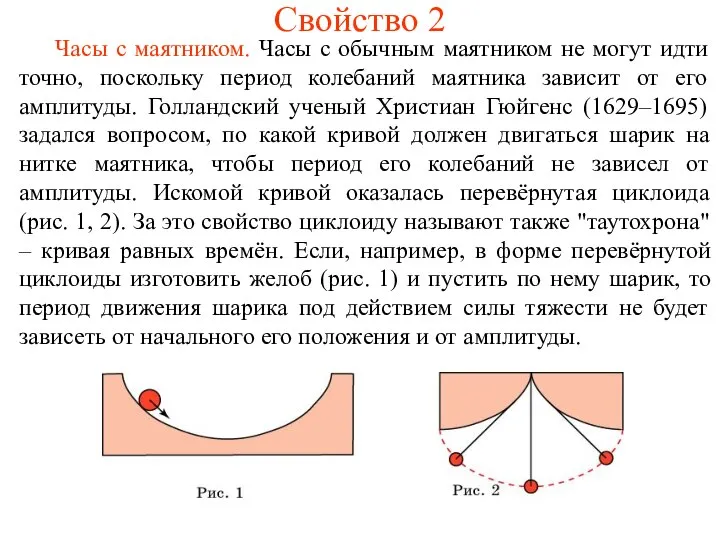
- 12. Свойство 2 Часы с маятником. Часы с обычным маятником не могут идти точно, поскольку период колебаний
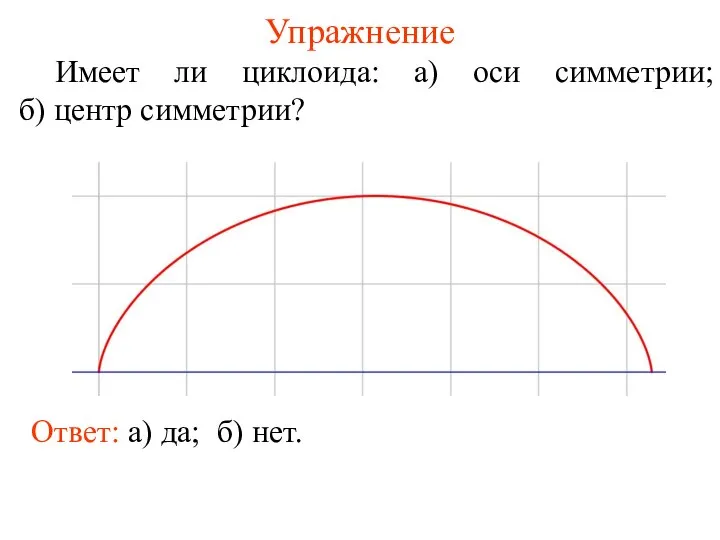
- 13. Упражнение Имеет ли циклоида: а) оси симметрии; б) центр симметрии? Ответ: а) да; б) нет.
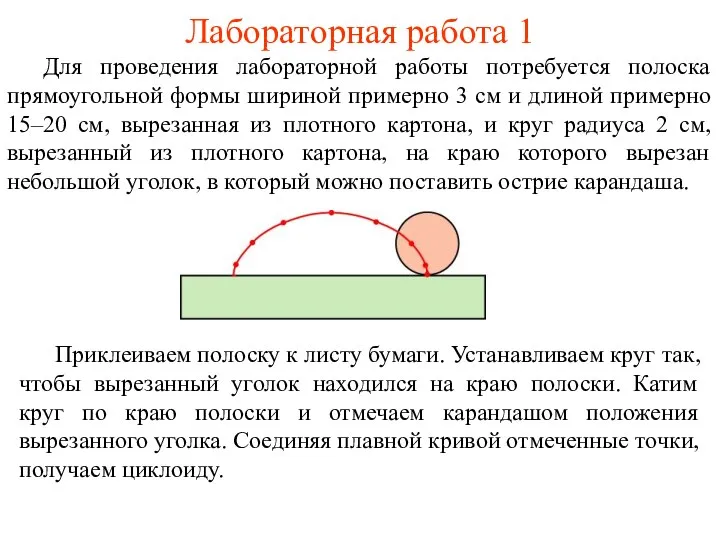
- 14. Лабораторная работа 1 Для проведения лабораторной работы потребуется полоска прямоугольной формы шириной примерно 3 см и
- 15. Лабораторная работа 2 Для получения циклоиды можно воспользоваться программой GeoGebra. Её рабочее окно показано на рисунке.
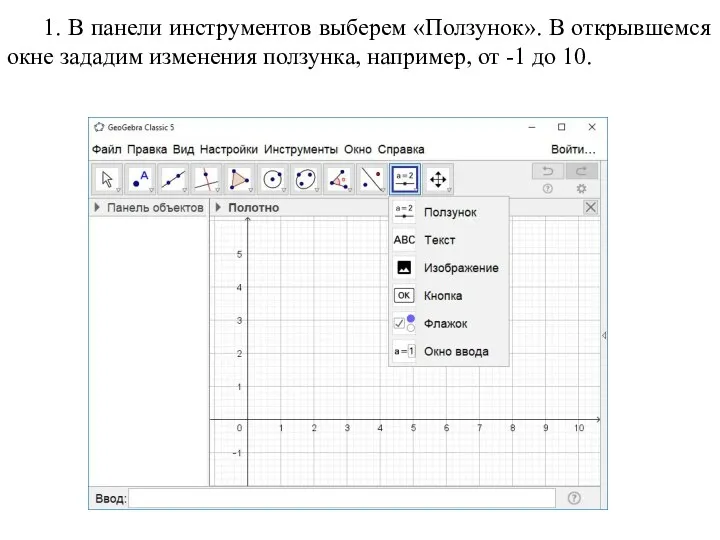
- 16. 1. В панели инструментов выберем «Ползунок». В открывшемся окне зададим изменения ползунка, например, от -1 до
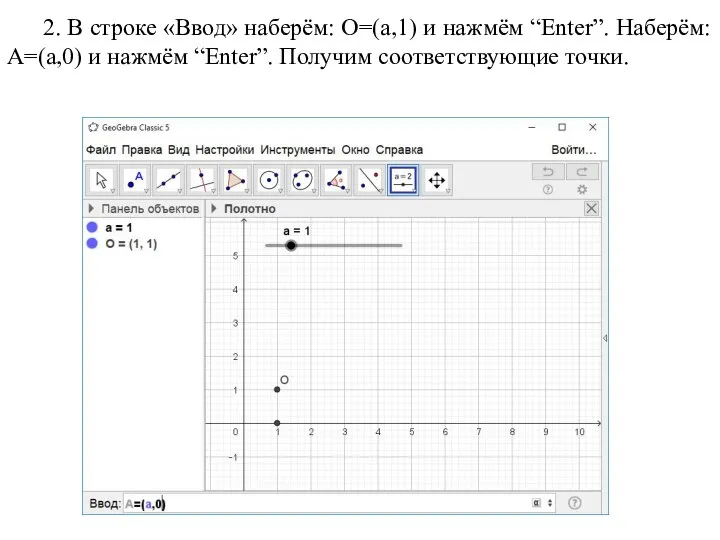
- 17. 2. В строке «Ввод» наберём: O=(a,1) и нажмём “Enter”. Наберём: A=(a,0) и нажмём “Enter”. Получим соответствующие
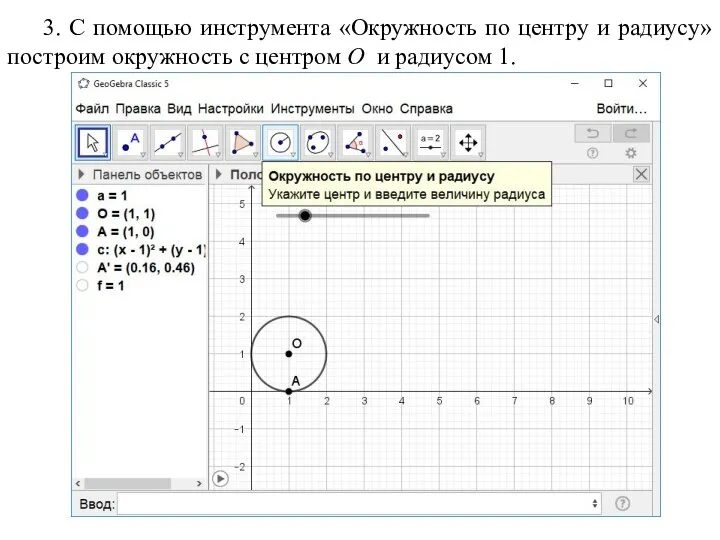
- 18. 3. С помощью инструмента «Окружность по центру и радиусу» построим окружность с центром O и радиусом
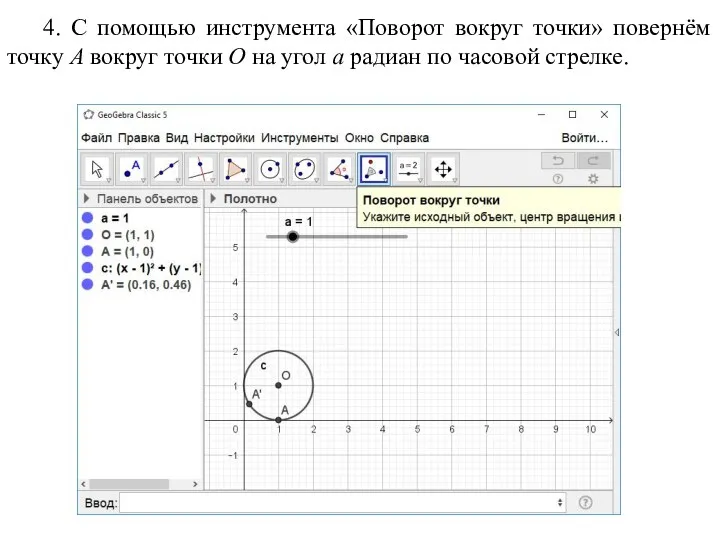
- 19. 4. С помощью инструмента «Поворот вокруг точки» повернём точку A вокруг точки O на угол a
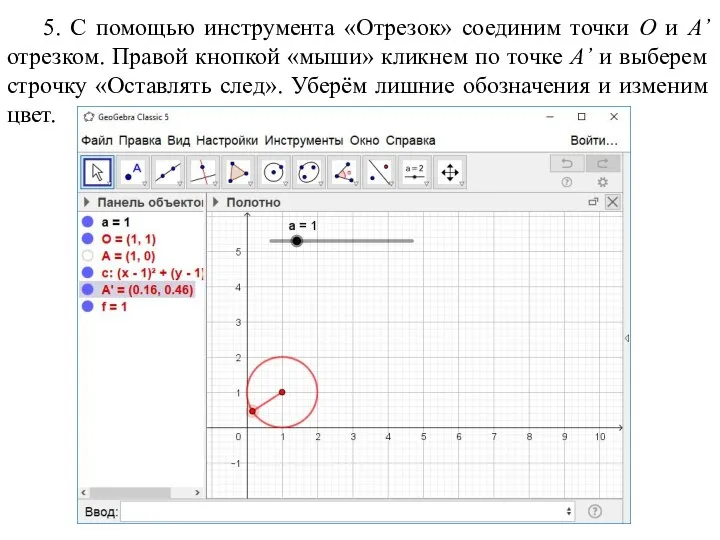
- 20. 5. С помощью инструмента «Отрезок» соединим точки O и A’ отрезком. Правой кнопкой «мыши» кликнем по
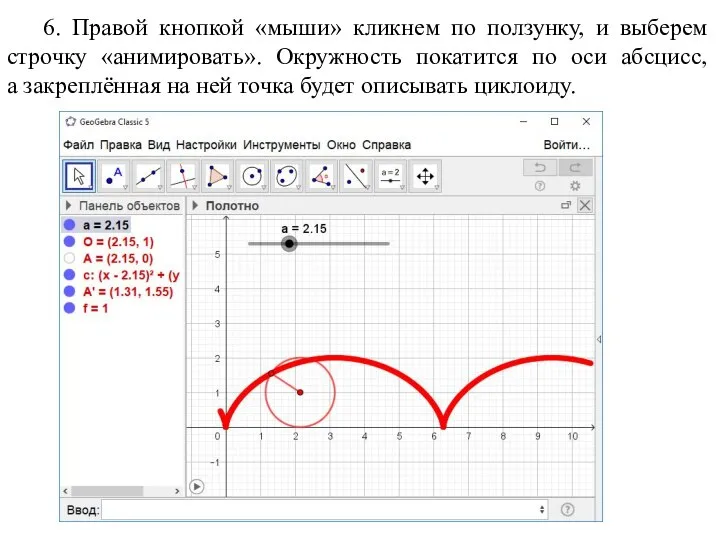
- 21. 6. Правой кнопкой «мыши» кликнем по ползунку, и выберем строчку «анимировать». Окружность покатится по оси абсцисс,
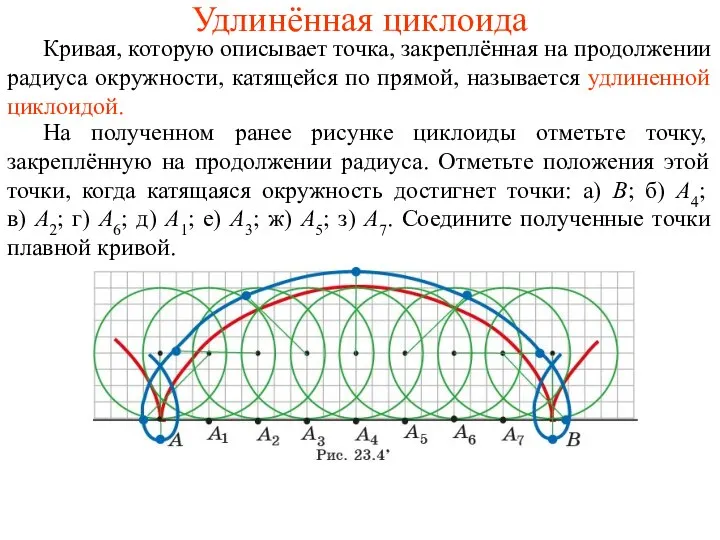
- 22. Удлинённая циклоида Кривая, которую описывает точка, закреплённая на продолжении радиуса окружности, катящейся по прямой, называется удлиненной
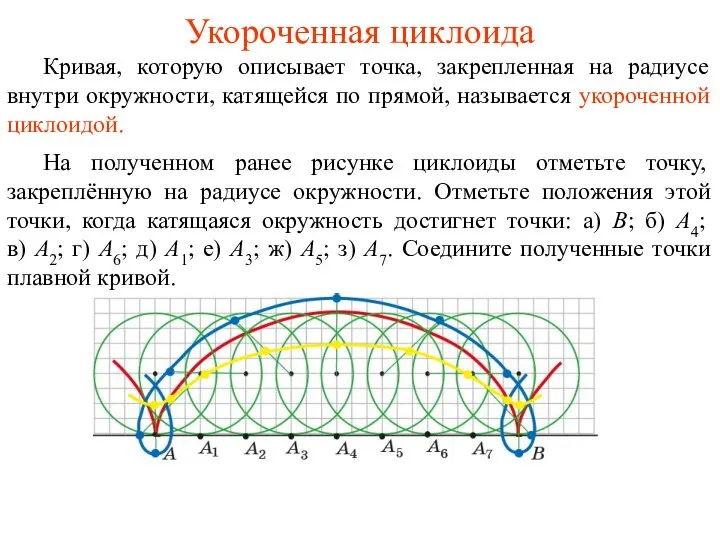
- 23. Укороченная циклоида Кривая, которую описывает точка, закрепленная на радиусе внутри окружности, катящейся по прямой, называется укороченной
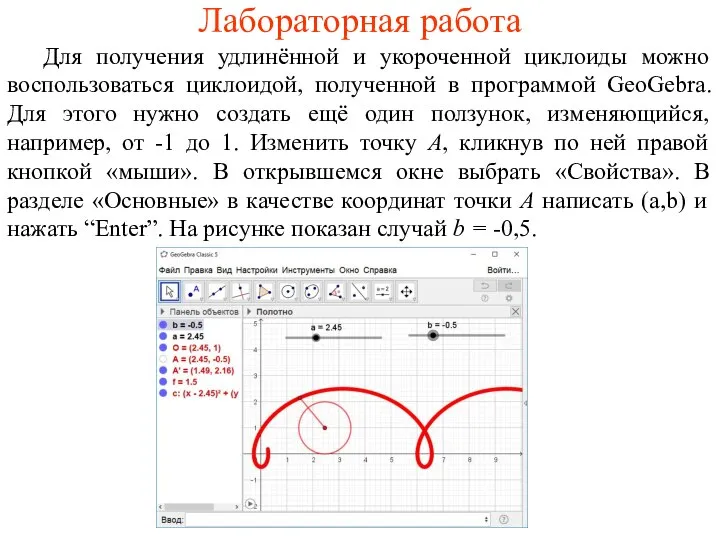
- 24. Лабораторная работа Для получения удлинённой и укороченной циклоиды можно воспользоваться циклоидой, полученной в программой GeoGebra. Для
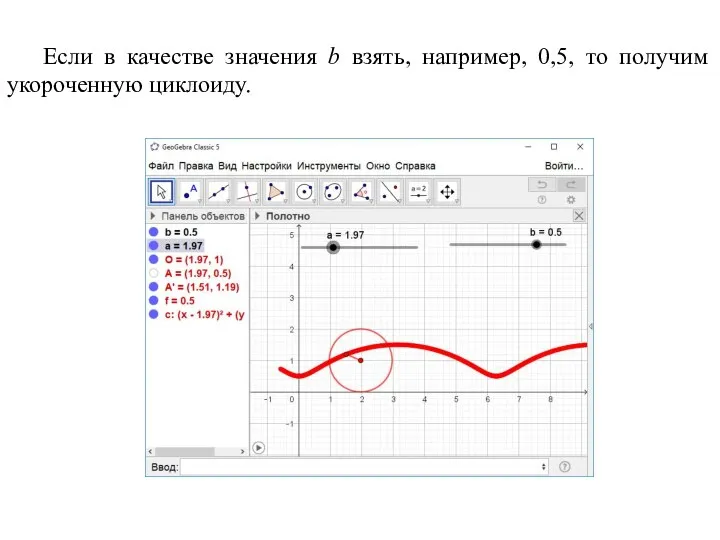
- 25. Если в качестве значения b взять, например, 0,5, то получим укороченную циклоиду.
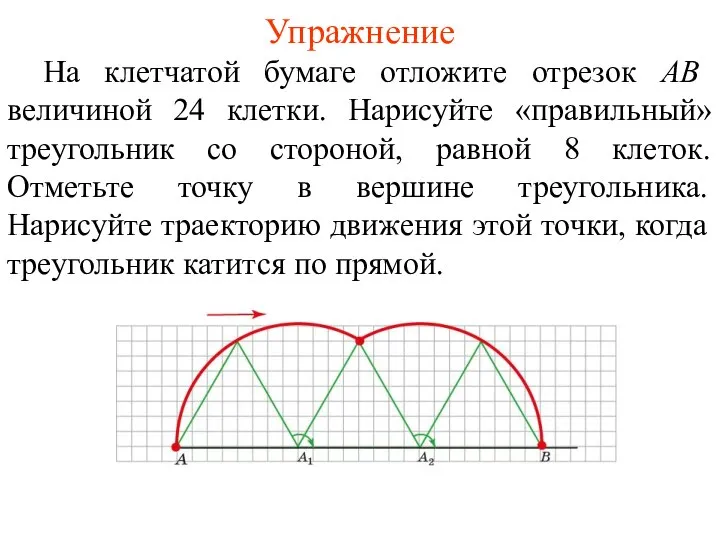
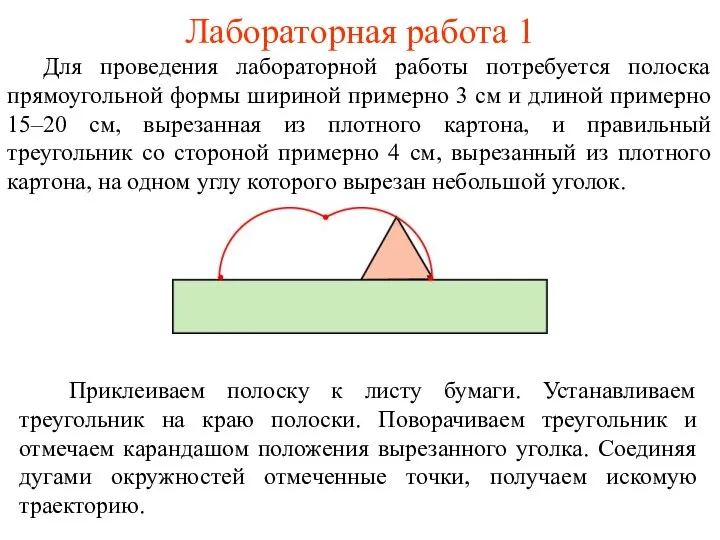
- 26. Упражнение На клетчатой бумаге отложите отрезок AB величиной 24 клетки. Нарисуйте «правильный» треугольник со стороной, равной
- 27. Лабораторная работа 1 Для проведения лабораторной работы потребуется полоска прямоугольной формы шириной примерно 3 см и
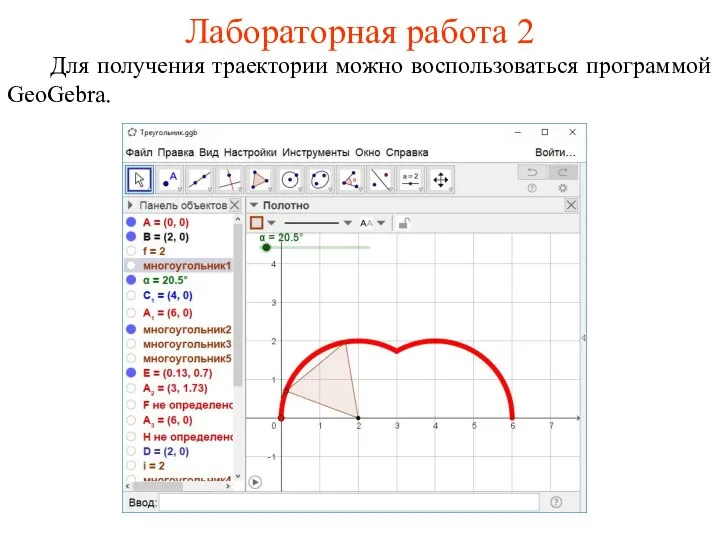
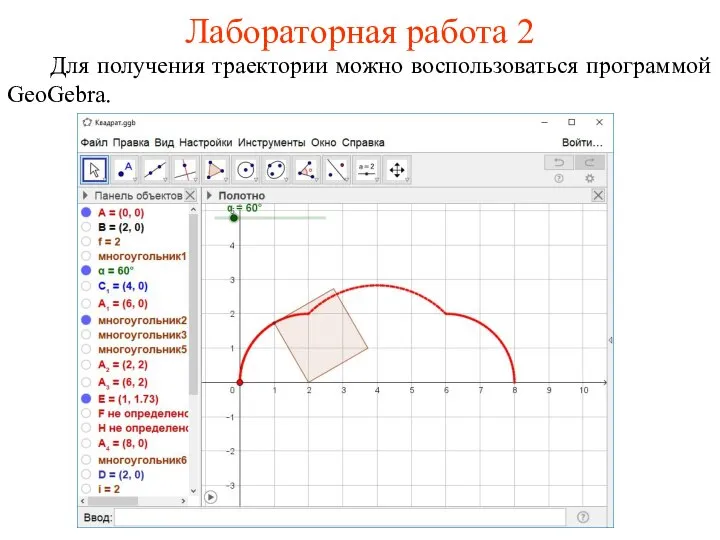
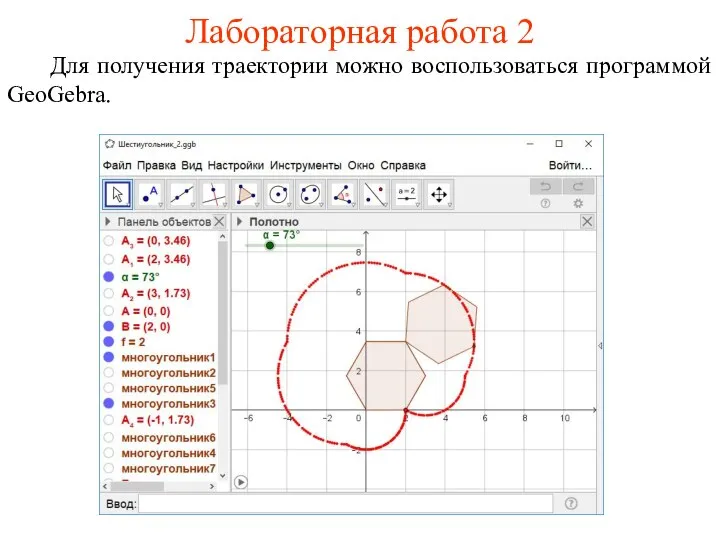
- 28. Лабораторная работа 2 Для получения траектории можно воспользоваться программой GeoGebra.
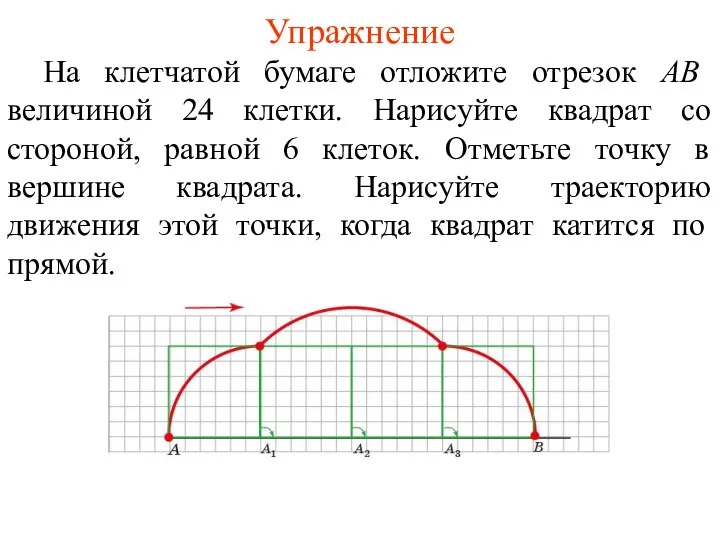
- 29. Упражнение На клетчатой бумаге отложите отрезок AB величиной 24 клетки. Нарисуйте квадрат со стороной, равной 6
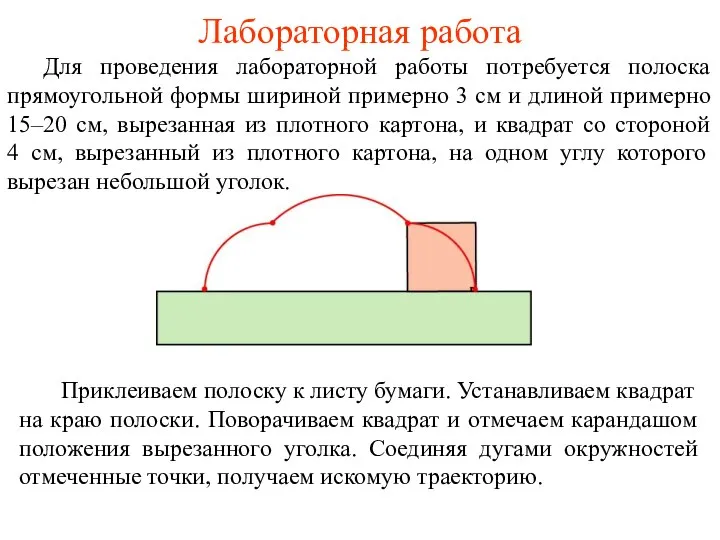
- 30. Лабораторная работа Для проведения лабораторной работы потребуется полоска прямоугольной формы шириной примерно 3 см и длиной
- 31. Лабораторная работа 2 Для получения траектории можно воспользоваться программой GeoGebra.
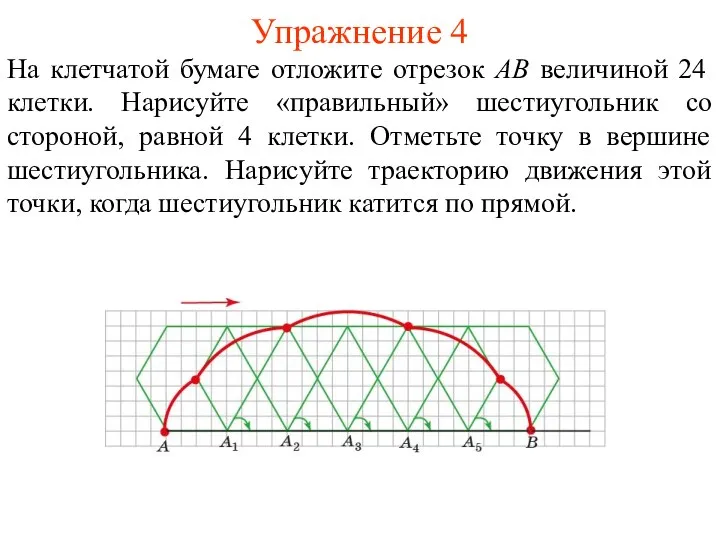
- 32. Упражнение 4 На клетчатой бумаге отложите отрезок AB величиной 24 клетки. Нарисуйте «правильный» шестиугольник со стороной,
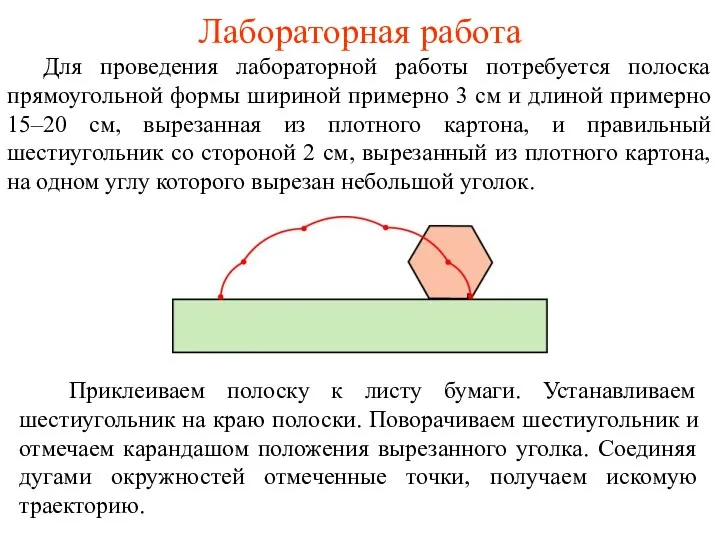
- 33. Лабораторная работа Для проведения лабораторной работы потребуется полоска прямоугольной формы шириной примерно 3 см и длиной
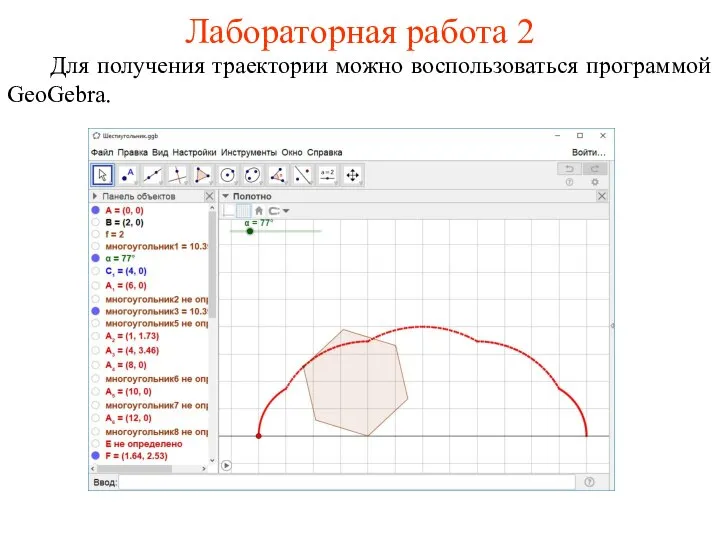
- 34. Лабораторная работа 2 Для получения траектории можно воспользоваться программой GeoGebra.
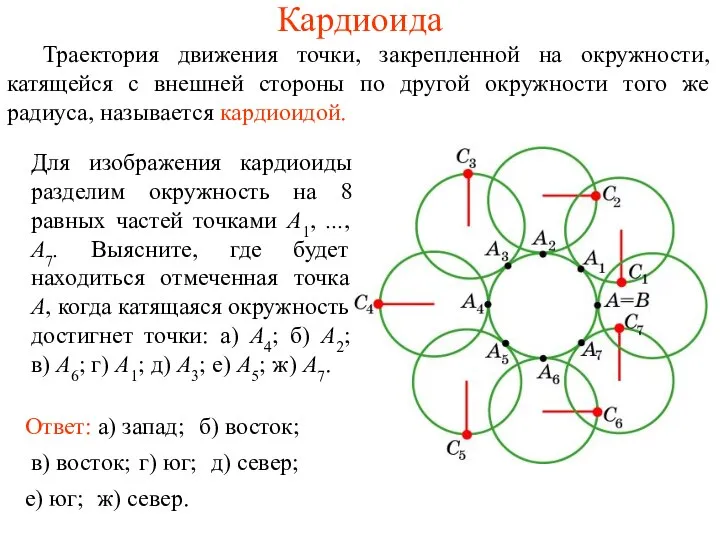
- 35. Кардиоида Траектория движения точки, закрепленной на окружности, катящейся с внешней стороны по другой окружности того же
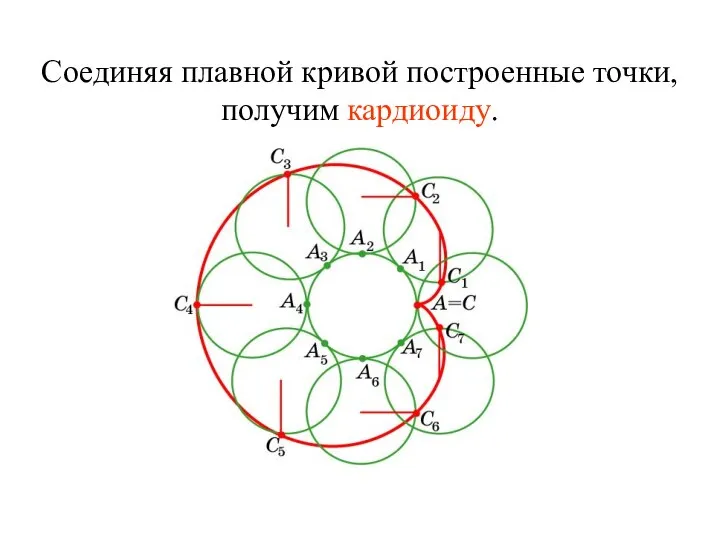
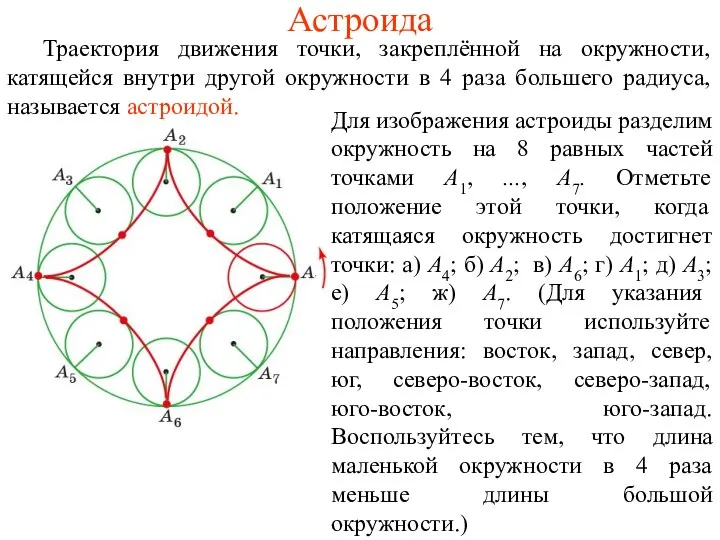
- 36. Соединяя плавной кривой построенные точки, получим кардиоиду.
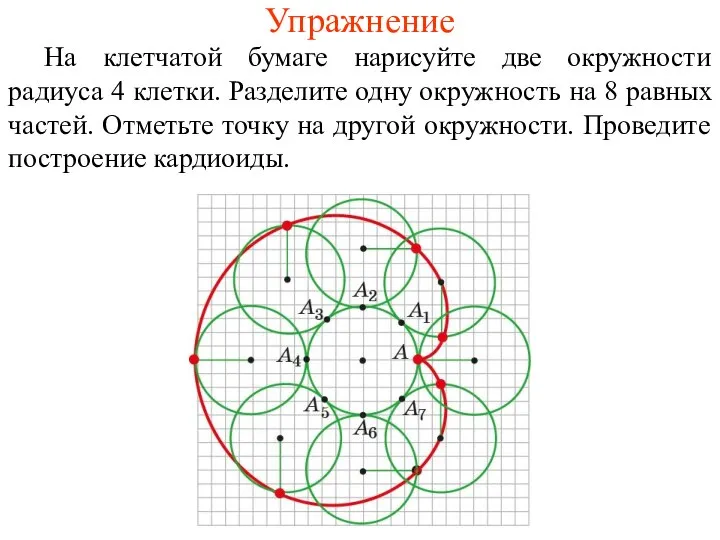
- 37. Упражнение На клетчатой бумаге нарисуйте две окружности радиуса 4 клетки. Разделите одну окружность на 8 равных
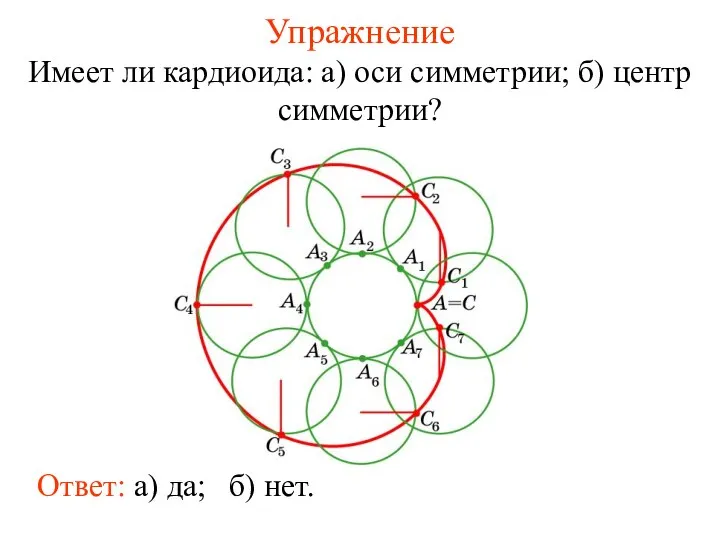
- 38. Упражнение Имеет ли кардиоида: а) оси симметрии; б) центр симметрии? Ответ: а) да; б) нет.
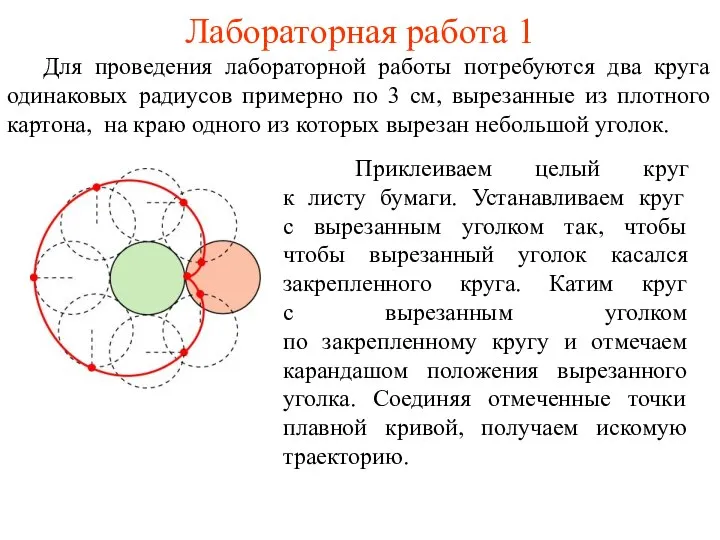
- 39. Лабораторная работа 1 Для проведения лабораторной работы потребуются два круга одинаковых радиусов примерно по 3 см,
- 40. Лабораторная работа 2 Для получения кардиоиды можно воспользоваться программой GeoGebra. Для этого в строке «Ввод» наберём:
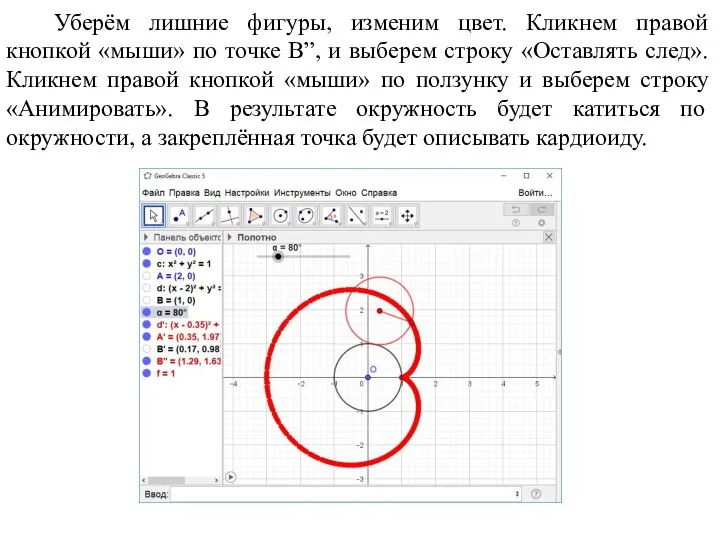
- 42. Уберём лишние фигуры, изменим цвет. Кликнем правой кнопкой «мыши» по точке B”, и выберем строку «Оставлять
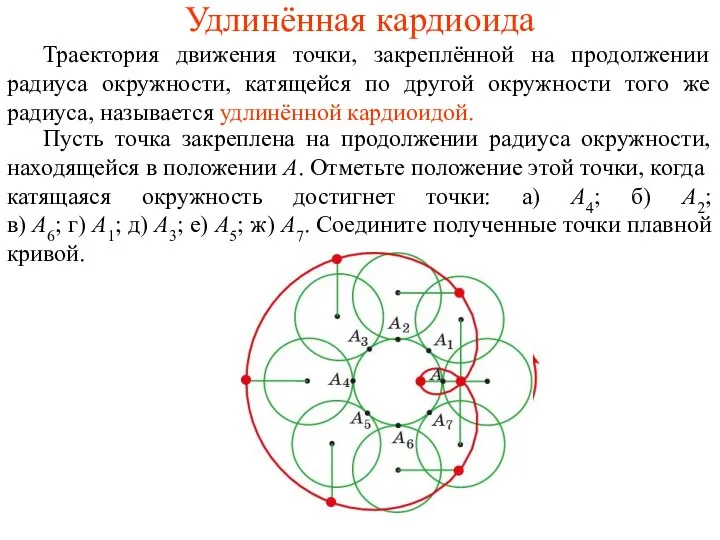
- 43. Удлинённая кардиоида Траектория движения точки, закреплённой на продолжении радиуса окружности, катящейся по другой окружности того же
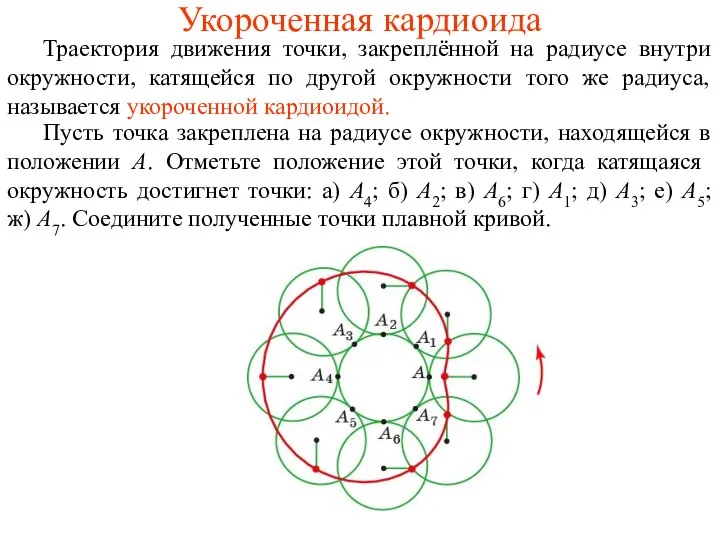
- 44. Укороченная кардиоида Траектория движения точки, закреплённой на радиусе внутри окружности, катящейся по другой окружности того же
- 45. Лабораторная работа Для получения удлинённой и укороченной кардиоиды можно воспользоваться ранее полученной кардиодой в программе GeoGebra.
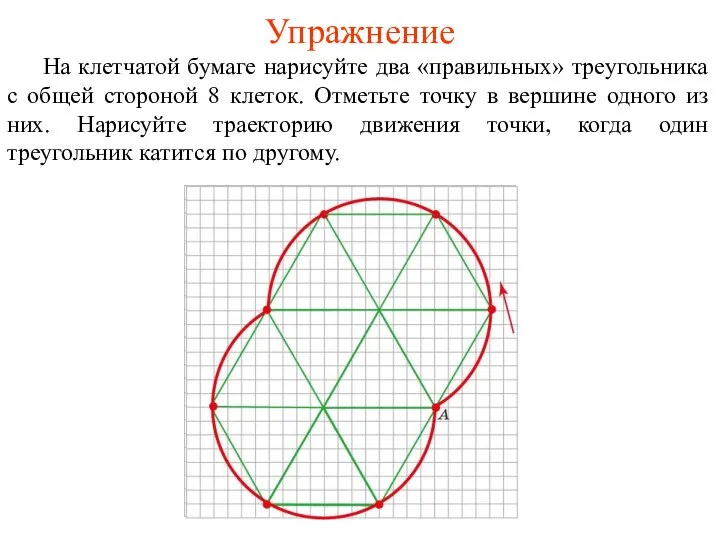
- 46. Упражнение На клетчатой бумаге нарисуйте два «правильных» треугольника с общей стороной 8 клеток. Отметьте точку в
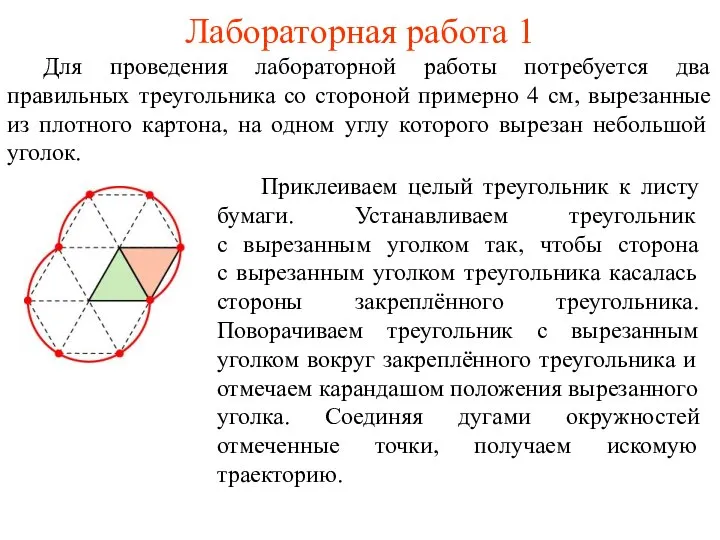
- 47. Лабораторная работа 1 Для проведения лабораторной работы потребуется два правильных треугольника со стороной примерно 4 см,
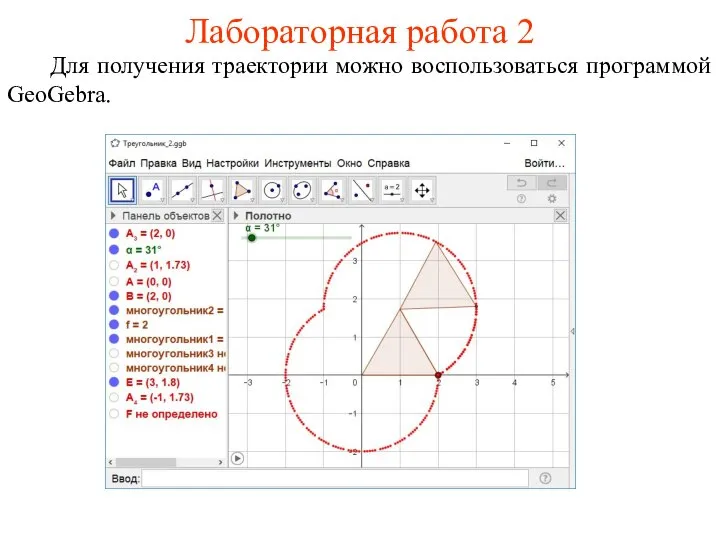
- 48. Лабораторная работа 2 Для получения траектории можно воспользоваться программой GeoGebra.
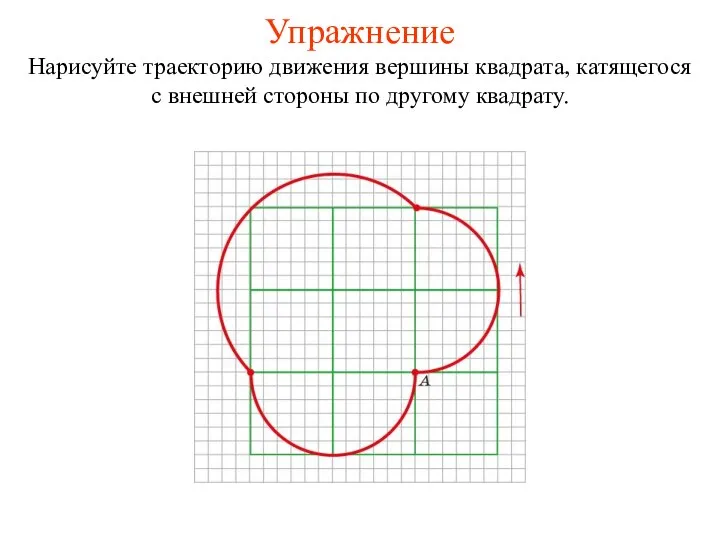
- 49. Упражнение Нарисуйте траекторию движения вершины квадрата, катящегося с внешней стороны по другому квадрату.
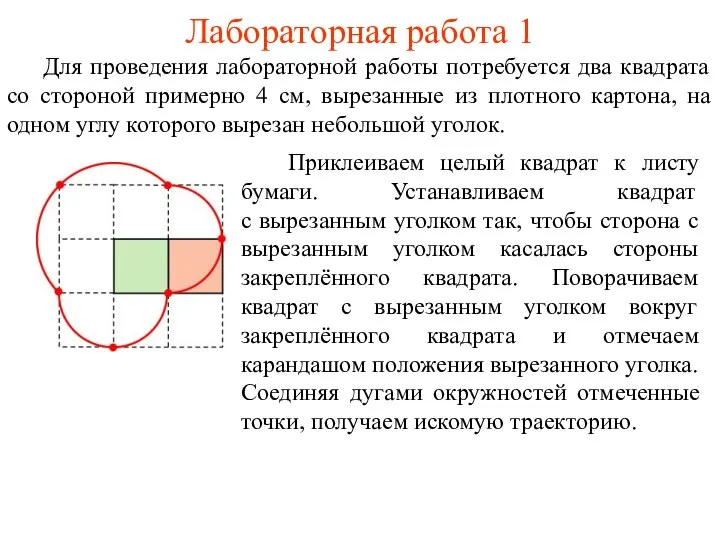
- 50. Лабораторная работа 1 Для проведения лабораторной работы потребуется два квадрата со стороной примерно 4 см, вырезанные
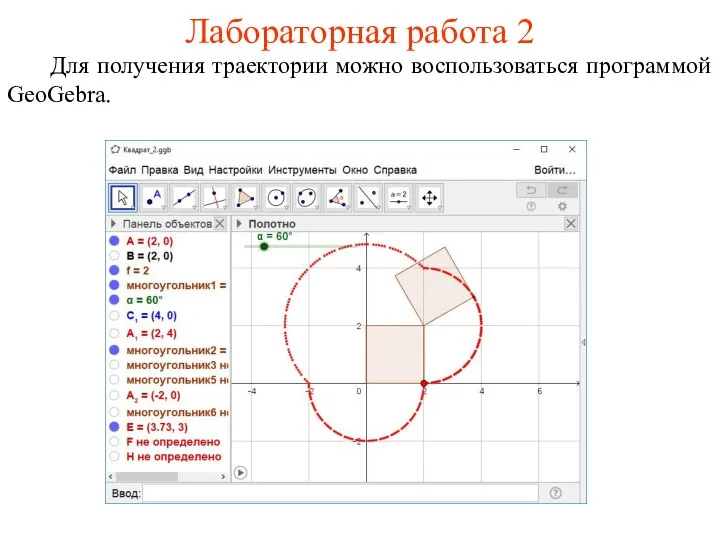
- 51. Лабораторная работа 2 Для получения траектории можно воспользоваться программой GeoGebra.
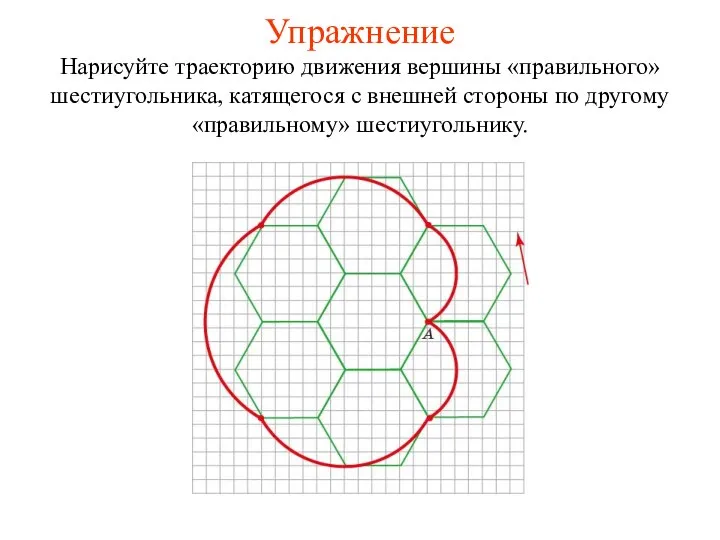
- 52. Упражнение Нарисуйте траекторию движения вершины «правильного» шестиугольника, катящегося с внешней стороны по другому «правильному» шестиугольнику.
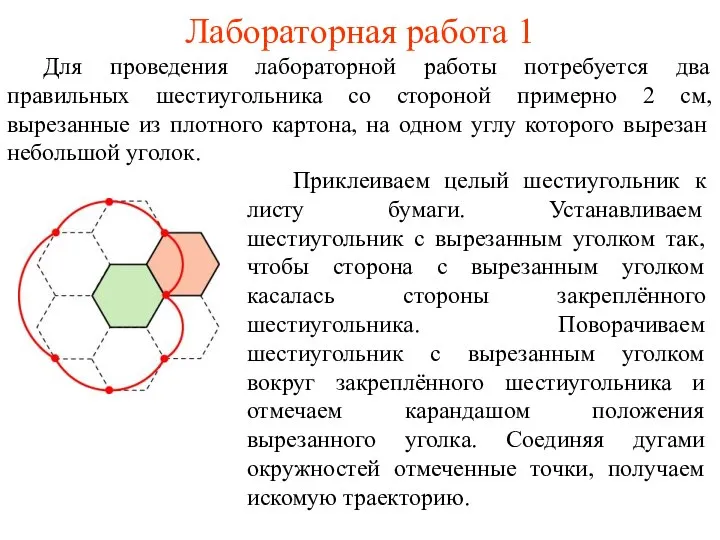
- 53. Лабораторная работа 1 Для проведения лабораторной работы потребуется два правильных шестиугольника со стороной примерно 2 см,
- 54. Лабораторная работа 2 Для получения траектории можно воспользоваться программой GeoGebra.
- 55. Астроида Траектория движения точки, закреплённой на окружности, катящейся внутри другой окружности в 4 раза большего радиуса,
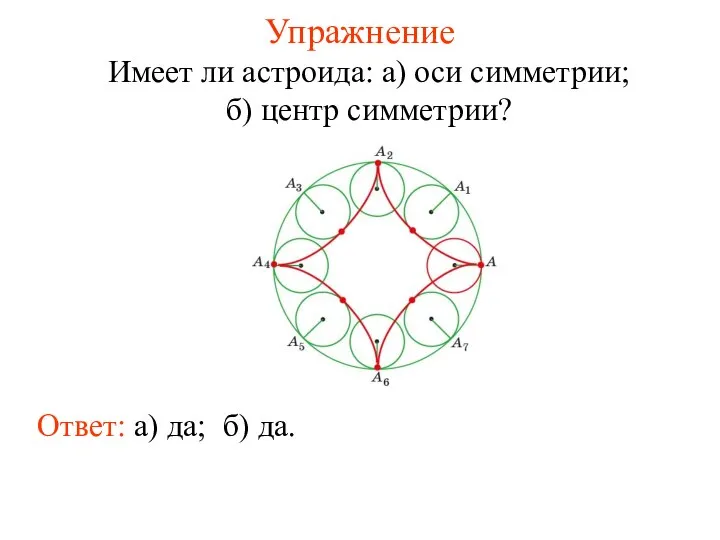
- 56. Упражнение Имеет ли астроида: а) оси симметрии; б) центр симметрии? Ответ: а) да; б) да.
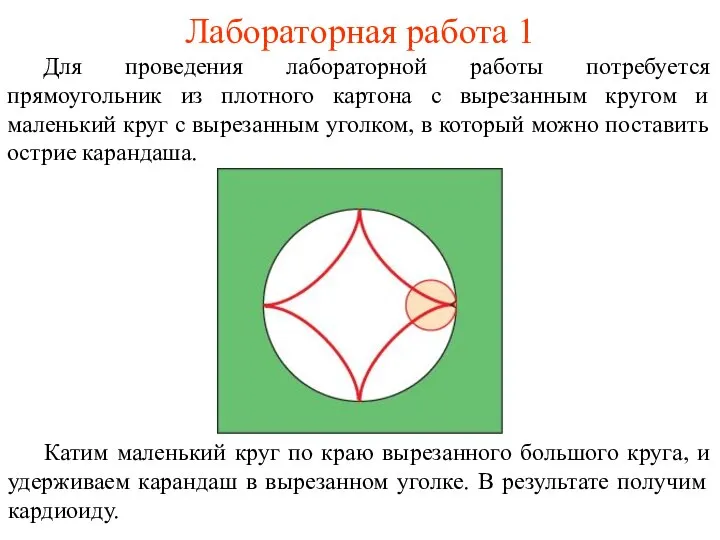
- 57. Лабораторная работа 1 Для проведения лабораторной работы потребуется прямоугольник из плотного картона с вырезанным кругом и
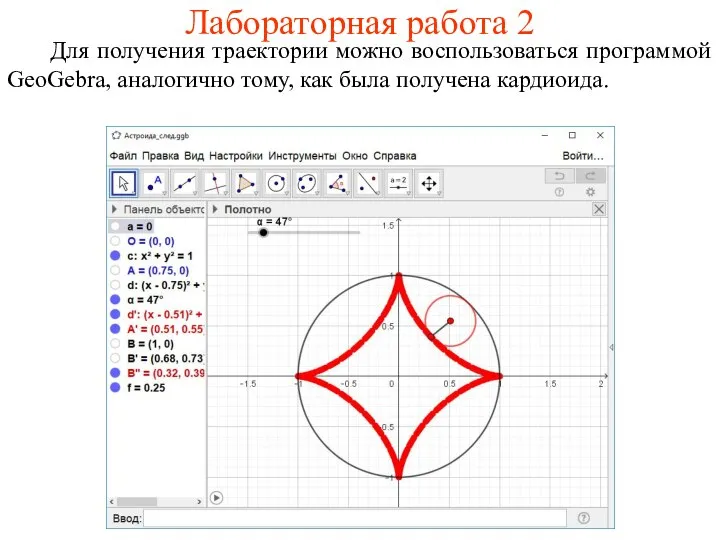
- 58. Лабораторная работа 2 Для получения траектории можно воспользоваться программой GeoGebra, аналогично тому, как была получена кардиоида.
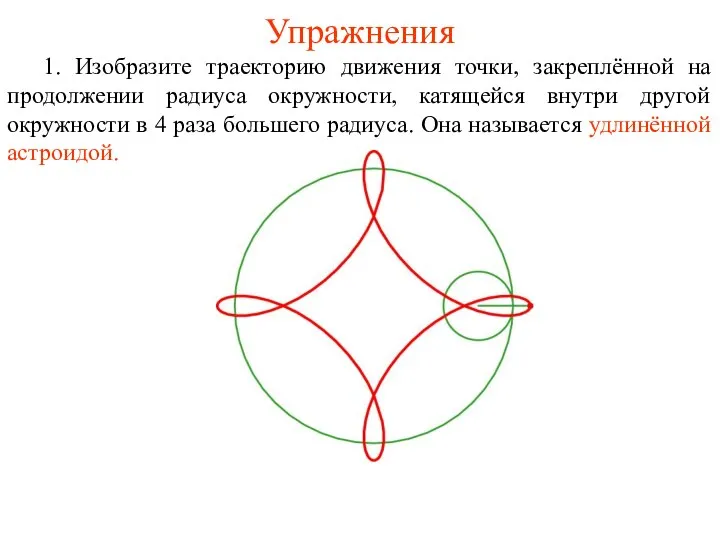
- 59. 1. Изобразите траекторию движения точки, закреплённой на продолжении радиуса окружности, катящейся внутри другой окружности в 4
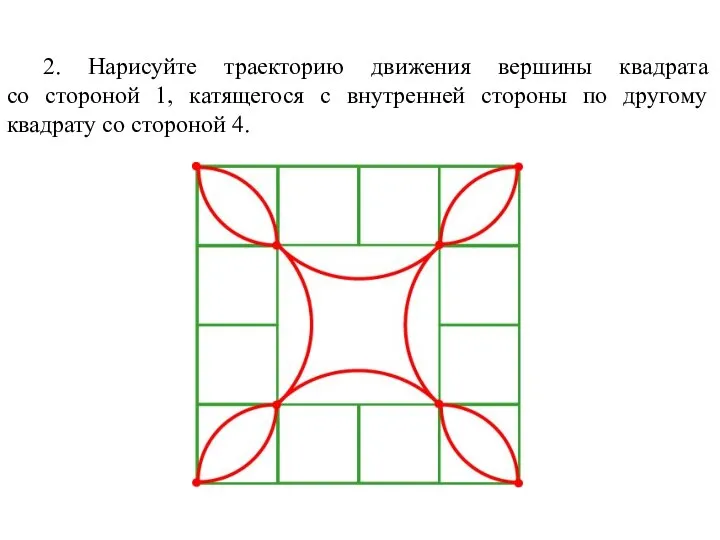
- 60. 2. Нарисуйте траекторию движения вершины квадрата со стороной 1, катящегося с внутренней стороны по другому квадрату
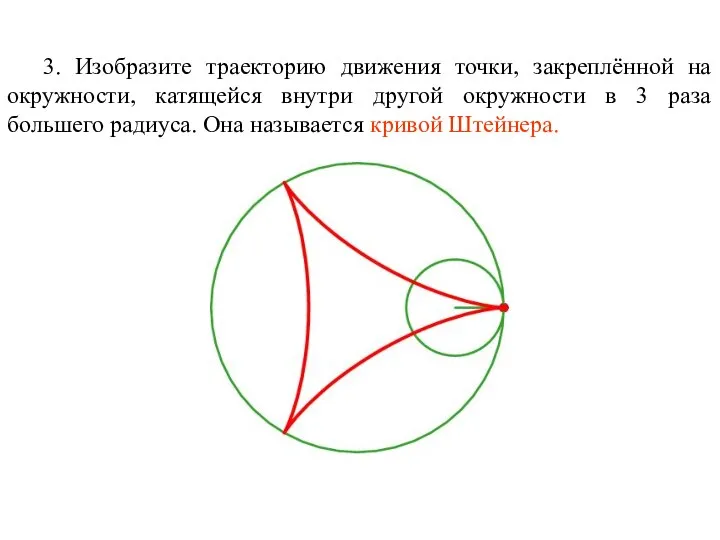
- 61. 3. Изобразите траекторию движения точки, закреплённой на окружности, катящейся внутри другой окружности в 3 раза большего
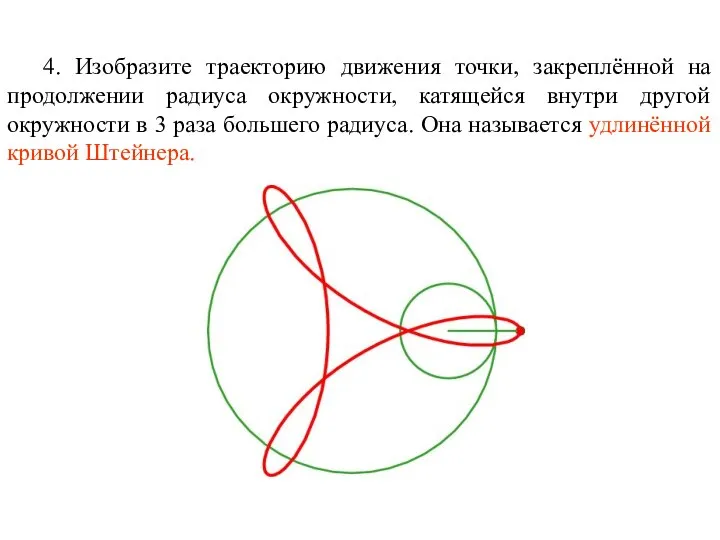
- 62. 4. Изобразите траекторию движения точки, закреплённой на продолжении радиуса окружности, катящейся внутри другой окружности в 3
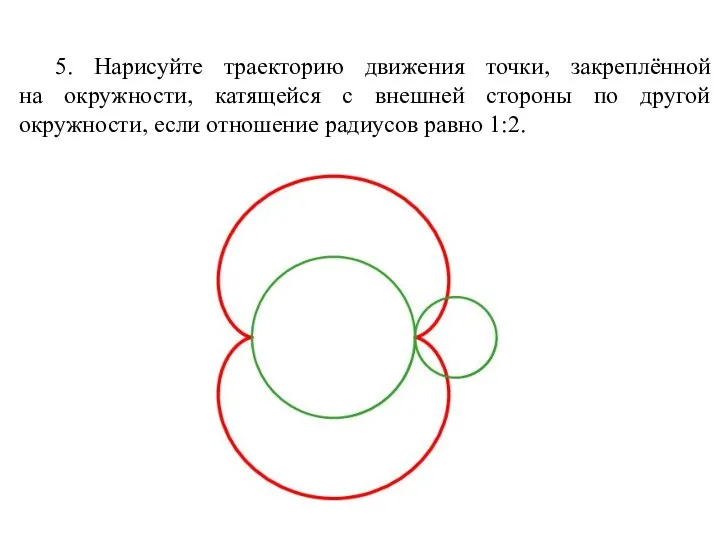
- 63. 5. Нарисуйте траекторию движения точки, закреплённой на окружности, катящейся с внешней стороны по другой окружности, если
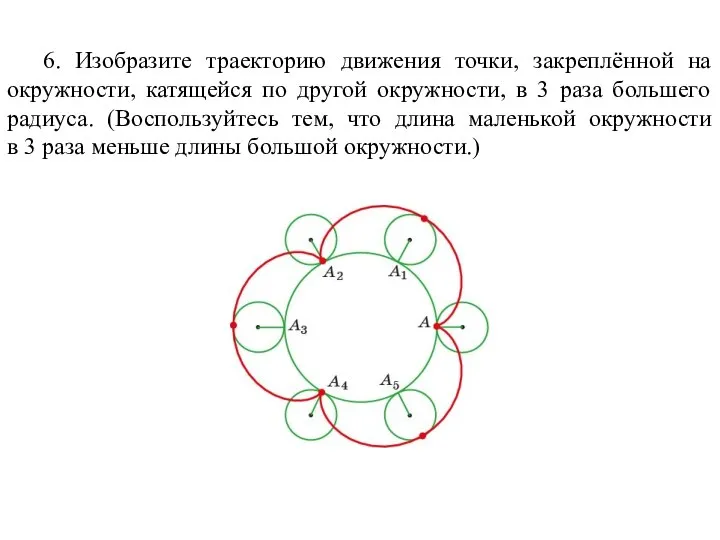
- 64. 6. Изобразите траекторию движения точки, закреплённой на окружности, катящейся по другой окружности, в 3 раза большего
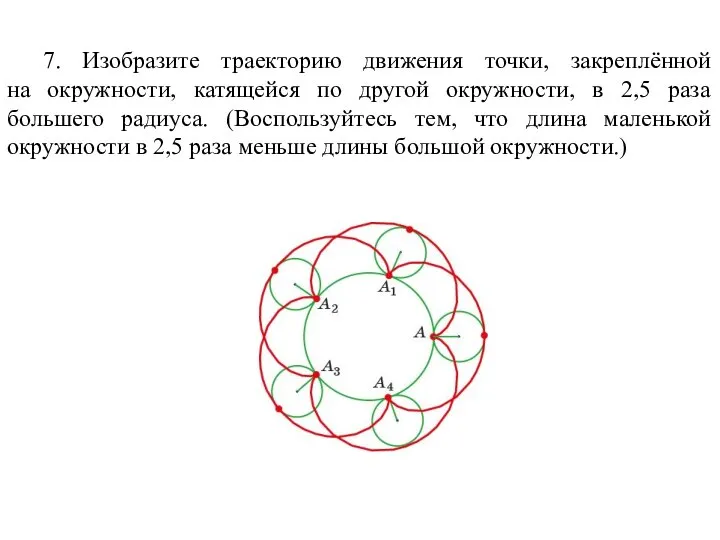
- 65. 7. Изобразите траекторию движения точки, закреплённой на окружности, катящейся по другой окружности, в 2,5 раза большего
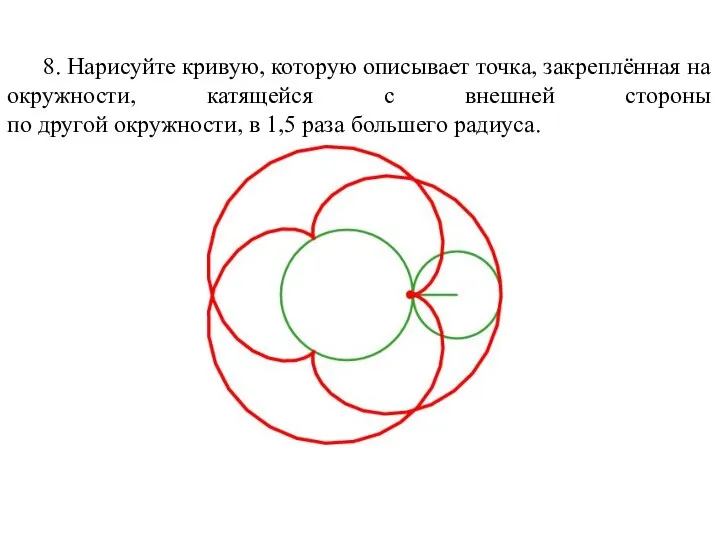
- 66. 8. Нарисуйте кривую, которую описывает точка, закреплённая на окружности, катящейся с внешней стороны по другой окружности,
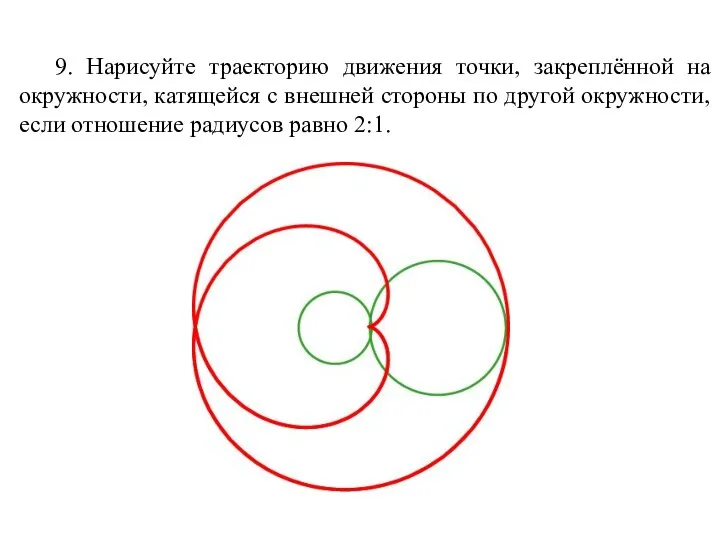
- 67. 9. Нарисуйте траекторию движения точки, закреплённой на окружности, катящейся с внешней стороны по другой окружности, если
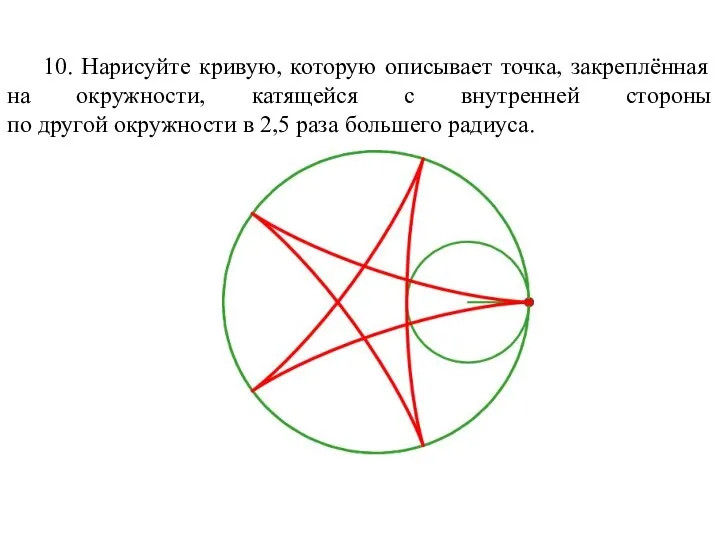
- 68. 10. Нарисуйте кривую, которую описывает точка, закреплённая на окружности, катящейся с внутренней стороны по другой окружности
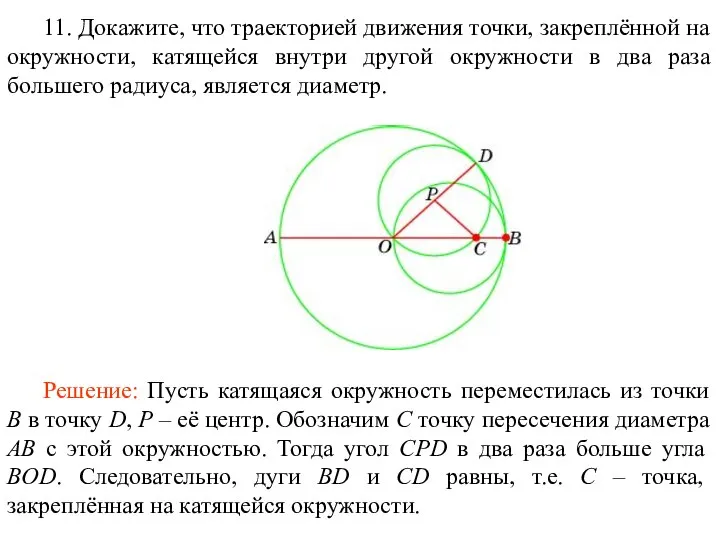
- 69. 11. Докажите, что траекторией движения точки, закреплённой на окружности, катящейся внутри другой окружности в два раза
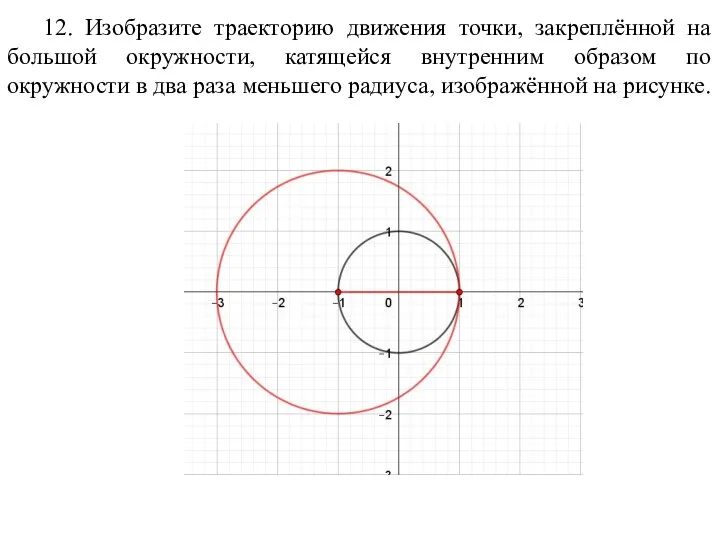
- 70. 12. Изобразите траекторию движения точки, закреплённой на большой окружности, катящейся внутренним образом по окружности в два
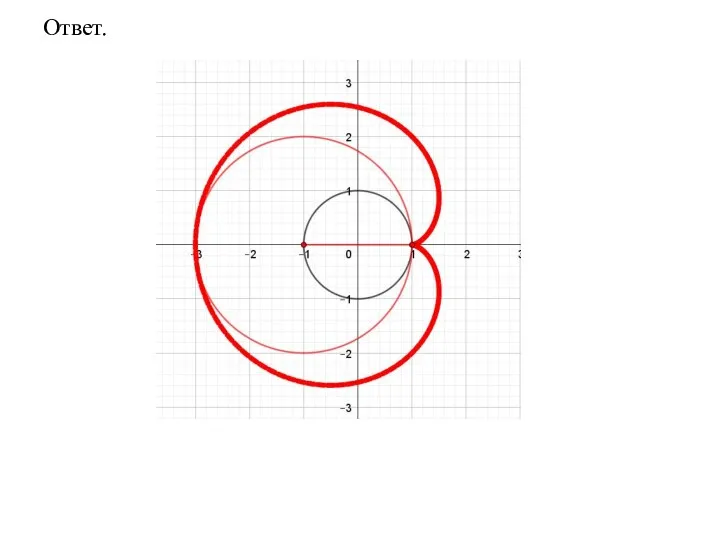
- 71. Ответ.
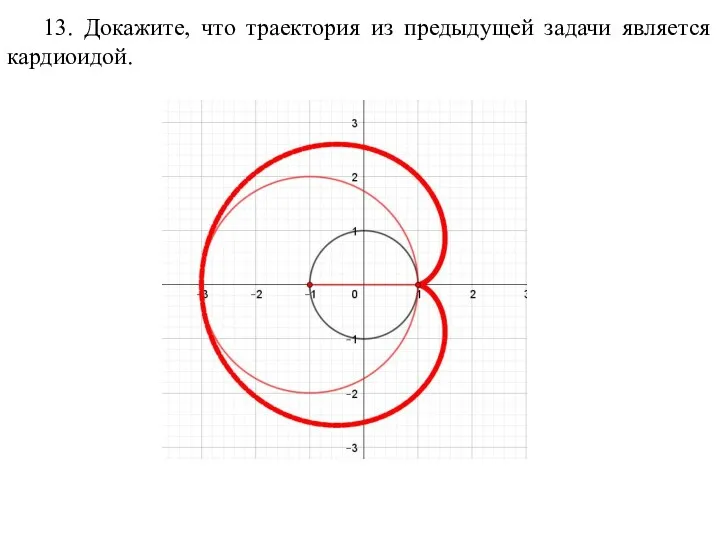
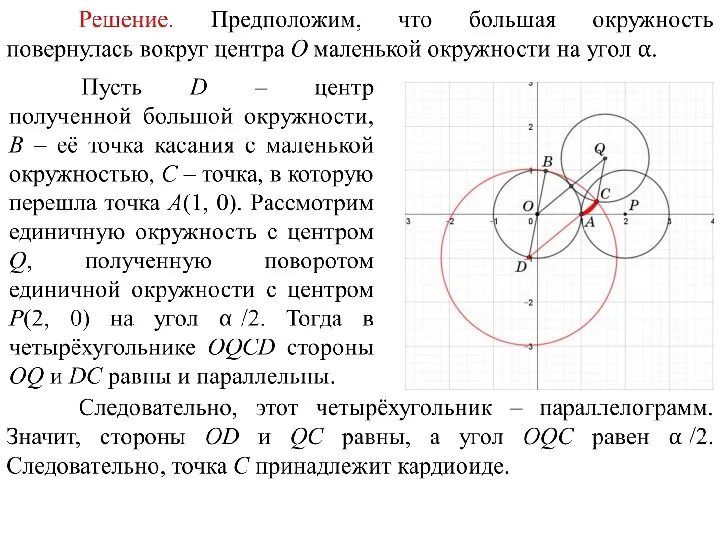
- 72. 13. Докажите, что траектория из предыдущей задачи является кардиоидой.
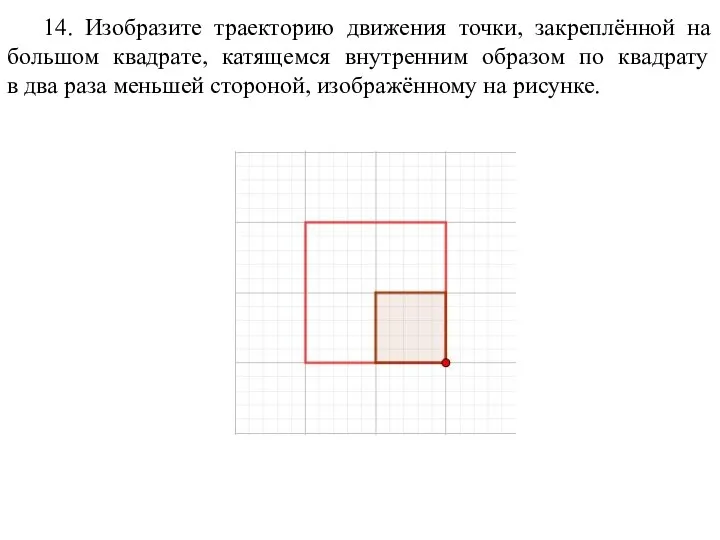
- 74. 14. Изобразите траекторию движения точки, закреплённой на большом квадрате, катящемся внутренним образом по квадрату в два
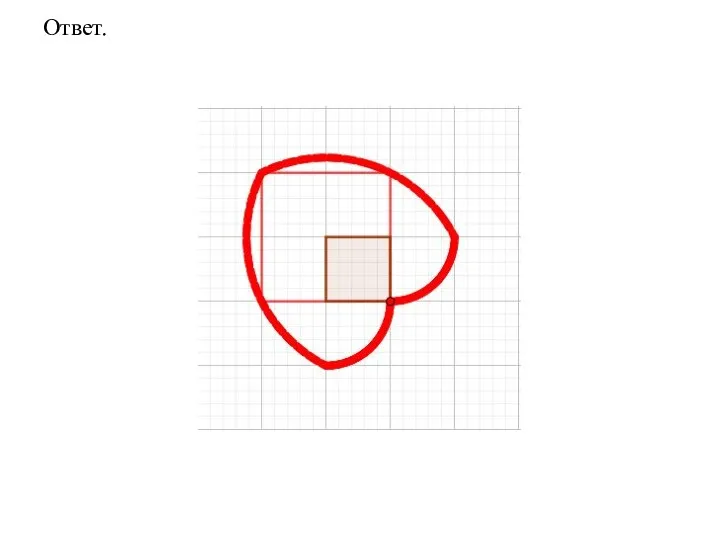
- 75. Ответ.
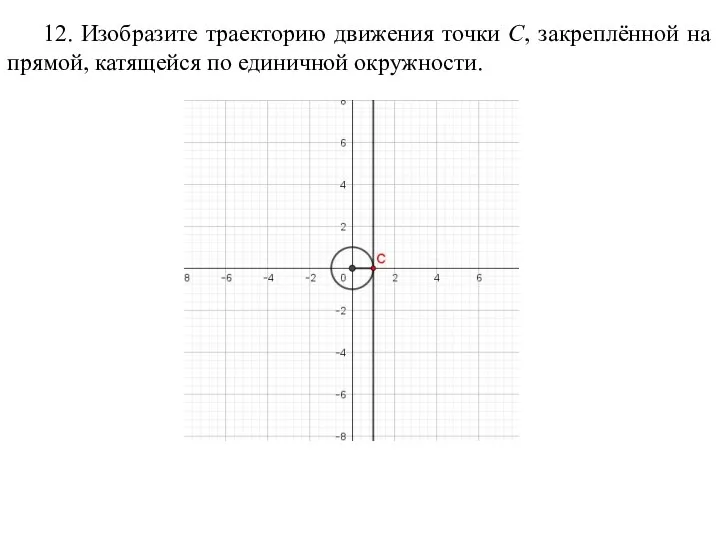
- 76. 12. Изобразите траекторию движения точки C, закреплённой на прямой, катящейся по единичной окружности.
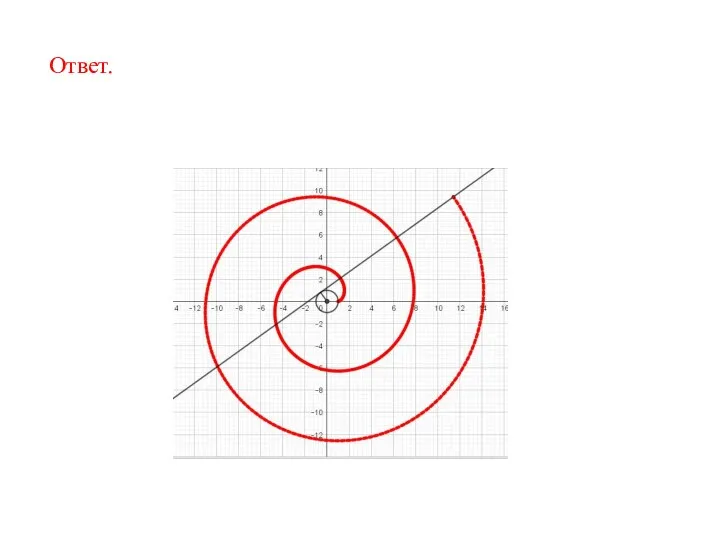
- 77. Ответ.
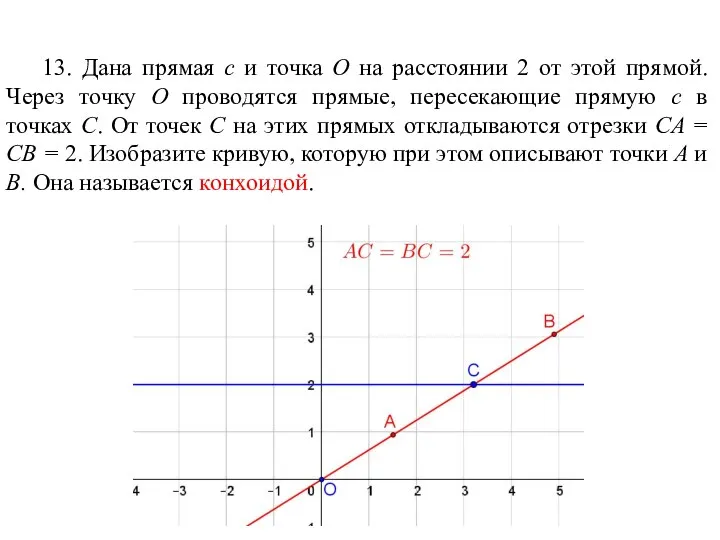
- 78. 13. Дана прямая c и точка O на расстоянии 2 от этой прямой. Через точку O
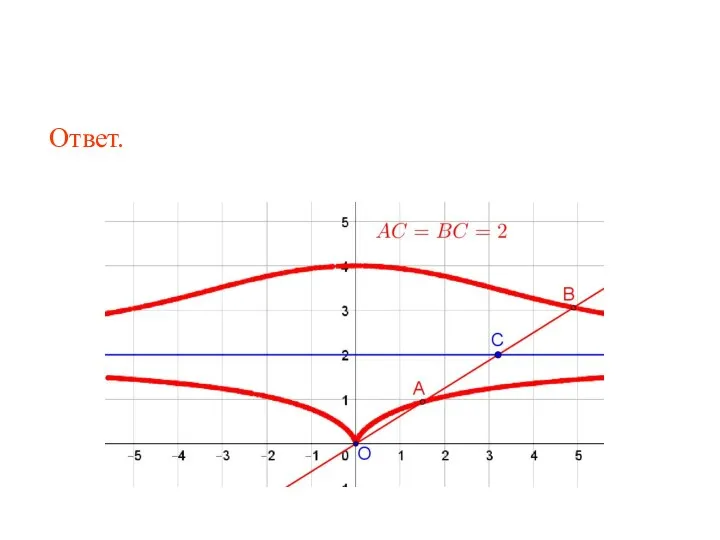
- 79. Ответ.
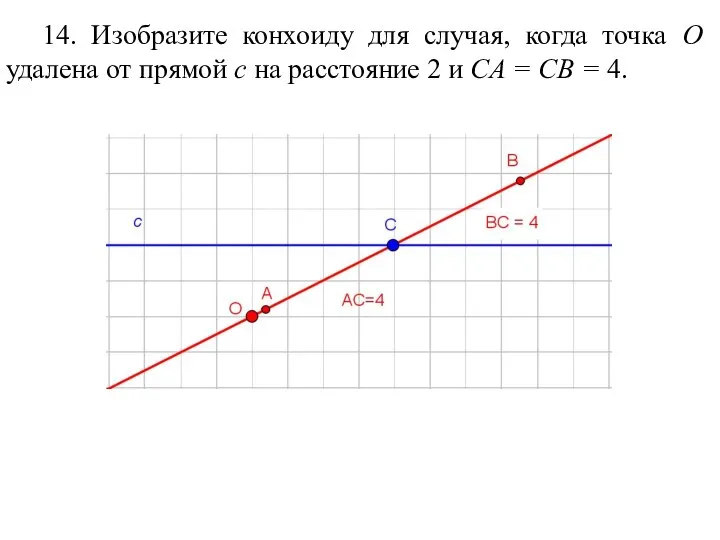
- 80. 14. Изобразите конхоиду для случая, когда точка O удалена от прямой c на расстояние 2 и
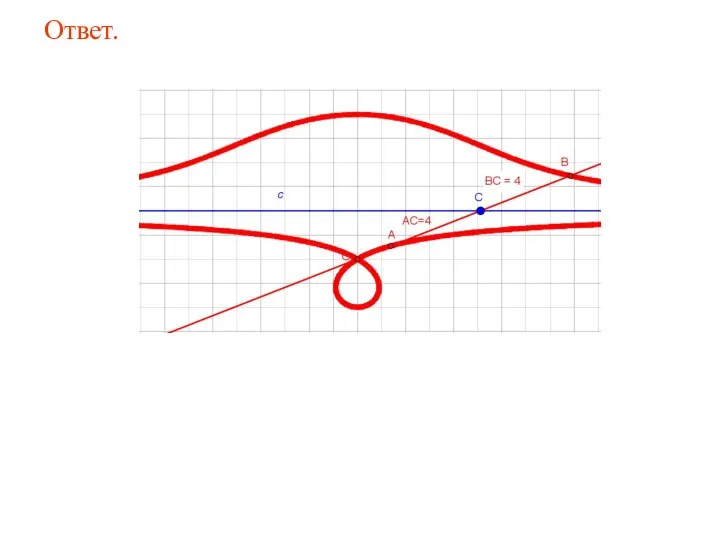
- 81. Ответ.
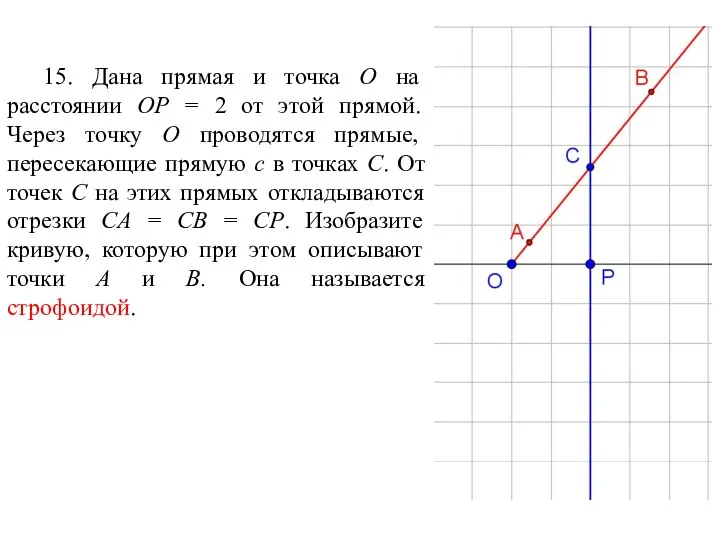
- 82. 15. Дана прямая и точка O на расстоянии OP = 2 от этой прямой. Через точку
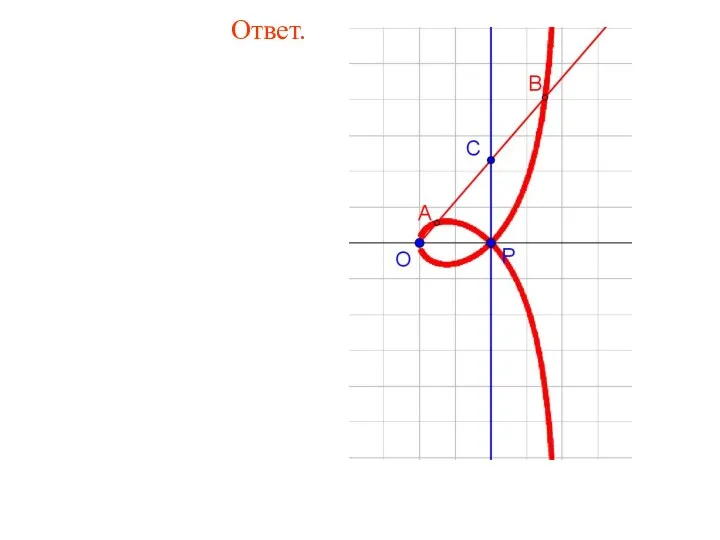
- 83. Ответ.
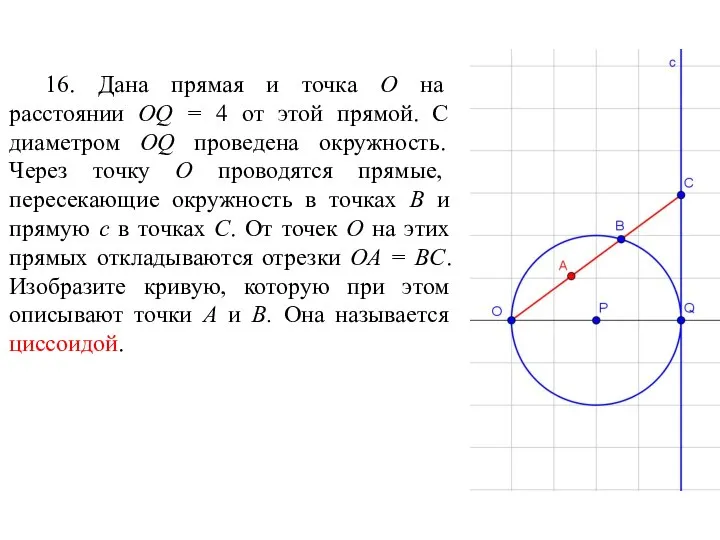
- 84. 16. Дана прямая и точка O на расстоянии OQ = 4 от этой прямой. С диаметром
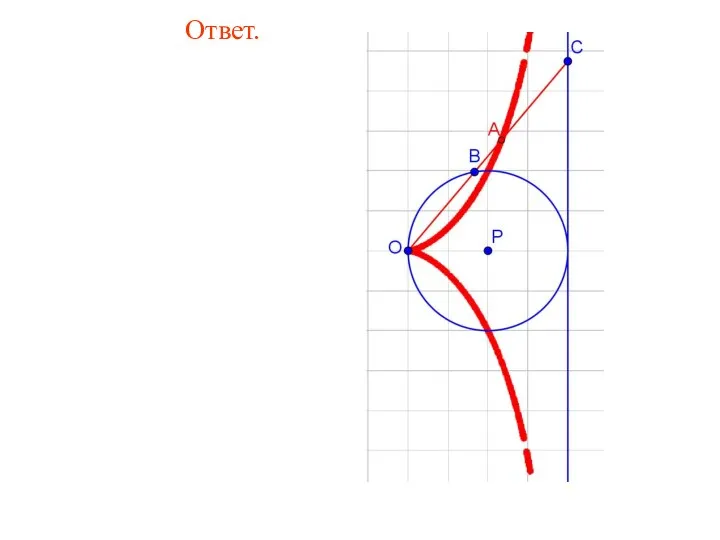
- 85. Ответ.
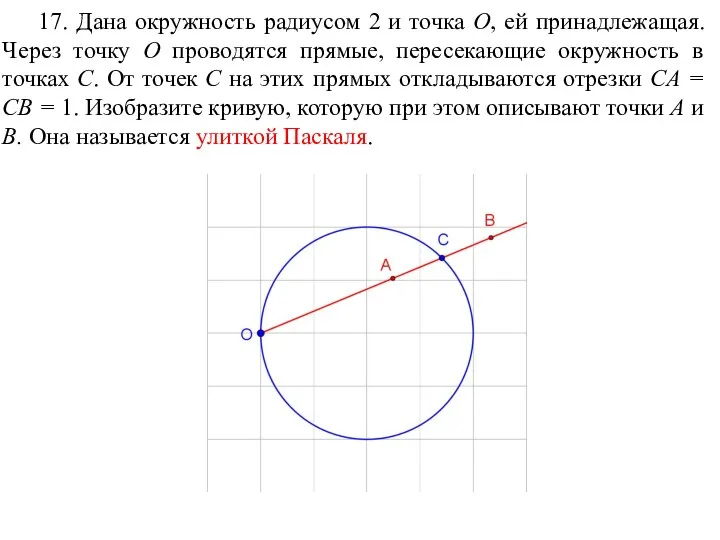
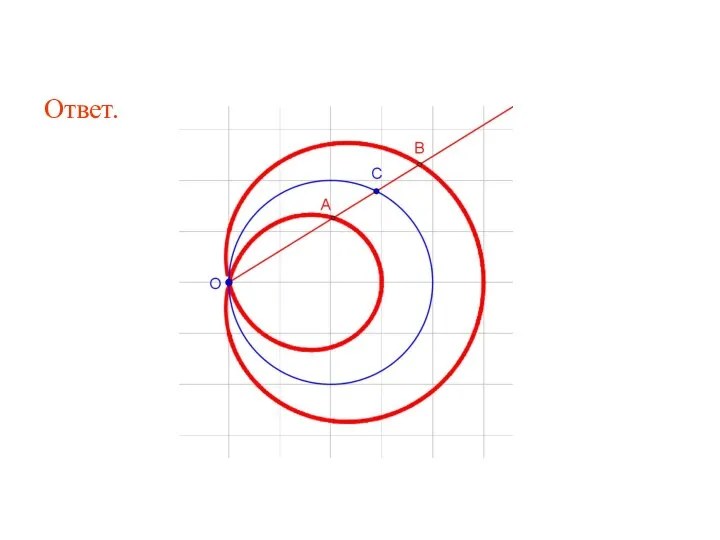
- 86. 17. Дана окружность радиусом 2 и точка O, ей принадлежащая. Через точку O проводятся прямые, пересекающие
- 87. Ответ.
- 89. Скачать презентацию








 Геометрические портреты
Геометрические портреты Логарифм
Логарифм Множества. Операции над ними
Множества. Операции над ними Компьютерное моделирование процесса подготовки РКН к пуску. Лекция 15
Компьютерное моделирование процесса подготовки РКН к пуску. Лекция 15 Квадратичная функция
Квадратичная функция Презентация на тему Решаем задачи (1 класс)
Презентация на тему Решаем задачи (1 класс)  Интегривование тригонометрических функций
Интегривование тригонометрических функций Аппроксимация функций. Метод Лагранжа
Аппроксимация функций. Метод Лагранжа Презентация на тему Теория вероятностей и комбинаторные правила
Презентация на тему Теория вероятностей и комбинаторные правила  О математическом языке
О математическом языке Формулы сокращенного умножения. Интерактивный плакат
Формулы сокращенного умножения. Интерактивный плакат Графический диктант. Тема: Делимость чисел
Графический диктант. Тема: Делимость чисел Устный счёт
Устный счёт Площади и объемы
Площади и объемы Преобразование логарифмических выражений
Преобразование логарифмических выражений Решение задач по теме Арифметическая прогрессия
Решение задач по теме Арифметическая прогрессия Моделирование при управлении рисками авиапредприятий
Моделирование при управлении рисками авиапредприятий Методика изучения массы
Методика изучения массы Единицы измерения длины. Задания
Единицы измерения длины. Задания Показатели надежности электроснабжения
Показатели надежности электроснабжения Решение задач с помощью квадратных уравнений
Решение задач с помощью квадратных уравнений Больше, меньше, столько же
Больше, меньше, столько же Свойство противоположных сторон прямоугольника
Свойство противоположных сторон прямоугольника Санкт-Петербург на уроках математики
Санкт-Петербург на уроках математики formuly_privedenia
formuly_privedenia Решение уравнений. Буквенные выражения
Решение уравнений. Буквенные выражения Неопределённый интеграл
Неопределённый интеграл Формулы дифференцирования
Формулы дифференцирования