Содержание
- 2. Самый распространённый, а иногда и единственно возможный метод решения уравнений с модулем – раскрытие модуля согласно
- 3. |x - 5| - |2x + 8| = -12 Нули подмодульных выражений: 5; -4. Значит, нужно
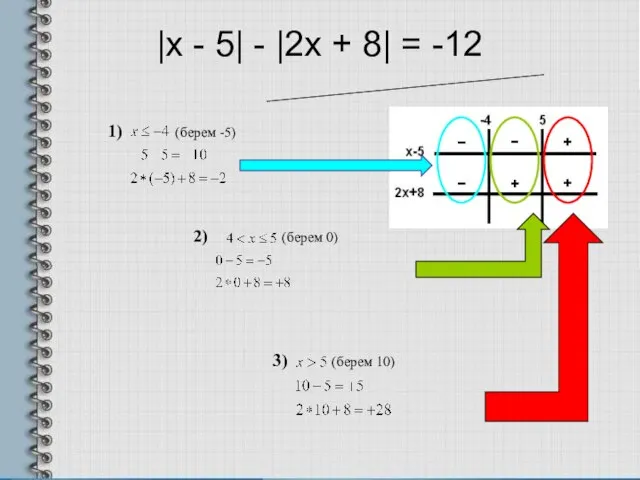
- 4. |x - 5| - |2x + 8| = -12 2) (берем 0) 1) (берем -5) 3)
- 5. На рисунке схематично показано, какой знак будут иметь подмодульные выражения на каждом из трёх промежутков: |x
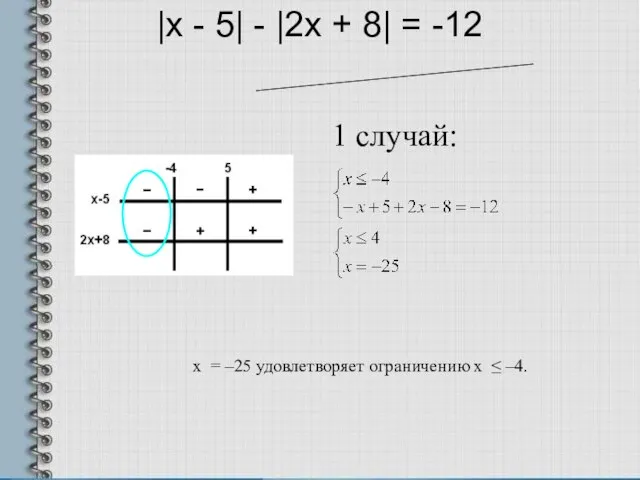
- 6. |x - 5| - |2x + 8| = -12 1 случай: x = –25 удовлетворяет ограничению
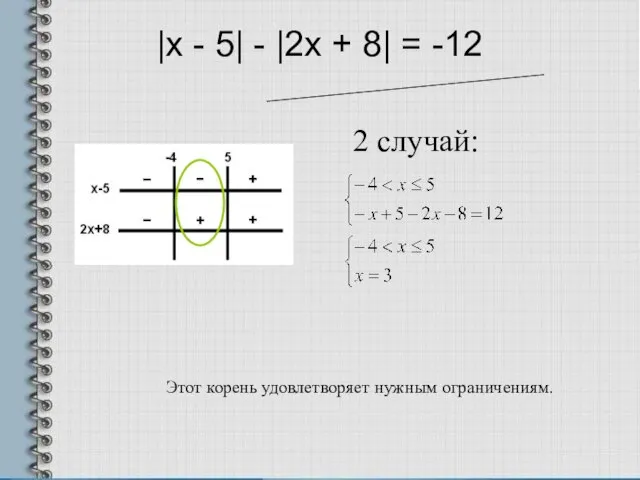
- 7. |x - 5| - |2x + 8| = -12 2 случай: Этот корень удовлетворяет нужным ограничениям.
- 9. Скачать презентацию



 Введение в стереометрию
Введение в стереометрию Следствия из аксиом I - III
Следствия из аксиом I - III Применение теоремы синусов
Применение теоремы синусов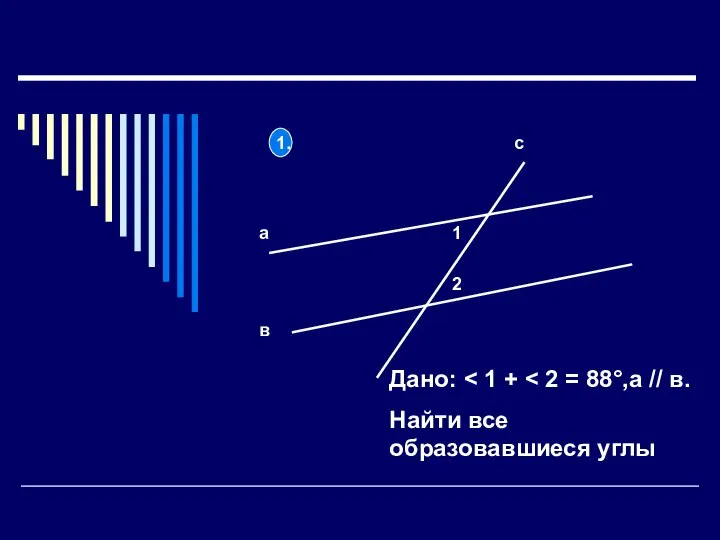 Признаки равенства треугольников
Признаки равенства треугольников Решите примеры
Решите примеры Математика и здоровье. Математика и медицина
Математика и здоровье. Математика и медицина Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Приёмы вычитания и сложения
Приёмы вычитания и сложения Примеры вычисление определенного интеграла
Примеры вычисление определенного интеграла Свойства и метода интегрирования
Свойства и метода интегрирования Табличный метод решения задач ЕГЭ по теории вероятностей
Табличный метод решения задач ЕГЭ по теории вероятностей Признаки параллельности прямых
Признаки параллельности прямых Презентация на тему Прибавление и вычитание числа 3
Презентация на тему Прибавление и вычитание числа 3  Математический тренажёр. Устные упражнения на уроках математики в 7 классе как один из способов отработки навыка устного счёта
Математический тренажёр. Устные упражнения на уроках математики в 7 классе как один из способов отработки навыка устного счёта Metode numerice
Metode numerice Деление целого на 2 части
Деление целого на 2 части СДНФ и СКНФ — два представления булевой функции
СДНФ и СКНФ — два представления булевой функции Множества и операции над множествами
Множества и операции над множествами Решение показательных уравнений
Решение показательных уравнений Учимся писать цифры
Учимся писать цифры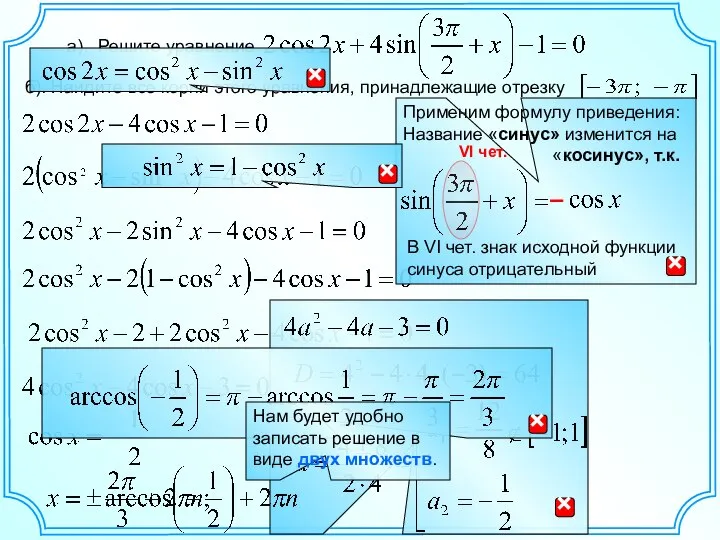 Способы отбора корней
Способы отбора корней Сфера и шар
Сфера и шар Презентация на тему Нумерация в пределах 1000
Презентация на тему Нумерация в пределах 1000  Площа криволінійної трапеції
Площа криволінійної трапеції Прикладной количественный анализ заголовков
Прикладной количественный анализ заголовков Геометрия. Билет 10
Геометрия. Билет 10 Дискретные случайные величины
Дискретные случайные величины Понятие алгоритма
Понятие алгоритма