Содержание
- 3. Предел функции в точке и на бесконечности
- 4. Замечательные пределы Первый замечательный предел Второй замечательный предел Часто используются следующие следствия:
- 5. Бесконечно малые и бесконечно большие функции.
- 6. Некоторые эквивалентные бесконечно малыми функции Данное определение особенно важно на практике, т.к. оно фактически означает, что
- 7. Раскрытие неопределенностей. К разряду неопределенностей принято относить следующие соотношения: Задача . Найти пределы . 1) 4)
- 9. Скачать презентацию






 Sam Signal Processing New2
Sam Signal Processing New2 Презентация на тему Преобразование выражений содержащих квадратные корни
Презентация на тему Преобразование выражений содержащих квадратные корни  Сумма углов треугольника. 7 класс
Сумма углов треугольника. 7 класс Перпендикулярные прямые
Перпендикулярные прямые Определение арифметического корня п-ой степени
Определение арифметического корня п-ой степени Задание из учебника Н.Б. Исиоминой. 3 класс. 2 часть
Задание из учебника Н.Б. Исиоминой. 3 класс. 2 часть Интегральное исчисление
Интегральное исчисление Распределение Максвелла
Распределение Максвелла Презентация на тему Геометрия вокруг нас
Презентация на тему Геометрия вокруг нас  Сравнение числовых выражений (Урок 30)
Сравнение числовых выражений (Урок 30) Решение задач
Решение задач Презентация на тему Показательная и логарифмическая функции
Презентация на тему Показательная и логарифмическая функции  Lektsia_po_modulnoi_774_edinitse_4_Pervoobraznaya_i_neopredelennyi_774_integral_Metody_integrirovania
Lektsia_po_modulnoi_774_edinitse_4_Pervoobraznaya_i_neopredelennyi_774_integral_Metody_integrirovania Длина окружности,
Длина окружности, Прямые на плоскости. Задачи 6 и 7
Прямые на плоскости. Задачи 6 и 7 Решение неравенств второй степени с помощью эскиза параболы
Решение неравенств второй степени с помощью эскиза параболы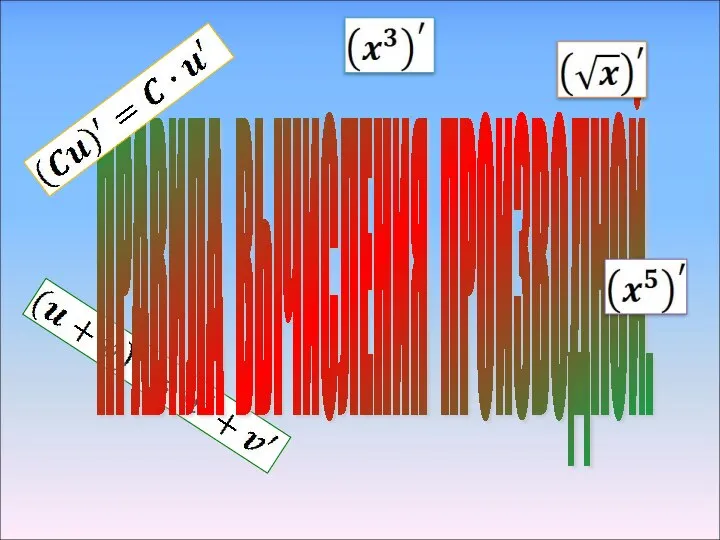 Правила вычисления производной
Правила вычисления производной Презентация на тему Действия с целыми числами
Презентация на тему Действия с целыми числами 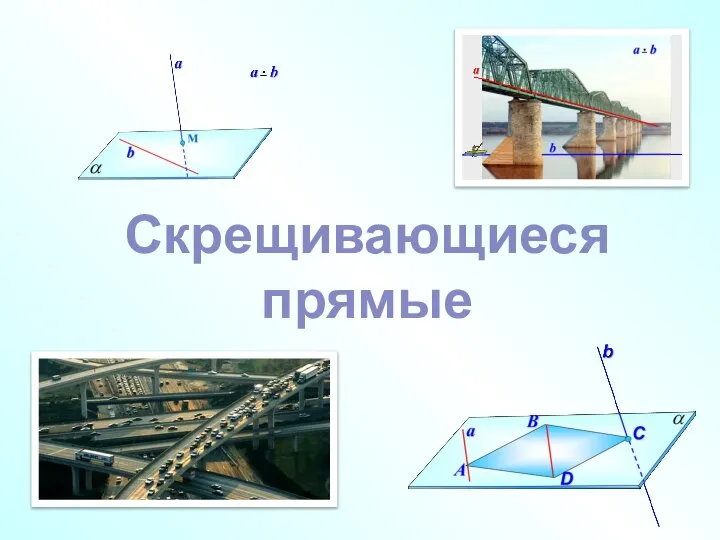 Скрещивающиеся прямые
Скрещивающиеся прямые Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами Неполные квадратные уравнения. 8 класс
Неполные квадратные уравнения. 8 класс Определение функций. Построение и чтение графиков функций
Определение функций. Построение и чтение графиков функций Построение сечений
Построение сечений Исследовательская работа. Теорема Пифагора
Исследовательская работа. Теорема Пифагора Формула Бернулли
Формула Бернулли Таблицы истинности
Таблицы истинности Взаимное расположение прямой и окружности на плоскости
Взаимное расположение прямой и окружности на плоскости Окружность. 7 класс
Окружность. 7 класс