- Главная
- Математика
- Прогрессия. Анзац

Содержание
Слайд 2РЕШИТЬ:
а1=5 а8=26 d-? (н)
b1=2 q=4 b6-? (а)
а3=5 а7=13 d-? (ц)
d=5 а10=25 а1-?
РЕШИТЬ:
а1=5 а8=26 d-? (н)
b1=2 q=4 b6-? (а)
а3=5 а7=13 d-? (ц)
d=5 а10=25 а1-?

(з)
b1=4 q=2 S5-? (а)
b1=4 q=2 S5-? (а)
Слайд 3РЕШЕНИЕ
РЕШЕНИЕ
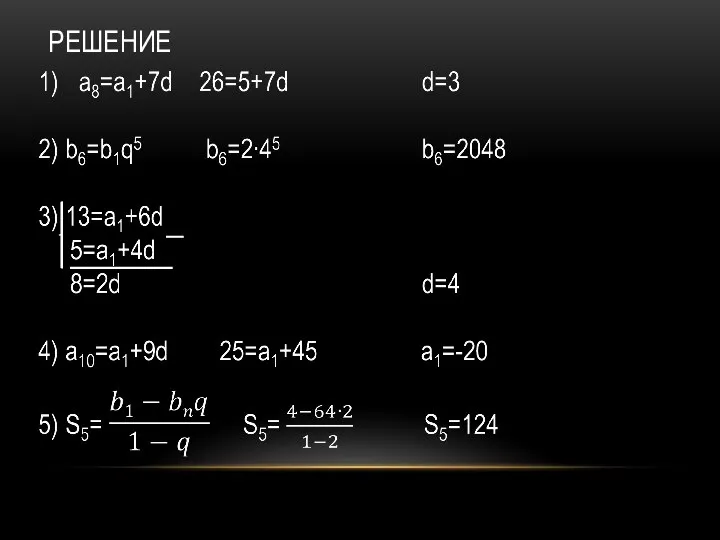
Слайд 5Aнза́ц —термин немецкого происхождения[1], обозначающий некую догадку о том, какую форму должно иметь
Aнза́ц —термин немецкого происхождения[1], обозначающий некую догадку о том, какую форму должно иметь
![Aнза́ц —термин немецкого происхождения[1], обозначающий некую догадку о том, какую форму должно](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1027897/slide-4.jpg)
решение уравнения или систем уравнений, а также само это предполагаемое решение (функцию или множество функций). Формально эта догадка может не основываться на какой-либо теории и получать подтверждение лишь после того, как найдено решение рассматриваемых уравнений.
- Предыдущая
Музыкальные шаги. Занятие №81Следующая -
Регистрация и типы аккаунтов Авито
 Шахматные головоломки. Для любителей логических задач
Шахматные головоломки. Для любителей логических задач Математическая логика
Математическая логика Скалярное прозведение векторов
Скалярное прозведение векторов Названия чисел в записях действий
Названия чисел в записях действий Гіпотеза широкого моноцентризму. Відбір за генами альтруїзму
Гіпотеза широкого моноцентризму. Відбір за генами альтруїзму Построение изображения цилиндра и его осевого сечения
Построение изображения цилиндра и его осевого сечения Усеченный конус. Часть 5
Усеченный конус. Часть 5 Римские цифры
Римские цифры Презентация на тему Перпендикуляр и наклонная
Презентация на тему Перпендикуляр и наклонная  Квадратные уравнения
Квадратные уравнения Алгоритм решения линейных уравнений
Алгоритм решения линейных уравнений Симметрия
Симметрия Работа над ошибками
Работа над ошибками Призма, её элементы
Призма, её элементы Дважды подумай. Головоломка своими руками
Дважды подумай. Головоломка своими руками Логарифмические неравенства
Логарифмические неравенства Логические задачки на умение ориентироваться в числовом ряду
Логические задачки на умение ориентироваться в числовом ряду Порог чувствительности средства измерений
Порог чувствительности средства измерений Логарифмические уравнения
Логарифмические уравнения Игра-тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление
Игра-тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление Проценты. Проценты в древности
Проценты. Проценты в древности Понятие логарифма
Понятие логарифма Статистика, вероятность, помеха, точность
Статистика, вероятность, помеха, точность Степенная функция (занятия 1, 2, 3)
Степенная функция (занятия 1, 2, 3) Проценты. Задачи
Проценты. Задачи Решение тригонометрических уравнений
Решение тригонометрических уравнений Вычисление площадей и объемов при помощи определенных интегралов. 7 Занятие
Вычисление площадей и объемов при помощи определенных интегралов. 7 Занятие Комбінаторика, як розділ математики. Сполуки без повторень. Найпростіші комбінаторні задачі
Комбінаторика, як розділ математики. Сполуки без повторень. Найпростіші комбінаторні задачі