Геометрия (8 класс)

Домашнее задание

Центральный угол
Центральный угол – угол с вершиной в центре окружности.
Градусная мера центрального угла соответствует градусной мере дуги, на которую он опирается (если дуга меньше полуокружности).
Найдите градусную меру угла АОВ.
А
В

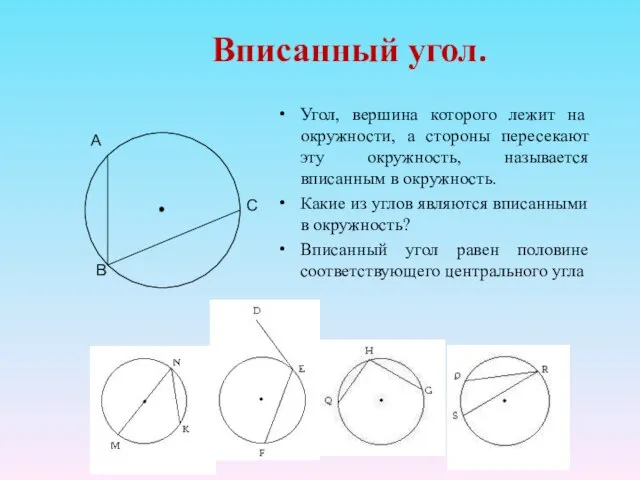
Вписанный угол.
Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным в окружность.
Какие из углов являются вписанными в окружность?
Вписанный угол равен половине соответствующего центрального угла

Описанная окружность. Треугольник, вписанный в окружность.
Окружность называется описанной около треугольника, если она проходит через все его вершины. В этом случае треугольник называется вписанным в окружность.
Стороны вписанного треугольника являются хордами описанной около него окружности.
Где лежит центр окружности, описанной около треугольника?

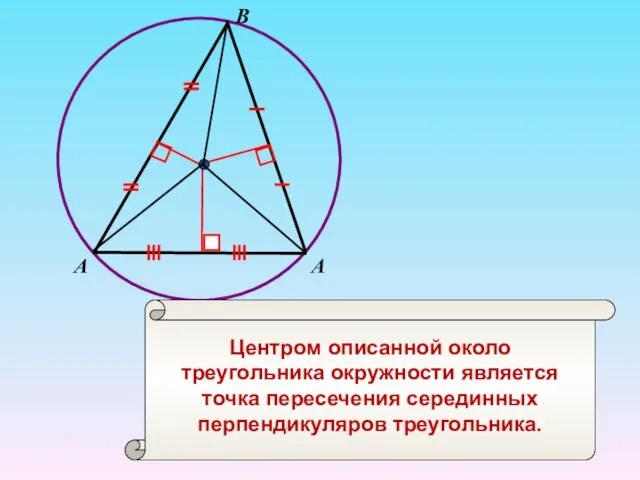
В
Центром описанной около
треугольника окружности является
точка пересечения серединных
перпендикуляров треугольника.
А
А

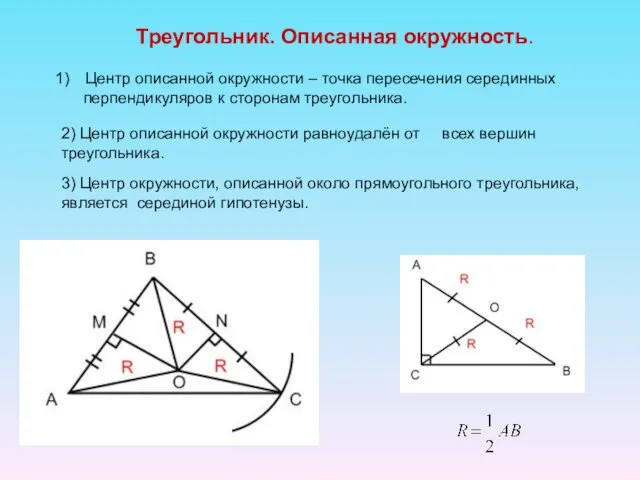
Треугольник. Описанная окружность.
Центр описанной окружности – точка пересечения серединных
перпендикуляров к сторонам треугольника.
2) Центр описанной окружности равноудалён от всех вершин треугольника.
3) Центр окружности, описанной около прямоугольного треугольника, является серединой гипотенузы.

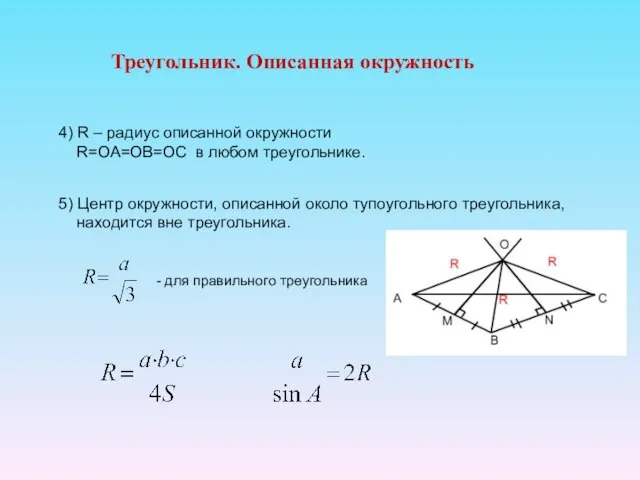
Треугольник. Описанная окружность
4) R – радиус описанной окружности
R=OA=OB=OC в любом треугольнике.
5) Центр окружности, описанной около тупоугольного треугольника,
находится вне треугольника.
- для правильного треугольника

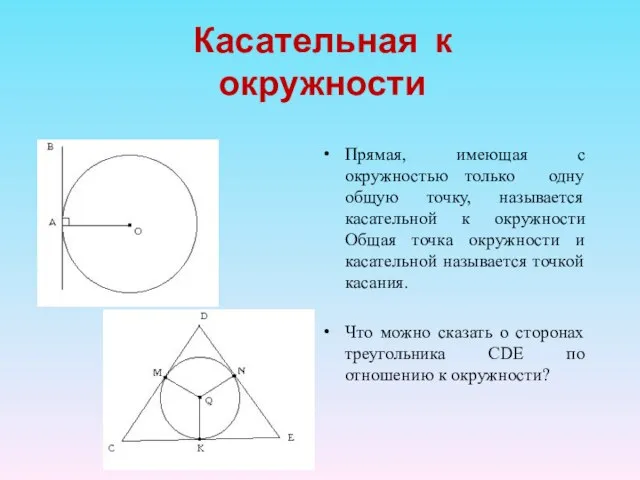
Касательная к окружности
Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности Общая точка окружности и касательной называется точкой касания.
Что можно сказать о сторонах треугольника СDЕ по отношению к окружности?

Окружность,
вписанная в треугольник.
Окружность называется вписанной в треугольник, если она касается всех его сторон. В этом случае треугольник называется описанным около окружности.
Где лежит центр окружности, вписанной в треугольник?
Треугольник ABC-описанный около окружности. Какие из треугольников AOM, MOB, BON, NOC, COK, KOA-равные?

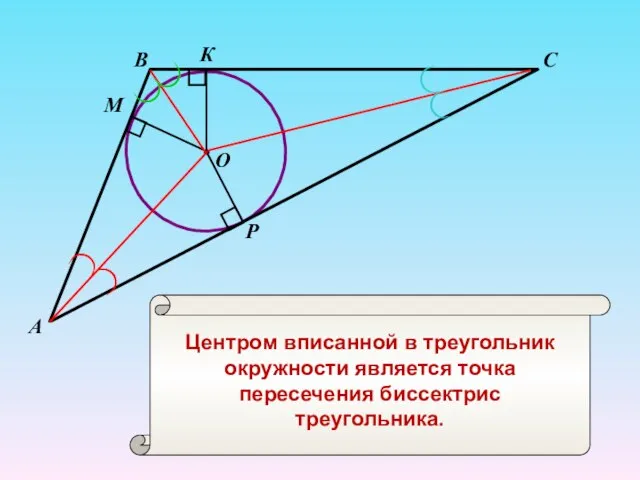
В
С
А
М
К
Р
Центром вписанной в треугольник
окружности является точка
пересечения биссектрис
треугольника.
О

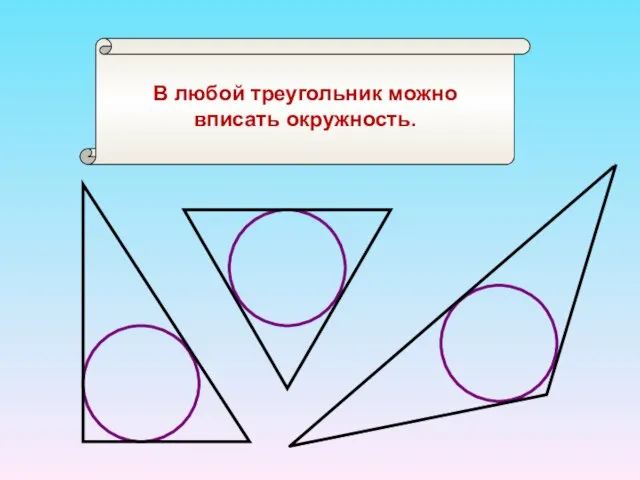
В любой треугольник можно
вписать окружность.

Треугольник. Вписанная окружность.
1) Центр вписанной окружности в треугольник – точка пересечения биссектрис.
2) Центр вписанной окружности равноудалён от сторон треугольника.
3)
p – полупериметр треугольника, r – радиус вписанной окружности
p - полупериметр
В правильном треугольнике
C – гипотенуза

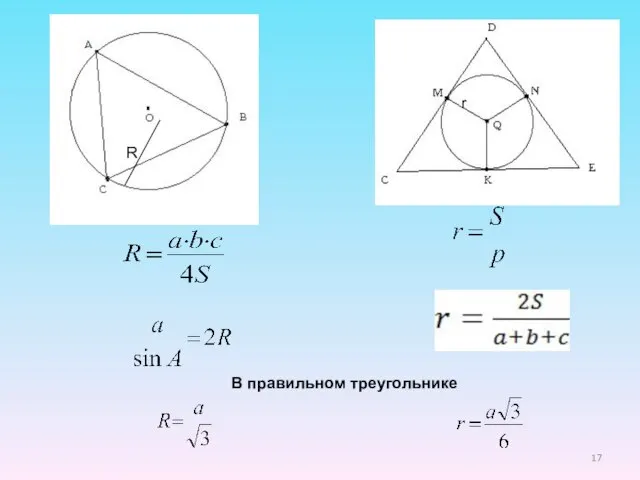
В правильном треугольнике
R
r

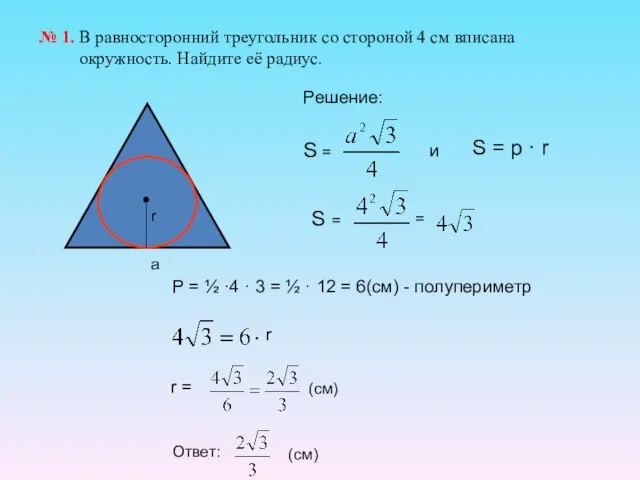
№ 1. В равносторонний треугольник со стороной 4 см вписана
окружность. Найдите её радиус.
P = ½ ·4 · 3 = ½ · 12 = 6(см) - полупериметр
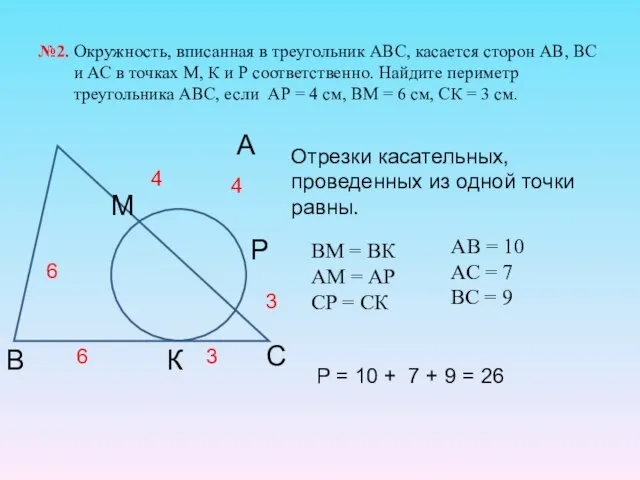
Решение:

№2. Окружность, вписанная в треугольник АВС, касается сторон АВ, ВС и АС в точках М, К и Р соответственно. Найдите периметр треугольника АВС, если АР = 4 см, ВМ = 6 см, СК = 3 см.
А
В
С
М
К
Р
4
3
6
Отрезки касательных, проведенных из одной точки равны.
ВМ = ВК
АМ = АР
СР = СК
6
3
4
АВ = 10
АС = 7
ВС = 9
Р = 10 + 7 + 9 = 26

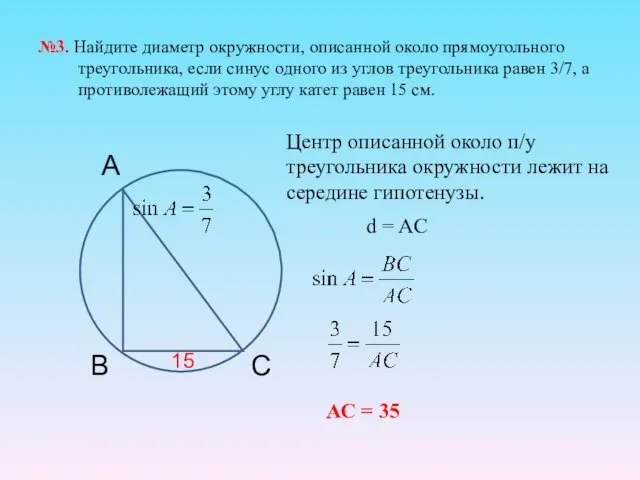
№3. Найдите диаметр окружности, описанной около прямоугольного треугольника, если синус одного из углов треугольника равен 3/7, а противолежащий этому углу катет равен 15 см.
А
В
С
Центр описанной около п/у треугольника окружности лежит на середине гипотенузы.
d = AC
15
АС = 35

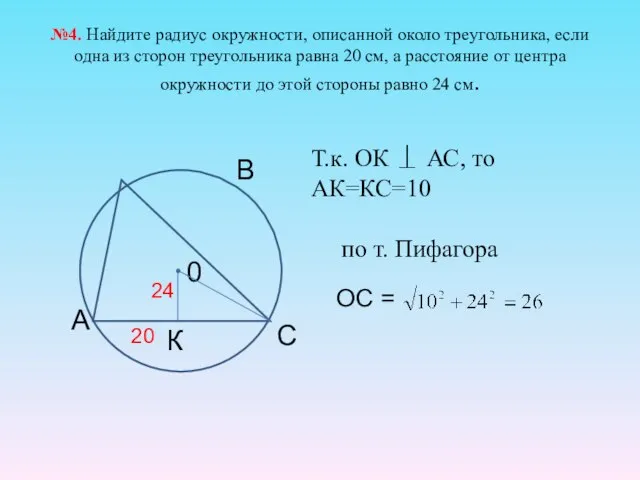
№4. Найдите радиус окружности, описанной около треугольника, если одна из сторон треугольника равна 20 см, а расстояние от центра окружности до этой стороны равно 24 см.
0
А
В
20
С
24
Т.к. ОК АС, то АК=КС=10
К
по т. Пифагора
ОС =

Домашнее задание

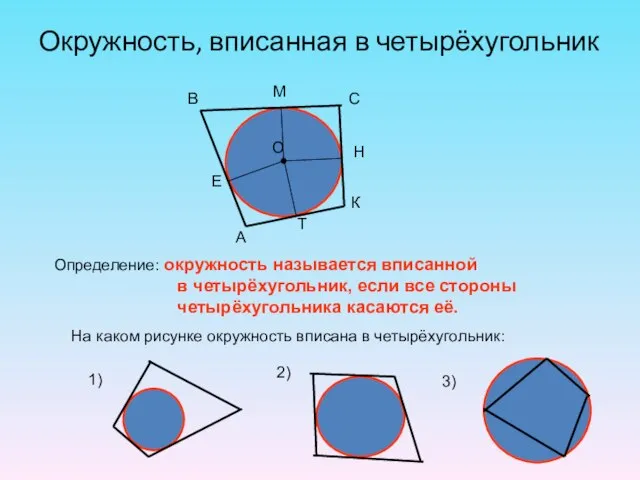
Окружность, вписанная в четырёхугольник
Определение: окружность называется вписанной
в четырёхугольник, если все стороны четырёхугольника касаются её.

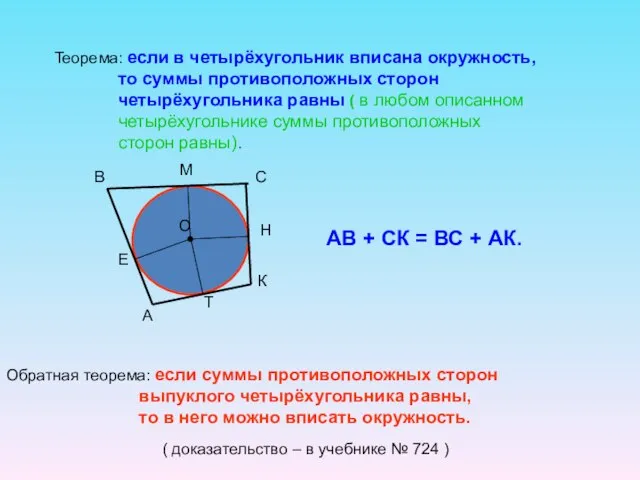
Теорема: если в четырёхугольник вписана окружность,
то суммы противоположных сторон
четырёхугольника равны ( в любом описанном
четырёхугольнике суммы противоположных
сторон равны).
Обратная теорема: если суммы противоположных сторон
выпуклого четырёхугольника равны,
то в него можно вписать окружность.
АВ + СК = ВС + АК.
( доказательство – в учебнике № 724 )

Задача: в ромб, острый угол которого 600, вписана окружность,
радиус которой равен 2 см. Найти периметр ромба.
Решение:

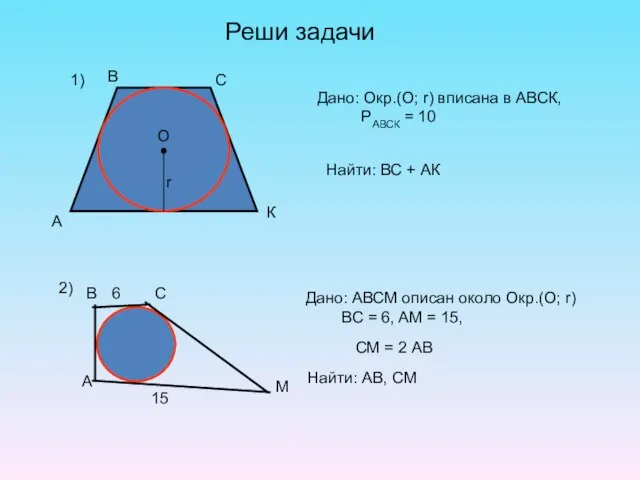
Реши задачи