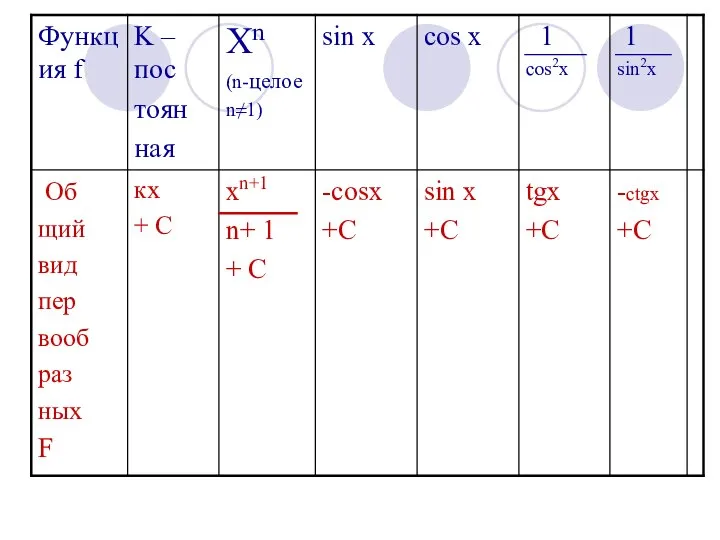
Слайд 2Вопросы для повторения
1.Что называют криволинейной трапецией?
2. Являются ли фигуры, изображённые на графиках

криволинейными трапециями?
3. Запишите формулу для вычисления площади криволинейной трапеции
.
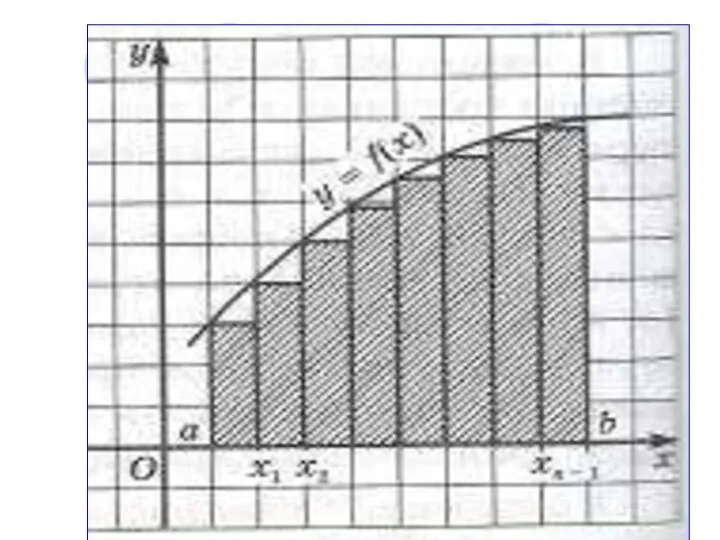
Слайд 3Рассмотрим другой подход к вычислению площади криволинейной трапеции
Будем считать функцию f неотрицательной

и непрерывной на отрезке [а; в], тогда площадь S соответствующей криволинейной трапеции можно приближённо подсчитать следующим образом
Слайд 5Разобьём отрезок [а; в] на n отрезков одинаковой длины точками
![Разобьём отрезок [а; в] на n отрезков одинаковой длины точками](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/974273/slide-4.jpg)
Слайд 6При n → ∞
Sn→ к некоторому числу. Это число называют интегралом

функции f от а до в и обозначают:
в
∫ f(х)dх
а
Слайд 7 Числа а и в - называются пределами
интегрирования, а –

нижним пределом, в – верхним.
Знак ∫ - называют знаком интеграла
Функцию f называют подынтегральной функцией, а переменная х – переменной интегрирования
df- знак дифференциала
Слайд 8 Итак, если f( х ) ≥0 на отрезке [а; в], то
![Итак, если f( х ) ≥0 на отрезке [а; в], то Площадь](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/974273/slide-7.jpg)
Площадь соответствующей криволинейной трапеции выражается формулой:
в
S = ∫ f(х)dх
а
Слайд 9Сравнивая формулы криволинейных трапеций :
в
S = ∫ f(х)dх и S

= F(в) – F(а)
а
Делаем вывод:


![Разобьём отрезок [а; в] на n отрезков одинаковой длины точками](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/974273/slide-4.jpg)


![Итак, если f( х ) ≥0 на отрезке [а; в], то Площадь](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/974273/slide-7.jpg)




 Презентация на тему Числовые и алгебраические выражения
Презентация на тему Числовые и алгебраические выражения  История счета и систем счисления
История счета и систем счисления Угол между прямой и плоскостью. Угол между плоскостями
Угол между прямой и плоскостью. Угол между плоскостями Умножение десятичных дробей
Умножение десятичных дробей Синус и косинус
Синус и косинус Своя игра. Тесная связь математики с другими науками
Своя игра. Тесная связь математики с другими науками Центральные и вписанные углы
Центральные и вписанные углы Логарифмические уравнения
Логарифмические уравнения Треугольник
Треугольник Свойства степени
Свойства степени Перпендикуляр и наклонная
Перпендикуляр и наклонная Тела вращения
Тела вращения Логарифмические неравенства
Логарифмические неравенства КВН Знакомьтесь: геометрия
КВН Знакомьтесь: геометрия Результаты пробных ЕГЭ по математике (2013-2014 учебный год)
Результаты пробных ЕГЭ по математике (2013-2014 учебный год) Признаки делимости
Признаки делимости Применение теории графов
Применение теории графов Задача по математике (1 класс, задание 15)
Задача по математике (1 класс, задание 15) Числа и точки на прямой. 5 класс
Числа и точки на прямой. 5 класс Формулы двойного аргумента
Формулы двойного аргумента Закон пропорциональности
Закон пропорциональности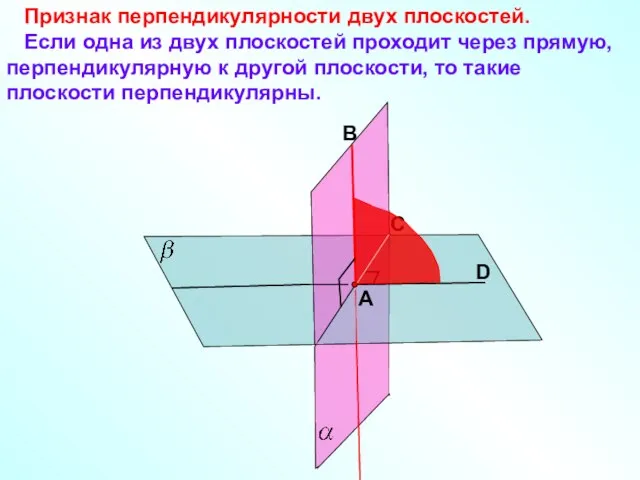 Признак перпендикулярности двух плоскостей
Признак перпендикулярности двух плоскостей Знак деления
Знак деления Теорема Пифагора
Теорема Пифагора Умножение и деление натуральных чисел. Устный счет
Умножение и деление натуральных чисел. Устный счет Периметр прямоугольника. Площадь прямоугольника. Путь. (5 класс)
Периметр прямоугольника. Площадь прямоугольника. Путь. (5 класс) Правильные многогранники в природе
Правильные многогранники в природе Стереометрические задачи повышенной сложности
Стереометрические задачи повышенной сложности