Содержание
- 2. План Классификация: общие принципы Кластеризация методом К средних Классификация методом SIMCA
- 3. Можно ли по спектру отличить кетон от эфира? Можно ли определить пол человека по его ответам
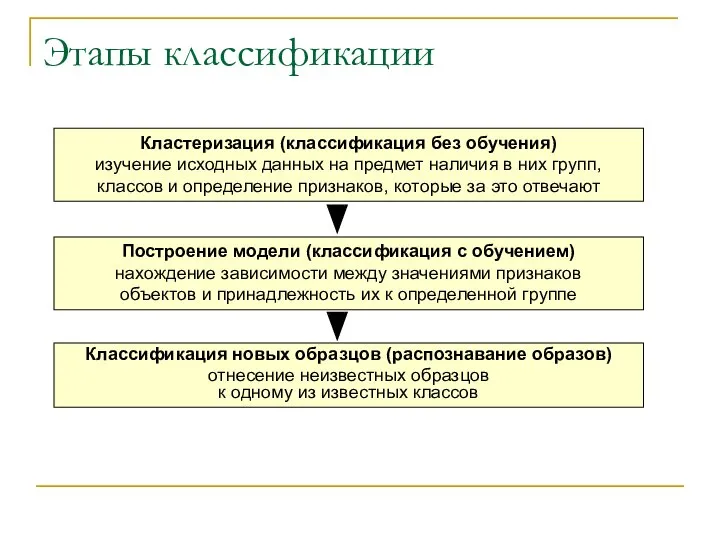
- 4. Этапы классификации Кластеризация (классификация без обучения) изучение исходных данных на предмет наличия в них групп, классов
- 5. Алгоритмы классификации Без обучения (Unsupervised) C обучением (Supervised) Априори не известно существуют ли скрытые группы в
- 6. С чем работаем? Объект — все, что угодно: пациент, вещество, предмет, пиксел, изображение и т.д. Вектор
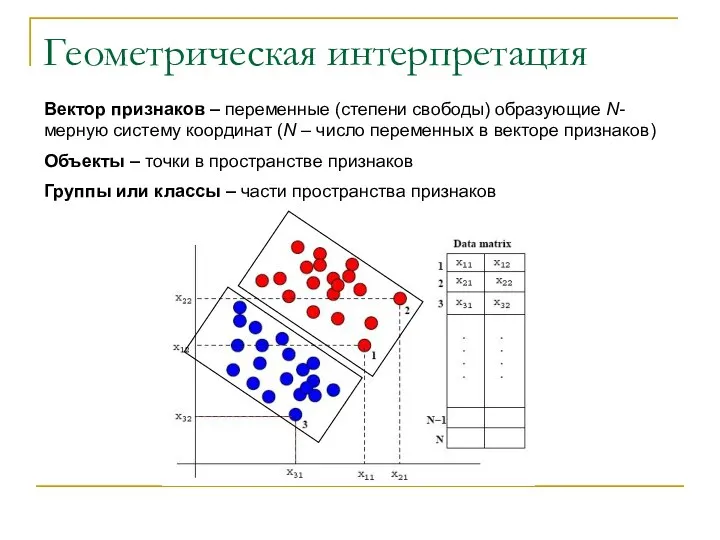
- 7. Геометрическая интерпретация Вектор признаков – переменные (степени свободы) образующие N-мерную систему координат (N – число переменных
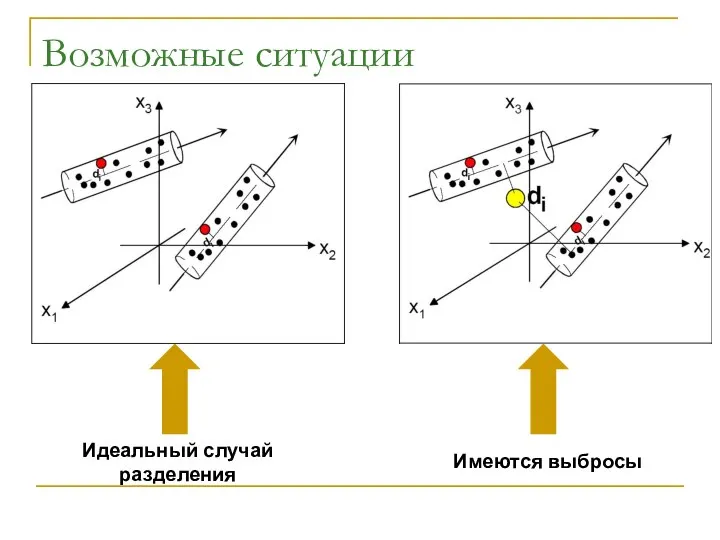
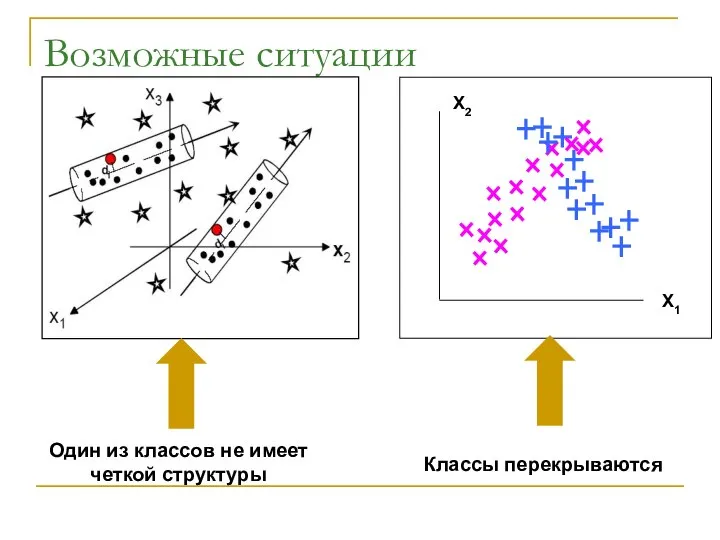
- 8. Возможные ситуации
- 9. Возможные ситуации
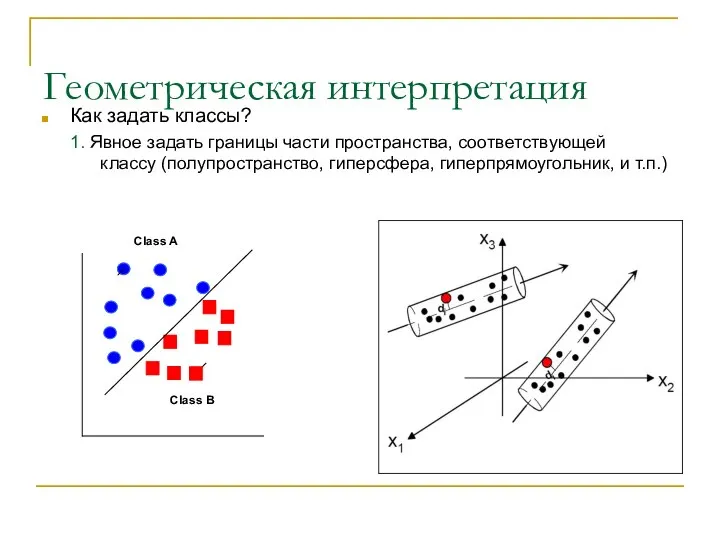
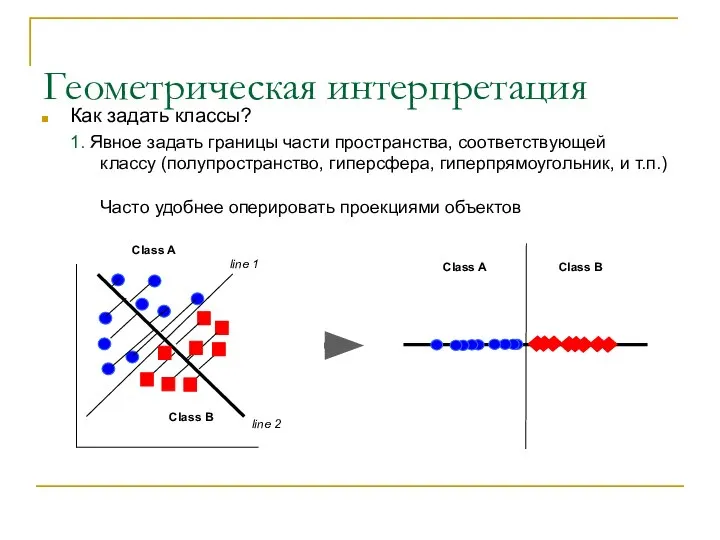
- 10. Геометрическая интерпретация Как задать классы? 1. Явное задать границы части пространства, соответствующей классу (полупространство, гиперсфера, гиперпрямоугольник,
- 11. Геометрическая интерпретация Как задать классы? 1. Явное задать границы части пространства, соответствующей классу (полупространство, гиперсфера, гиперпрямоугольник,
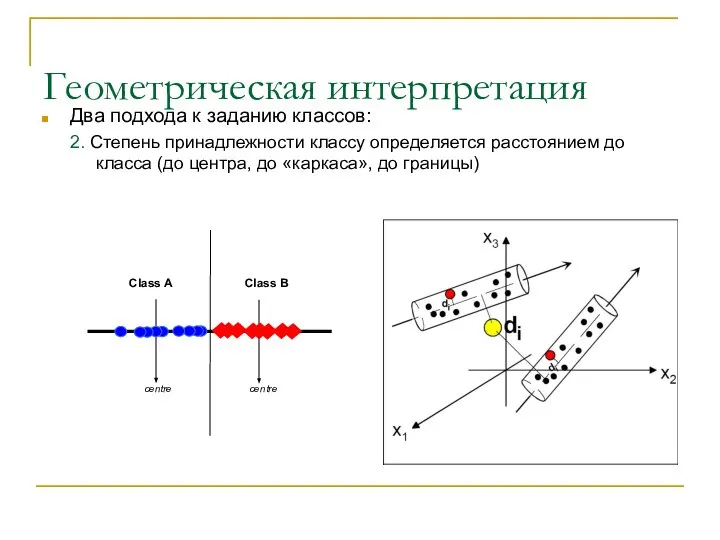
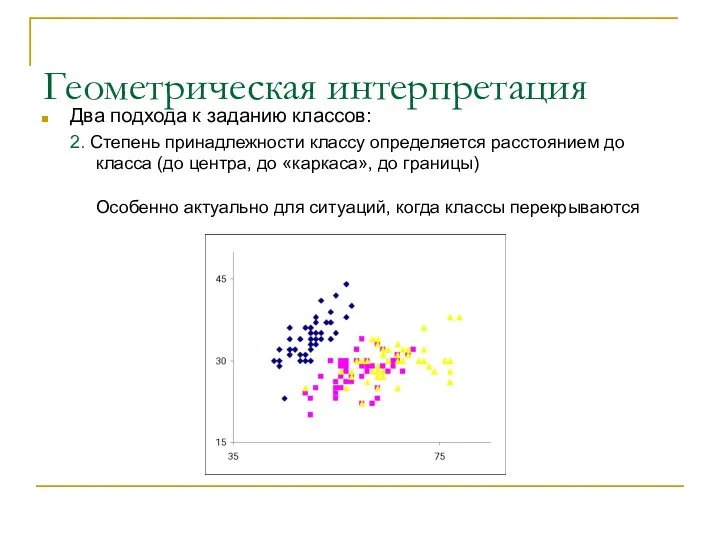
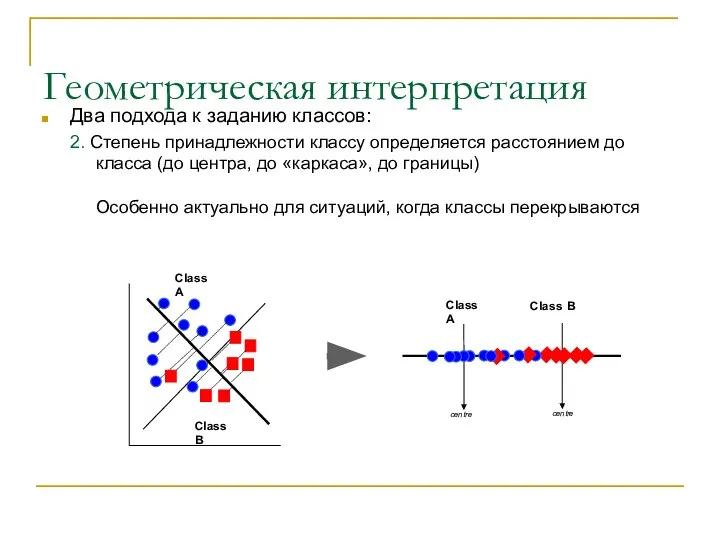
- 12. Геометрическая интерпретация Два подхода к заданию классов: 2. Степень принадлежности классу определяется расстоянием до класса (до
- 13. Геометрическая интерпретация Два подхода к заданию классов: 2. Степень принадлежности классу определяется расстоянием до класса (до
- 14. Геометрическая интерпретация Два подхода к заданию классов: 2. Степень принадлежности классу определяется расстоянием до класса (до
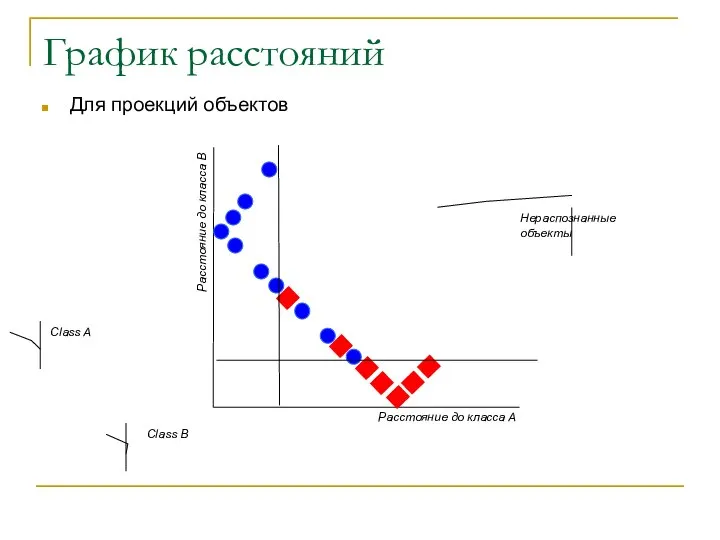
- 15. График расстояний Для проекций объектов Class B Class A Нераспознанные объекты Расcтояние до класса A Расcтояние
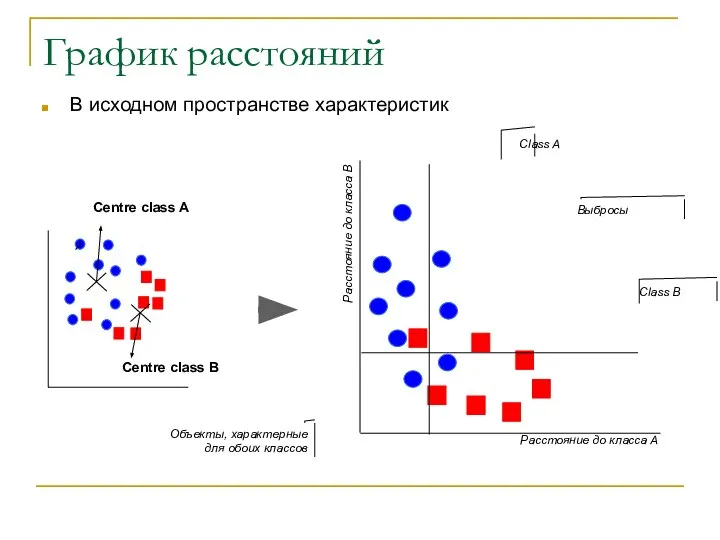
- 16. График расстояний В исходном пространстве характеристик Centre class A Centre class B Class A Class B
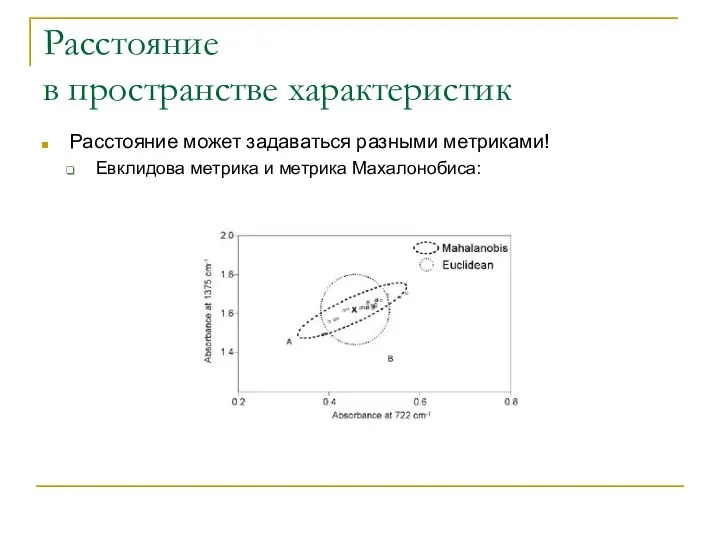
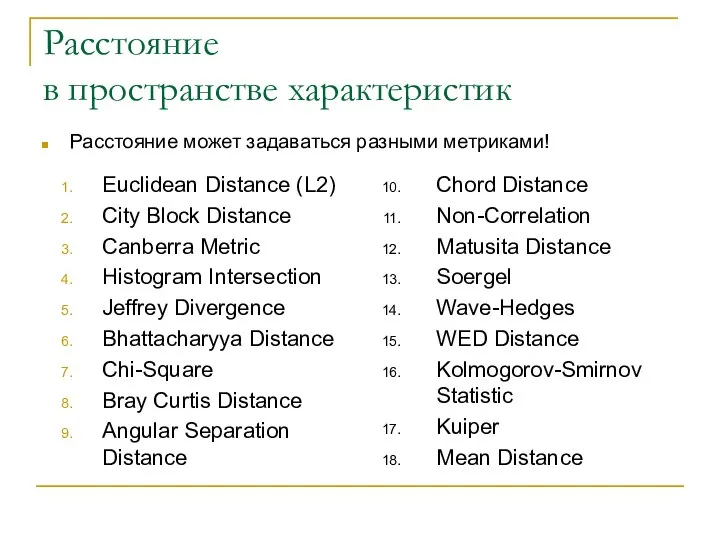
- 17. Расстояние в пространстве характеристик Расстояние может задаваться разными метриками! Евклидова метрика: Метрика Махалонобиса: Каждая переменная вектора
- 18. Расстояние в пространстве характеристик Расстояние может задаваться разными метриками! Евклидова метрика и метрика Махалонобиса:
- 19. Расстояние в пространстве характеристик Расстояние может задаваться разными метриками! Euclidean Distance (L2) City Block Distance Canberra
- 20. Виды ошибок Измерения ошибки как «вероятности выдать неверный ответ» может быть не всегда достаточно 15% ошибки
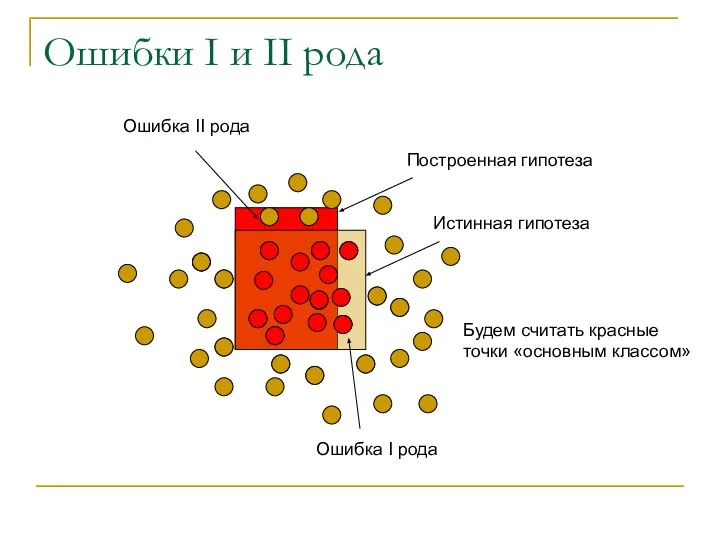
- 21. Ошибки I и II рода Пусть, существует «основной класс» Обычно, это класс, при обнаружении которого, предпринимается
- 22. Ошибки I и II рода Истинная гипотеза Ошибка II рода Ошибка I рода Построенная гипотеза Будем
- 23. Ошибки I и II рода Что считать основным классом зависит полностью от прикладной специфики Особенно важно
- 24. Чувствительность vs Избирательность Чувствительность – вероятность дать правильный ответ на пример основного класса Избирательность – вероятность
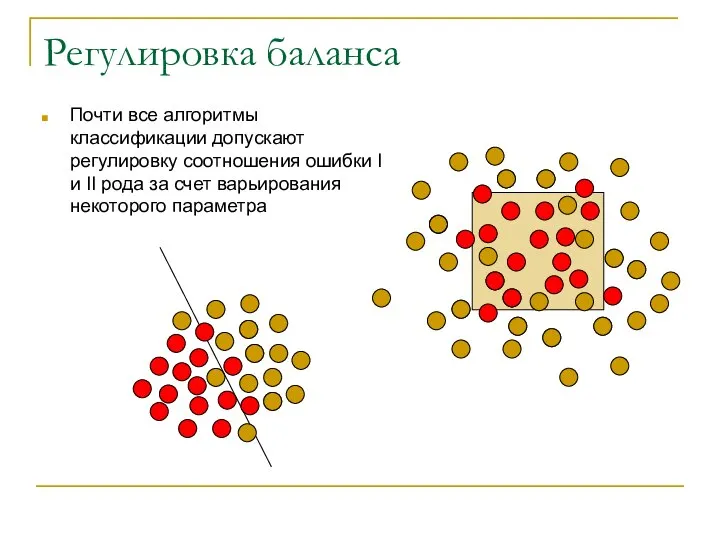
- 25. Регулировка баланса Почти все алгоритмы классификации допускают регулировку соотношения ошибки I и II рода за счет
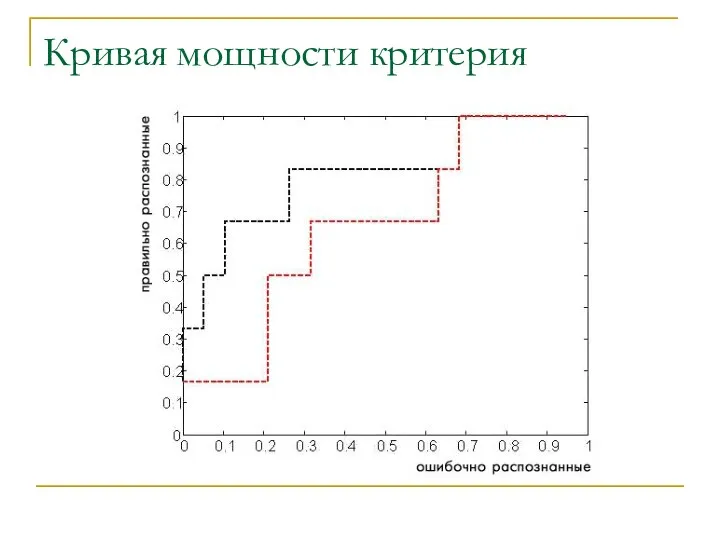
- 26. Кривая мощности критерия
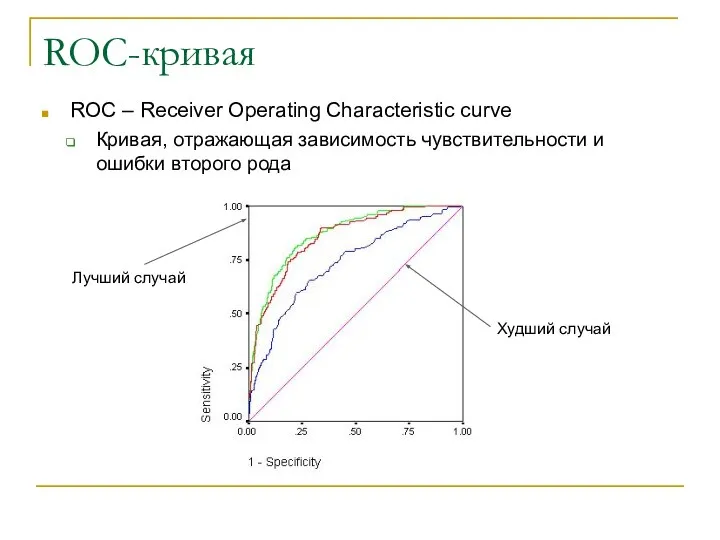
- 27. ROC-кривая ROC – Receiver Operating Characteristic curve Кривая, отражающая зависимость чувствительности и ошибки второго рода Худший
- 28. Построение ROC-кривой Для различных значений параметра строится таблица ошибок Сам параметр в таблице не участвует! Классификатор
- 29. Анализ ROC кривой Площадь под графиком – AUC Дает некоторый объективный показатель качества классификатора Позволяет сравнивать
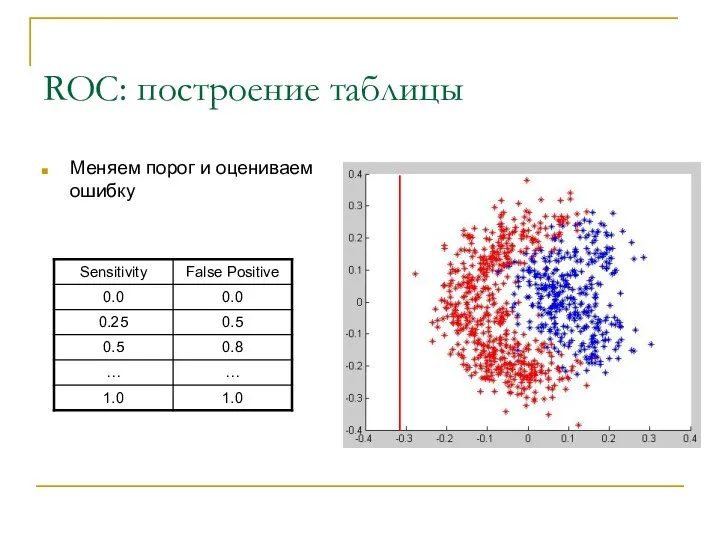
- 30. ROC: построение таблицы Меняем порог и оцениваем ошибку
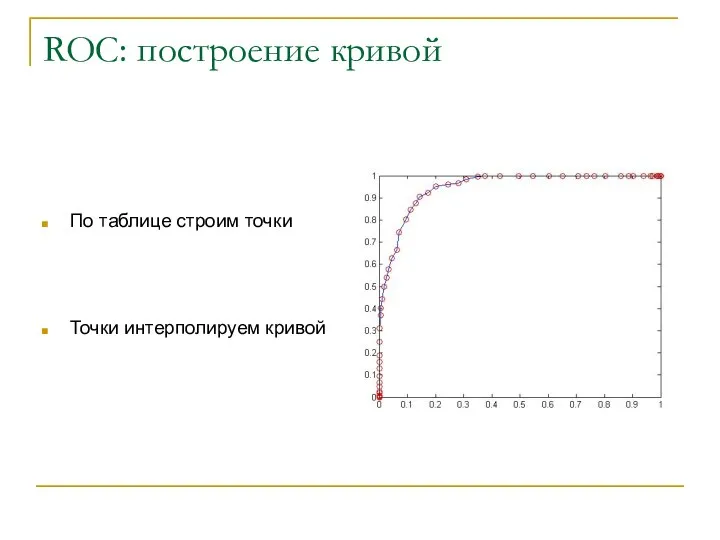
- 31. ROC: построение кривой По таблице строим точки Точки интерполируем кривой
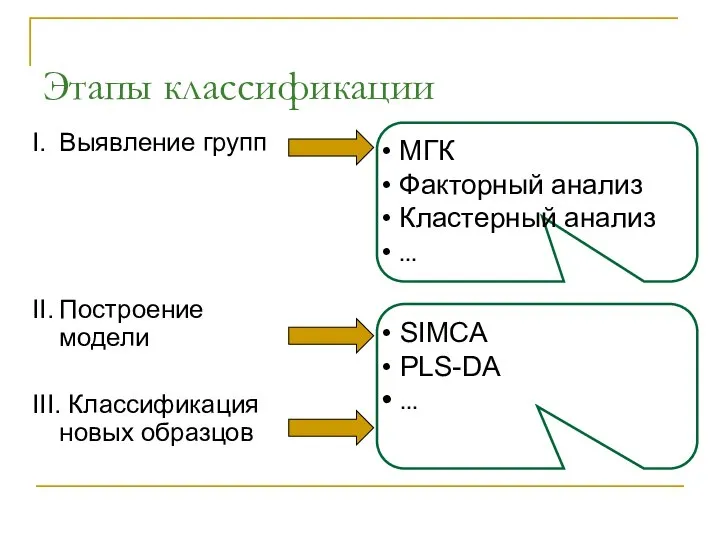
- 32. Этапы классификации I. Выявление групп II. Построение модели III. Классификация новых образцов МГК Факторный анализ Кластерный
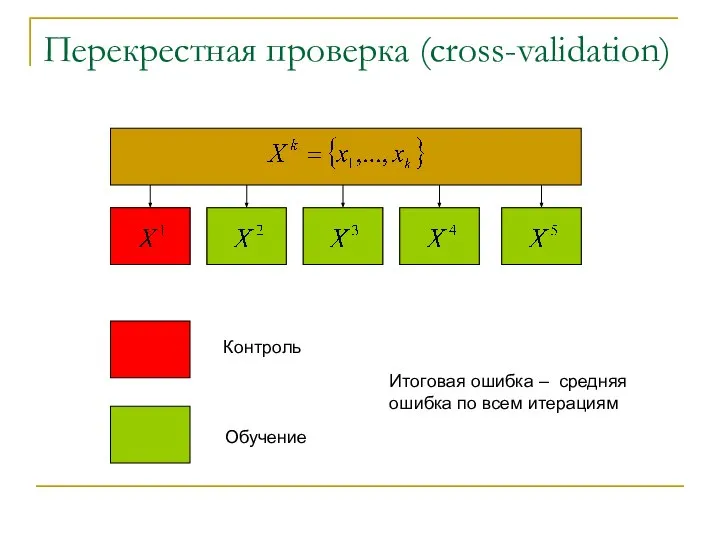
- 33. Перекрестная проверка (cross-validation) Итоговая ошибка – средняя ошибка по всем итерациям
- 35. Скачать презентацию











 Решение квадратных уравнений
Решение квадратных уравнений Длина окружности
Длина окружности Лічба в межах 20. Складання і розв’язування задач на знаходження суми й остачі. Побудова відрізків заданої довжини
Лічба в межах 20. Складання і розв’язування задач на знаходження суми й остачі. Побудова відрізків заданої довжини Геометрическое решение задачи о расстояниях между точками
Геометрическое решение задачи о расстояниях между точками Индивидуальный проект на тему Золотое сечение в природе
Индивидуальный проект на тему Золотое сечение в природе Признаки равенства треугольников
Признаки равенства треугольников Решение задач с помощью уравнений. 7 класс
Решение задач с помощью уравнений. 7 класс Теорія множин. Відношення
Теорія множин. Відношення Числовые выражения
Числовые выражения Презентация на тему Сечения
Презентация на тему Сечения  Презентация на тему ЛОГАРИФМЫ И ИХ СВОЙСТВА
Презентация на тему ЛОГАРИФМЫ И ИХ СВОЙСТВА  Теорема о рациональном корне многочлена с целыми коэффициентами
Теорема о рациональном корне многочлена с целыми коэффициентами Комбинаторика
Комбинаторика Вероятность и статистика
Вероятность и статистика Математические игры
Математические игры Презентация на тему Призма: виды и особенности
Презентация на тему Призма: виды и особенности  Знакомимся с многоугольниками
Знакомимся с многоугольниками Aproximarea numerică a funcţiilor. Metode numerice – curs 11
Aproximarea numerică a funcţiilor. Metode numerice – curs 11 Тренажёр Теремок. Математика - 1 класс
Тренажёр Теремок. Математика - 1 класс P-ичная арифметика. Решение задач
P-ичная арифметика. Решение задач Сложение и вычитание в пределах 20
Сложение и вычитание в пределах 20 Площадь треугольника
Площадь треугольника Перпендикулярные прямые
Перпендикулярные прямые Арифметический корень степени п
Арифметический корень степени п Нумерация. Подготовка к ВПР
Нумерация. Подготовка к ВПР Динамика нелинейного тентообразного отображения с параметром
Динамика нелинейного тентообразного отображения с параметром Скрипт параллелограм
Скрипт параллелограм Занятие 1. Вводное занятие
Занятие 1. Вводное занятие