Слайд 2Повторение :
Сформулируйте определение производной функции в точке.
Сформулируйте правила вычисления производных.
Какая функция называется

сложной.
Сформулируйте правило нахождения производной сложной функции.
Слайд 41. Понятие дифференциала функции.
Определение: Дифференциалом функции у=f(х) в точке
называется главная

часть приращения функции.
Слайд 6Вычислите дифференциалы функций:

Слайд 72.Понятие первообразной и неопределенного интеграла

Слайд 9Если функция F(x) является первообразной для функции f(x), где хє(а;в),то множество всех

первообразных для функции f(х) задается формулой F(x)+C,где
С-произвольная постоянная величина.
Слайд 10Определение 2:
Совокупность всех первообразных F(x)+C функции f(x),xє(а,в) называется неопределенным интегралом от функции

f(x).
Записывается ∫f(x)dx=F(x)+C
Слайд 11∫-знак интеграла;
f(x)-подинтегральная функция;
f(x)dx-подинтегральное выражение;
х-переменная интегрирования;
С- постоянная интегрирования.

Слайд 13Пример с проверкой (формула 1) :

Слайд 14Замечания:
Нахождение функции по ее производной называется интегрированием(от integratio-восстановление);
Интегрирование- действие обратное дифференцированию;
Правильность интегрирования

проверяется нахождением производной.
Слайд 153.Геометрический смысл неопределенного интеграла
Неопределенный интеграл представляет собой семейство интегральных кривых, каждая из
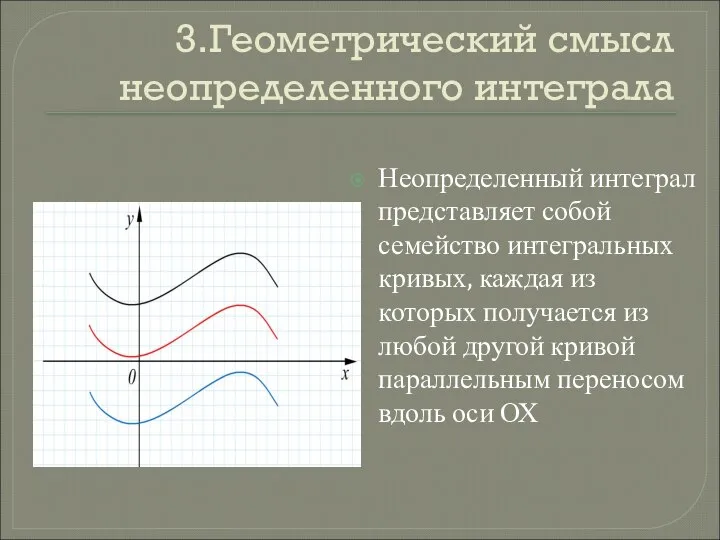
которых получается из любой другой кривой параллельным переносом вдоль оси ОХ
Слайд 164.Основные свойства неопределенного интеграла
Производная от неопределенного интеграла равна подинтегральной функции:(∫f(x)dx)'=f(x);
Дифференциал от неопределенного

интеграла равен подинтегральному выражению:d∫f(x)dx=f(x)dx;
Слайд 173. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная

постоянная:
∫dF(x)=F(x)+C;
4. Постоянный множитель можно выносить за знак интеграла:
∫af(x)dx=a∫f(x)dx;
5. Интеграл от суммы непрерывных функций равен сумме интегралов слагаемых:
∫(f(x)+g(x))dx=∫f(x)dx+g(x)dx.
Слайд 27Задания на уроке Найдите интегралы следующих функци (без 7 примера):




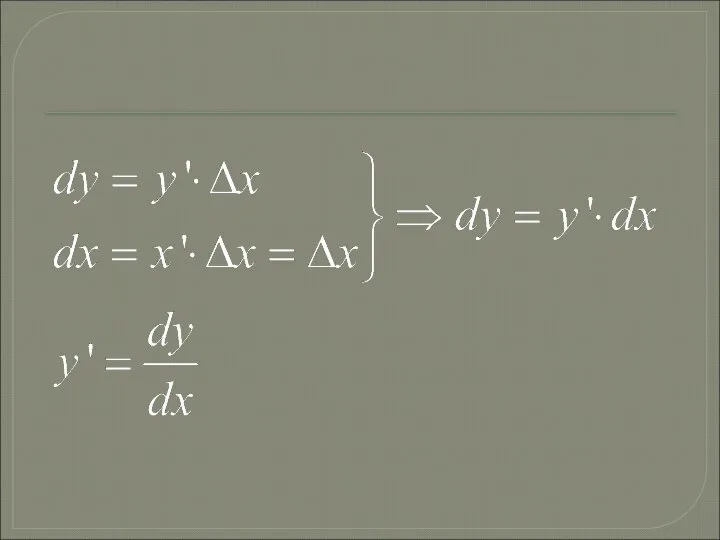






















 Соотношения между сторонами и углами прямоугольного треугольника
Соотношения между сторонами и углами прямоугольного треугольника Презентация на тему Параллельность прямых и плоскостей (10 класс)
Презентация на тему Параллельность прямых и плоскостей (10 класс)  Равносильность формул
Равносильность формул Методы решения систем линейных уравнений: метод сложения
Методы решения систем линейных уравнений: метод сложения Применение распределительного свойства умножения
Применение распределительного свойства умножения Плоскости
Плоскости Параллельные и перпендикулярные прямые
Параллельные и перпендикулярные прямые Устный счёт. Транспорт
Устный счёт. Транспорт Неопределенный интеграл. Способы вычисления
Неопределенный интеграл. Способы вычисления Презентация на тему Деление многозначных чисел
Презентация на тему Деление многозначных чисел  Понятие процента
Понятие процента Умножение пяти, на 5 и соответствующие случаи деления. Математика 3 класс. Учителя начальных классов Лаишевской специальной школ
Умножение пяти, на 5 и соответствующие случаи деления. Математика 3 класс. Учителя начальных классов Лаишевской специальной школ Математика в профессии сварщика
Математика в профессии сварщика Производные некоторых элементарных функций
Производные некоторых элементарных функций Форма прямоугольника
Форма прямоугольника Параллельность в пространстве
Параллельность в пространстве Анализ и изображение пространственных фигур
Анализ и изображение пространственных фигур Ромб, квадрат. Ответы на вопросы
Ромб, квадрат. Ответы на вопросы Геометрические фигуры (интерактивная игра)
Геометрические фигуры (интерактивная игра) Параллелограмм. Свойства параллелограмма. Трапеция
Параллелограмм. Свойства параллелограмма. Трапеция Объем наклонной призмы. Теорема
Объем наклонной призмы. Теорема Изображение пространственных фигур на плоскости
Изображение пространственных фигур на плоскости Решение уравнений третьей степени при подготовке к ЕГЭ
Решение уравнений третьей степени при подготовке к ЕГЭ Знаки тригонометрических функций. Формулы сложения
Знаки тригонометрических функций. Формулы сложения Карточки по математике. Состав числа
Карточки по математике. Состав числа Усеченная пирамида
Усеченная пирамида Лабораторная работа №1. Вычисление прямоугольных координат по геодезическим
Лабораторная работа №1. Вычисление прямоугольных координат по геодезическим Задачи на кратное сравнение
Задачи на кратное сравнение